Cheat sheet/zh-cn
From Kerbal Space Program Wiki
这一页面需要更新 请帮助Kerbal Space Program Wiki 更正 不准确或过时的信息.
|
坎巴拉太空计划的火箭科学家的参考手册:(Δv)表,方程和更多你可以参考的资料和笔记。
Contents
数学公式
推重比 (TWR)
- → See also: Thrust-to-weight ratio
基于牛顿第三定律,推重比小于1的航天器将无法从地面升空。推重比的计算涉及到航天器所处位置的重力加速度,且通常为天体表面的重力加速度。
Where:
- 是引擎推力
- 是航天器总质量
- 是航天器所受重力加速度 (通常为天体表面的重力加速度)
比冲 (Isp)
- → See also: Specific impulse
如果当前级的所有引擎的比冲都相等,则当前级的比冲为引擎的比冲,如果不相等,则参考下列公式计算:
速度增量 (Δv)
基本公式
- → See also: Tutorial:Advanced Rocket Design
基本的计算速度增量的公式,在大气层中使用大气层的比冲值而在真空中使用真空中的比冲值计算。
Where:
- 得出的速度增量单位为 m/s
- 起飞重量
- 燃料使用(喷)光之后的重量
- 飞行器的比冲
Δv 穿越大气层所需要的速度增量
| Body | Δvout |
|---|---|
| Kerbin | 1000 m/s |
| 其他星球数据未知 | |
计算火箭级的(Δv),考虑从大气向真空转变。Delta{v}_{out}是离开大气层所需的(Δv)量,不能达到轨道。 该方程可用于计算有大气层内发射到真空损耗的(Δv)
一些笔记
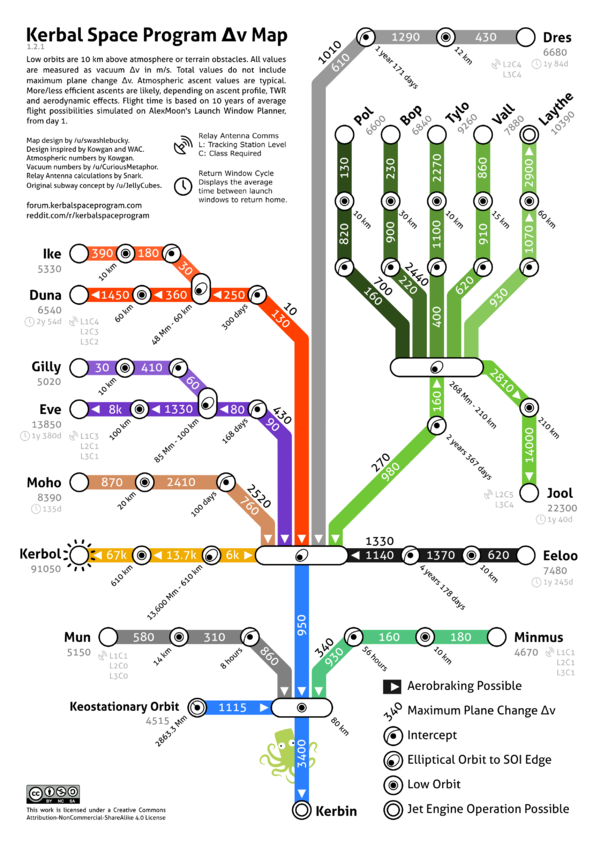
通过下面的章鱼图可以找到飞行器到目的轨道所需的速度增量.
Δv 的章鱼图 (KSP 1.2.1):
Total Δv values
Δv change values
Δv with Phase Angles
Precise Total Δv values
WAC's Δv Map for KSP 1.0.4
最大Δv 表
- 这张表格可以使你快速检索到每种引擎能到达的(Δv)的最大值(没有分级的情况下)
比冲(Vac) (s) 最大 Δv (m/s) 对应引擎 250 5394 O-10 "Puff" 290 6257 LV-1R "Spider"
24-77 "Twitch"300 6473 KR-1x2 "Twin-Boar" 305 6581 CR-7 R.A.P.I.E.R.
Mk-55 "Thud"310 6689 LV-T30 "Reliant"
RE-M3 "Mainsail"315 6797 LV-1 "Ant"
KS-25 "Vector"
KS-25x4 "Mammoth"320 6905 48-7S "Spark"
LV-T45 "Swivel"
RE-I5 "Skipper"340 7336 KR-2L+ "Rhino"
T-1 "Dart"345 7444 LV-909 "Terrier" 350 7552 RE-L10 "Poodle" 800 21837 LV-N "Nerv" 4200 33751 IX-6315 "Dawn"
(Version: 1.2.2)
数学举例
推重比
- 同上:
- TWR = F / (m * g) > 1
比冲
- 当所有引擎的比冲都相等时, 则当前级的比冲为引擎的比冲. 所以 六个比冲为200的引擎组成的引擎组,它们的比冲也是200.
- 如果不相等,则参考下列公式计算:
- 公式:
- 简化版:
- Isp = ( F1 + F2 + ... ) / ( ( F1 / Isp1 ) + ( F2 / Isp2 ) + ... )
- 解释:
- Isp = ( 第一台发动机推力 + 第二台发动机推力...等等... ) / ( ( 第一台发动机的推力 / 第一台发动机的比冲 ) + ( 第二台发动机的推力 / 第二台发动机的比冲 ) + ...第n台... )
- 举个栗子:
- 两个引擎,一号引擎200N推力120s比冲。二号引擎50N推力200s比冲.
- Isp = (200 N + 50 N) / ( ( 200 N / 120 s ) + ( 50 N / 200 s ) = 130.4347826 seconds
Δv
- 计算大气层中的速度增量使用大气层中的比冲值.
- 计算真空中的速度增量使用真空中的比冲值.
- 用下面的等式来计算每一级能获得的速度增量:
- 等式:
- 简写:
- Δv = ln ( Mstart / Mdry ) * 比冲 * g
- 解释:
- Δv = ln ( 起飞重量 / 燃料用光后重量 ) X Isp X 9.81
- 举例:
- 单级火箭起飞重量23t, 空重15t, 引擎比冲为120s.
- Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds Isp × 9.81m/s² = 总速度增量为 503.0152618 m/s
最大速度增量
- 最简单的计算方式为忽略除燃料罐(含燃料)之外的所有重量。
- 公式:
- 简化版:
- Δv =21.576745349086 * Isp
- 解释和例子:
- 这个公式中的常数是根据下ln(燃料罐满重、燃料罐空重)计算出来的,在燃料罐无线大时,其他组件的重量都可以被忽略.
- The following example will use a single stage and fuel tanks in the T-100 to Jumbo 64 range with an engine that outputs 380 seconds Isp.
- Δv = ln ( 18 Tons / 2 Tons ) × 380 seconds Isp × 9.81m/s² = Maximum Δv of 8199.1632327878 m/s
- Δv = 2.1972245773 × 380 seconds Isp × 9.82m/s² = Maximum Δv of 8199.1632327878 m/s (Replaced the log of mass with a constant as the ratio of total mass to dry mass is constant regardless of the number of tanks used as there is no other mass involved)
- Δv = 21.576745349086 × 380 seconds Isp = Maximum Δv of 8199.1632327878 m/s (Reduced to its most simple form by combining all the constants)
True Δv
- How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum.
- Assumption: It takes approximately 1000 m/s of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition.
- Note: This equation is an guess, approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate."
- Equation for Kerbin atmospheric escape:
- Simplified:
- True Δv = ( ( Δv atm - 1000 ) / Δv atm ) * Δv vac + 1000
- Explained:
- True Δv = ( ( Total Δv in atmosphere - 1000 m/s) / Total Δv in atmosphere ) X Total Δv in vacuum + 1000
- Example:
- Single stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum.
- Transitional Δv = ( ( 5000 Δv atm - 1000 Δv required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 1000 Δv required to escape Kerbin atmosphere = Total Δv of 5800 m/s