Terminology/ru
В KSP много понятий связано с физикой и небесной механикой, что может оказаться непривычным для непосвящённых. Кроме того разнообразные научные термины и аббревиатуры используются для описания общих понятий.
Данная статья составлена как краткий справочник по всей необходимой терминологии и призвана помочь Вам побыстрее стать настоящим кербонавтом!
Contents
Математические определения
- Эллиптический
- Овальной формы, часто в значении формы орбиты.
- Нормаль, вектор нормали
- Вектор, перпендикулярный к плоскости.
- Скаляр
- Величина, задающаяся одним числом, не имеет направления. Следующая за скаляром единица измерения указывает на его размерность, напр., 3 кг, 40 м, 15 с скалярные величины, обозначающие массу, расстояние и время соответственно. Скаляром является средняя путевая скорость.
- Вектор
- Характеризуется одновременно направлением и величиной. Форма записи зависит от используемой системы координат и числа измерений. <35°, 12> двумерный полярный вектор, а <14, 9, -20> трёхмерный декартовый вектор. Существуют и другие системы координат, но эти наиболее часто встречаются.
- <35°, 12> выглядит как стрела длиной 12 единиц, проведённая из начала координат (из нуля, где координата-угол значения не имеет, поскольку у этой точки длина отсутствует) в точку в 35° от координатной оси (обычно оси-Х, от которой положительные углы отсчитываются против часовой стрелки)
- <14, 9, -20> выглядит как стрела, проведённая из начала координат (<0,0,0>), в точку с координатой x = 14, координатой y = 9 и координатой z = -20.
- Преимущество использования декартовых координат в том, что сразу понятно расположение конечной точки, но труднее оценить длину, тогда как в полярных координатах длина задана явно, но зато сложнее представить положение.
- Следующие физические величины являются векторами: скорость (мгновенная), ускорение, сила
Для трёхмерной системы координат нужны:
- Точка/тело отсчёта.
- 3 базисных вектора. Они задают единицы измерения вдоль осей и ориентацию этих осей.
- Набор трёх скаляров, которые могут быть углами или линейными координатами, для задания положения в пространстве.
Орбиты
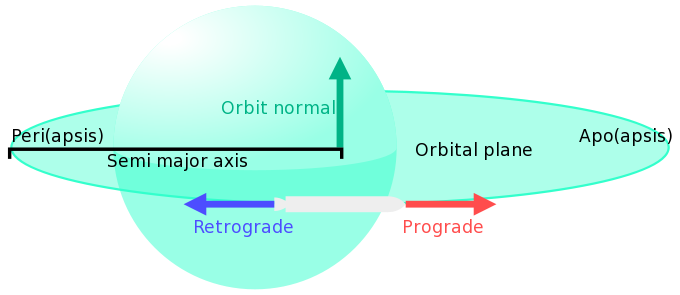
- Апсида
- Апсида (англ. "apsis") - это наиболее или наименее удалённая от притягивающего центра точка эллиптической орбиты небесного тела.
- Линия апсид
- Линия апсид - это прямая, связывающая две экстремальные точки (наиболее или наименее удалённую от притягивающего центра) эллиптической орбиты небесного тела - апсиды (от греч. hapsis, свод). Линия апсид совпадает с большой осью эллипса орбиты.
- Апоцентр
- Наиболее удалённая от центрального тела точка эллиптической орбиты.
- Перицентр
- Наиболее близкая к центральному телу точка эллиптической орбиты.
- Пери-* и Апо-*
- Нередко, когда идёт речь о конкретной орбите, корень "-центр" в словах "перицентр" и "апоцентр" заменяют на какое-нибудь слово, обозначающее конкретное небесное тело, напр., апогей, перигелий, апоселений. В данной же игре можно использовать -кей и -керб для описания орбит вокруг Кербина, получая таким образом Перикей/Перикерб и Апокей/Апокерб.
- Пери-* и Апо-*
- Линия апси́д — линия, соединяющая перицентр и апоцентр орбиты; для эллиптической орбиты линия апсид совпадает с большой осью эллипса и проходит также через фокус. Невозмущённая орбита симметрична относительно линии апсид.
- Базовая плоскость, начальная плоскость отсчёта
- Любая плоскость, используемая в качестве базовой для описания текущей орбиты. Для околопланетных орбит это часто плоскость экватора. В случае рассмотрения многих тел Солнечной системы применяется плоскость эклиптики. Для сближения с телом на другой орбите используется плоскость орбиты этого тела. Плоскость орбиты может быть полностью задана с помощью наклонения и долготы восходящего узла относительно плоскости отсчёта.
- Плоскость орбиты
- Воображаемая плоскость, в которой лежит орбита (применяются, напр., для описания наклонения).
- Узлы орбиты
- Точки пересечения плоскости орбиты с заданной базовой плоскостью или другими орбитами.
- Восходящий узел
- Точка, в которой орбита пересекает базовую плоскость при движении на север. Здесь, "север" означает направление нормали орбиты в базовой плоскости.
- Нисходящий узел
- Точка, в которой орбита пересекает базовую плоскость при движении на юг.
- Нормаль орбиты
- Нормальный вектор к плоскости орбиты. Получается векторным умножением скорости корабля на гравитацию. В связи с этим подчиняется правилу правой руки, если смотреть так, что корабль вращается против часовой стрелки, то вектор будет направлен вверх, если же корабль вращается по часовой, то вниз. Направление вектора часто обозначается как "Север" или "N+", а противоположный ему вектор обозначается как "анти-нормаль", "Юг" или "N-".
- Низкая опорная орбита (НОО)
- Понятие "низкая опорная орбита" применяется для многих планетоидов с гравитационной ямой, таких как Кербин. Оно описывает орбиту, которая низкая, но ещё устойчивая (над атмосферой). НОО используется как ступенька, после выхода на которую начинается перелёт к объекту назначения (к планете или другому аппарату), так как она позволяет произвести отлёт в любой удобной точке. Плюс в том, что требуется наименьшее количество топлива для выхода на НОО.
- Прогрейд
- Прогрейд (прямая орбита) -направление прямого движения по орбите. Соответствует касательной к орбите в точке, где в данный момент находится корабль.
- Ретрогрейд
- Ретрогрейд (обратная орбита) - противоположность прогрейду, направление, обратное прямому.
- Суборбитальный
- Описывает орбиту с перицентром под поверхностью планеты. Подобная траектория приведёт к столкновению с поверхностью.
- Сидери́ческий пери́од обраще́ния
- Сидери́ческий пери́од обраще́ния (от латинского "sidus" - звезда; "sideris") — промежуток времени, в течение которого какое-либо небесное тело-спутник совершает вокруг главного тела полный оборот относительно звёзд. Понятие «сидерический период обращения» применяется к обращающимся вокруг Земли телам — Луне (сидерический месяц) и искусственным спутникам, а также к обращающимся вокруг Солнца планетам, кометам и др. Сидерический период также называют годом. Например, Меркурианский год, Юпитерианский год, и т. п. При этом не следует забывать, что словом «год» могут называться несколько понятий. Так, не следует путать земной сидерический год (время одного оборота Земли вокруг Солнца) и год тропический (время, за которое происходит смена всех времён года), которые различаются между собой примерно на 20 минут (эта разница обусловлена, главным образом, прецессией земной оси).
- Синоди́ческий пери́од обраще́ния
- Синоди́ческий пери́од обраще́ния (англ. "Synodical period") (от греческого "σύνοδος" — соединение) — промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.
- → Смотрите также: Синодический период в Википедии.
Синодический период Луны равен промежутку времени между двумя новолуниями или двумя любыми другими одинаковыми последовательными фазами.
- Аномалистический период обращения
- Аномалистический период обращения — промежуток времени, за который тело, перемещаясь по эллиптической орбите, дважды последовательно проходит через перицентр.
- Малая полуось
- Малая полуось - это половина малой оси, перпендикулярной большой оси и проходящей через ее центральную точку, концы малой оси лежат на эллипсе.
Кеплеровы элементы орбиты
Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве в задаче двух тел: большая полуось - определяет размер орбиты, эксцентриситет - определяет форму орбиты, наклонение, аргумент перицентра и долгота восходящего узла - определяют положение орбиты в пространстве, истинная аномалия - определяет положение объекта на орбите относительно перицентра.
- Большая полуось
- Большая полуось (англ. "semi-major axis") (обозначается «a»)- это половина главной оси эллипса, в астрономии характеризует среднее расстояние небесного тела от фокуса. (определяет размер орбиты)
- Большая ось -- самая длинная ось эллипса, а большая полуось -- её половина. В KSP большая полуось рассчитывается как . Это среднее арифметическое апоцентра и перицентра, отсчитанных от центра выбранного тела. А поскольку оба они взяты как высоты от поверхности, то нужно добавить радиус. У всех орбит с равными большими полуосями -- равные периоды обращения, независимо от их эксцентриситета.
- Эксцентриситет
- Эксцентриситет (англ. "eccentricity") (обозначается «ε» или «e») — числовая характеристика конического сечения. Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия. Эксцентриситет характеризует «сжатость» орбиты.Это скаляр, описывающий отличие орбиты от окружности. (определяет форму орбиты)
- ecc = 0 → круговая орбита.
- 0 < ecc < 1 → эллиптическая орбита.
- ecc = 1 → параболическая орбита - это разомкнутая орбита убегания.
- ecc > 1 → гиперболическая орбита - это разомкнутая орбита убегания.
- Наклонение
- Наклонение (англ. "inclination") (обозначается «i») - угол между базовой плоскостью и плоскостью орбиты. (определяет положение орбиты в пространстве) Например, орбита с наклонением 90° к экватору называется полярной.
- Аргумент перицентра
- Аргумент перицентра или "аргумент широты" (англ. "argument of periapsis")(обозначается «ω» или «w») - определяется как угол между направлениями из притягивающего центра на восходящий узел орбиты и на перицентр (ближайшую к притягивающему центру точку орбиты спутника), или угол между линией узлов и линией апсид. (определяет положение орбиты в пространстве) Отсчитывается из притягивающего центра в направлении движения спутника, обычно выбирается в пределах 0°-360°. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидов вокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д.
- Долгота восходящего узла
- Долгота восходящего узла (англ. "longitude of the ascending node")(обозначается «Ω») - угол в базовой плоскости, образуемый между базовым направлением на нулевую точку и направлением на точку восходящего узла орбиты, в которой орбита пересекает базовую плоскость в направлении с юга на север. (определяет положение орбиты в пространстве) Это один из основных элементов орбиты, используемый для математического описания ориентации плоскости орбиты относительно базовой плоскости. Для тел, обращающихся вокруг звезды, базовая плоскость — эклиптика, а нулевая точка — точка весеннего равноденствия; угол измеряется от направления на нулевую точку против часовой стрелки.
- Истинная аномалия
- Средняя аномалия (англ. "true anomaly")(обозначается «ν») - угол между большой полуосью и лучом из фокуса на объект. (определяет положение объекта на орбите относительно перицентра)
Ориентация корабля
Ориентация корабля всегда задана относительно какого то объекта. Следующие термины обычно используются относительно кабины.
- Зенит
- Верхняя часть корабля, обычно направленна в противоположную сторону от тела на орбите которого находится корабль. Противоположный термин Надир.
- Надир
- Нижняя часть корабля, обычно направленна в сторону тела на орбите которого находится корабль. Противоположный термин Зенит.
- Бакборт(Левый борт)
- Левая сторона корабля. Противоположный термин Штирборт.
- Штирборт (Правый борт)
- Правая сторона корабля. Противоположный термин Бакборт.
- Нос
- Передняя сторона/конец корабля, направлена она в Прогрейд направлении. Противоположный термин Корма.
- Корма
- Задняя сторона/конец корабля, на ней обычно находятся основные двигатели, а направлена она в Ретрогрейд направлении. Противоположный термин Нос.
Космические манёвры
- Аэродинамическое торможение
- → Основная статья: Aerobraking/ru
- Достигается снижением высоты перицентра до верхних слоёв планетной атмосферы. Это вызовет торможение космического аппарата за счёт аэродинамического сопротивления. Может привести к вхождению в плотные слои и сходу с орбиты (см. ниже), но также применяется для сокращения необходимого времени работы двигателя при некоторых орбитальных манёврах.
- Зажигание
- Включение двигателей, как правило для изменения траектории.
- Скругление
- Манёвр, приводящий эксцентриситет орбиты к нулю или близко к нулю. Обычно выполняется включением двигателя возле апоцентра.
- Вход в атмосферу и спуск с орбиты
- Вход в атмосферу и использование сопротивления для торможения аппарата до пересекающейся с поверхностью траектории. Как правило вызывает интенсивный нагрев аппарата и требует определённого угла входа и скорости чтобы не "отскочить" от атмосферы обратно в космос. В текущей версии (0.20.2[outdated]) эффекты входа в атмосферу реализованы не полностью, без нагрева и "отскока". (Впрочем, присутствуют в модах)
- Тормозной импульс
- Импульс, направленный против орбитального движения, т.е. когда двигатели направлены по орбитальному движению, а нос корабля -- в противоположную сторону. Это обычный манёвр для снижения высоты орбиты без изменения других параметров орбиты.
- Тяговооружённость
- → Смотрите также: Thrust-to-weight ratio/ru
- Отношение между полной массой аппарата и располагаемой тягой всей двигательной установки аппарата/активной ступени. TWR > 1 означает, что аппарат обладает достаточной тягой чтобы взлететь. TWR менее 1 недостаточно для преодоления гравитации и движения на малой высоте, хотя низкая тяговооружённость может быть вполне достаточной в космосе. Потому что вес (W) аппарата зависит от ускорения свободного падения (g) в данной точке и TWR зависит от расположения аппарата. Сила тяжести на поверхности Муны составляет всего лишь 16.6 % от силы тяжести на Кербине, таким образом TWRKerbin = 1 превратится в TWRMun = 6.
Физика
- Траектория
- Траектория это линия, которую движущийся объект описывает в пространстве как функцию от времени.
- Баллистическая траектория
- Падающий объект движется по баллистической траектории. В ракетной технике это обычно означает, что рассматриваемый объект находится только под влиянием силы тяжести и не испытывает воздействия иных сил (т.е. нет силы тяги, аэродинамической подъёмной силы).
- Орбита
- → Основная статья: Orbit/ru
- Если объект обладает достаточной тангенциальной скоростью (и находится за пределами атмосферы, так что не тормозится из-за аэродинамического сопротивления), то он будет непрерывно падать на планету (никогда не достигая поверхности), то его траектория называется орбитой. Стабильны эллиптические орбиты (окружность есть эллипс с нулевым эксцентриситетом). Если тангенциальная скорость объекта превышает скорость убегания, то его орбита будет параболической или гиперболической.
- Мгновенная скорость
- Быстрота изменения координаты (положения). Является вектором, измеряется в "метрах в секунду" (м/с).
- Тангенциальная/касательная скорость
- Компонента скорости, касательная к траектории. Мгновенная скорость - скорость в отдельно взятый момент времени - всегда касательная к траектории.
- Ускорение
- Быстрота изменения скорости. Ускорение является вектором, измеряется в "м/с2".
- Характеристическая скорость (ΔV - Дельта-V)
- Максимальное приращение скорости, которое может произвести космический аппарат, зависит от количества топлива, эффективности двигателя, атмосферы, веса и гравитации. Измеряется в метрах в секунду (м/с). Увеличение массы аппарата снизит эту скорость, что потребует более мощного двигателя и большего количества топлива для достижения той же характеристической скорости. Это делает удобным использование этой величины для расчёта эффективности ракеты-носителя. Например, ракета должна иметь характеристическую скорость (Дельта-V) около 3500 м/с чтобы выйти за пределы атмосферы Кербина на низкую "парковочную" орбиту.
- По определению:
- где T - это тяга, m - это масса в данный момент
- Если внешние воздействующие силы отсутствуют и направление неизменно, то значение изменения скорости:
- В случае вычисления с удельным импульсом:
- Гравитация
- Универсальное взаимодействие между всеми материальными объектами. Очень слабое. Как правило очень массивные тела - т.е. планеты, луны - оказывают заметное воздействие. Убывает пропорционально квадрату расстояния от центра массы. Таким образом при удалении от гравитирующего объекта в два раза, сила притяжения составит 1/22 = 1/4 от изначальной.
- Гравитационная яма
- Область вокруг планеты с её гравитационным полем. Строго говоря, простирается до бесконечности, но, т.к. гравитация убывает пропорционально квадрату расстояния (если расстояние возрастает в 2 раза, то гравитация убывает в 4), то практический интерес представляет только в пределах сферы гравитационного влияния планеты.
- Гравитационная сфера, сфера гравитационного влияния
- → Основная статья: Sphere of influence/ru
- Область вокруг небесного тела, в пределах которой гравитацией небесного тела ещё нельзя пренебречь. В зависимости от задач выделяют разные сферы.
- Cфера тяготения – область пространства, внутри которой притяжение планеты превосходит солнечное тяготение.
- Сфера действия – область пространства, в которой при расчетах за центральное тело принимают планету, а не Солнце.
- Сфера Хилла – область пространства, в котором могут двигаться тела, оставаясь спутником планеты.
- Перегрузка (G)
- Отношение ускорения объекта к ускорению свободного падения на поверхности Земли. Измеряется в ускорениях свободного падения на поверхности Земли -- "G".
- К примеру если объект испытывает перегрузку в 4G - Значит на него "давит" сила равная четырём земным гравитациям, А на объект с ускорением в 1G будет "давить" сила равная земной силе притяжения.
- Сила притяжения
- Сила притяжения характеризуется ускорением свободного падения в гравитационном поле, и в случае Земли на уровне моря равно 9.81 м/с2. Это эквивалентно перегрузке в 1G.
- Первая космическая скорость (круговая скорость)
- Скорость, необходимая для круговой орбиты. Определяется как где G - гравитационная постоянная, M - масса планеты, и r - расстояние до центра притягивающего тела.
- Вторая космическая скорость (скорость убегания, параболическая скорость)
- Скорость, необходимая для преодоления гравитационной ямы рассматриваемой планеты и удаления на бесконечность, определяется как где G - гравитационная постоянная, M - масса планеты, и r - расстояние до центра притягивающего тела.
- Для полёта к луне бывает не обязательно разгоняться до 2й космической. Достаточно выйти на вытянутую эллиптическую орбиту с апоцентром, достигающим орбиту луны. Тем самым упрощается техническая задача и экономится топливо.
- Энергия (механическая)
- → Смотрите также: Specific orbital energy on Wikipedia
- Полная механическая энергия объекта на орбите складывается из потенциальной и кинетической энергий. Потенциальная энергия и кинетическая энергия где G - гравитационная постоянная, M - масса планеты, m - масса объекта, R -- расстояние до центра планеты и v - скорость. Таким образом . Если полная энергия тела отрицательна, то его траектория будет замкнутой, если равна или больше нуля, то параболической и гиперболической соответственно. Все орбиты с равными полуосями соответствуют равным энергиям.
- В этом и заключается основной смысл законов планетарного движения Кеплера, на основании которых и производится в "KSP" корректирование аппроксимация методом конических сечений. Эллипс - это набор всех точек на плоскости, расположенных таким образом, что сумма расстояний до двух точек - фокусов - является некоторой константой. Один из фокусов кеплеровской орбиты расположен в центре масс объекта, на орбите вокруг которого происходит движение; как только объект приближается к нему, то он обменивает потенциальную энергию на кинетическую энергию. Если объект движется от этого фокуса - эквивалентно, если орбита эллиптическая, поскольку объект приближается к другому фокусу - он обменивает кинетическую энергию на потенциальную энергию. Если летательный аппарат движется непосредственно к или от объекта, то фокусы совпадают с апсидами, в которых кинетическая (апоцентр) или потенциальная (перицентр) энергии нулевые. Если она идеально круглая (например орбита Муна вокруг Кербина), то два фокуса совпадают и расположение апсид не определено, так как каждая точка орбиты является апсидой.
- Также существует удельная орбитальная энергия (), которая не требует знания массы летательного аппарата для расчета: , , . Все орбиты с одинаковыми главными полуосями (a) имеют одинаковую удельную орбитальную энергию.
- Удельный импульс (Isp)
- → Основная статья: Specific impulse/ru
- Isp определяет эффективность реактивного двигателя. Чем выше Isp тем более мощной тягой обладает ракета при той же массе топлива. Isp часто даётся в секундах, но более физически корректная величина расстояние за время которая выражается в метрах в секунду или футах в секунду. Чтобы избежать путаницы с использованием этих величин, физически точную Isp (расстояние/время) делят на ускорение свободного падения на поверхности Земли (9.81 м/с2). И этот результат представляется в секундах. Чтобы использовать этот Isp в формулах, его нужно преобразовать обратно в расстояние за время что потребует снова умножения на ускорение свободного падения у поверхности Земли. А т.к. это ускорение используется только для взаимного преобразования данных двух величин, то удельный импульс не меняется при изменении гравитации. Похоже, что в "KSP" использовано значение 9.82 м/с2, что немного снижает расход топлива.
- Т.к. удельный импульс это отношение тяги к расходу топлива, то иногда его представляют в виде: . Математически это просто другая форма потому что сила это умножение массы на ускорение, по определению: . Таким образом, , что легко позволяет пользоваться основными единицами СИ.
Аэродинамика
- Предельная скорость падения
- → Основная статья: Terminal velocity/ru
Предельная скорость падения (англ. "Terminal velocity") - это скорость падения тела в газе или жидкости стабилизируется по достижении телом скорости, при которой сила гравитационного притяжения уравновешивается силой сопротивления среды. Более подробно о расчете предельной скорости в этой статье.
- Аэродинамическое сопротивление
- → Основная статья: Drag/ru
Аэродинамическое сопротивление (англ. "Drag") или "лобовое сопротивление" - это сила, с которой газ действует на движущееся в нём тело; эта сила направлена всегда в сторону, противоположную направлению скорости тела, и является одной из составляющих аэродинамической силы. Эта сила - результат необратимого перехода части кинетической энергии объекта в теплоту. Сопротивление зависит от формы и размеров объекта, ориентации его относительно направления скорости, а также от свойств и состояния среды, в которой объект движется. В реальных средах имеют место: вязкое трение в пограничном слое между поверхностью объекта и средой, потери на образование ударных волн при около- и сверхзвуковых скоростях движения (волновое сопротивление) и на вихреобразование. В зависимости от режима полёта и формы тела будут преобладать те или иные компоненты лобового сопротивления. Например, для затупленных тел вращения, движущихся с большой сверхзвуковой скоростью, оно определяется волновым сопротивлением. У хорошо обтекаемых тел, движущихся с небольшой скоростью - сопротивлением трения и потерями на вихреобразование. Разрежение, возникающее на задней торцевой поверхности обтекаемого тела, тоже приводит к возникновению результирующей силы, направленной противоположно скорости тела,— донного сопротивления, что может составлять значительную часть аэродинамического сопротивления. Более подробно о расчете аэродинамического сопротивления в этой статье.
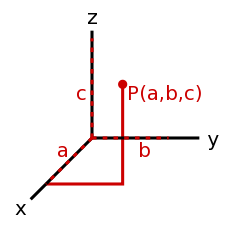
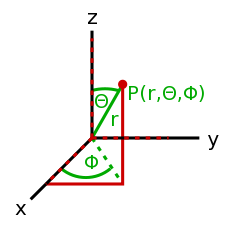
















![{\displaystyle [I_{sp}]={\frac {m}{s}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/072515563895cdf8f2d19f1dab433618230ce14f)



