Difference between revisions of "Cheat sheet"
From Kerbal Space Program Wiki
m (→Maps: *showing the image;) |
(reformat) |
||
| Line 1: | Line 1: | ||
Kerbal Space Program rocket scientist's '''cheat sheet''': Delta-v maps, equations and more for your reference so you can get from here to there and back again. | Kerbal Space Program rocket scientist's '''cheat sheet''': Delta-v maps, equations and more for your reference so you can get from here to there and back again. | ||
| − | == | + | = Mathematics = |
| − | === Delta-v (Δv) | + | == Thrust to weight ratio (TWR) == |
| − | === | + | {{See also|Terminology#TWR|Terminology}} |
| + | This is Newton's Second Law. If the ratio is less than 1 the craft will not lift off the ground. | ||
| + | |||
| + | <math>\text{TWR} = \frac{F}{m \cdot g}</math> | ||
| + | |||
| + | == Combined specific impulse (I<sub>sp</sub>) == | ||
| + | If the I<sub>sp</sub> is the same for all engines in a stage, then the I<sub>sp</sub> is equal to a single engine. If the I<sub>sp</sub> is different for engines in a single stage, then use the following equation: | ||
| + | |||
| + | <math>I_{sp} = \frac{(F_1 + F_2 + \dots)}{\frac{F_1}{I_{sp1}} + \frac{F_2}{I_{sp2}} + \dots}</math> | ||
| + | |||
| + | == Delta-v (Δv) == | ||
| + | ===Δv Basic calculation === | ||
{{See also|Tutorial:Advanced Rocket Design}} | {{See also|Tutorial:Advanced Rocket Design}} | ||
Basic calculation of a rocket's Δv. Use the atmospheric and vacuum thrust values for atmospheric and vacuum Δv, respectively. | Basic calculation of a rocket's Δv. Use the atmospheric and vacuum thrust values for atmospheric and vacuum Δv, respectively. | ||
| Line 9: | Line 20: | ||
<math>\Delta{v} = ln\left(\frac{M_{start}}{M_{end}}\right) \cdot I_{sp} \cdot 9.81 \frac{m}{s^2}</math> | <math>\Delta{v} = ln\left(\frac{M_{start}}{M_{end}}\right) \cdot I_{sp} \cdot 9.81 \frac{m}{s^2}</math> | ||
| − | + | === Transitional (true) Δv of a Stage that Crosses from Atmosphere to Vacuum === | |
{| class="wikitable" style="float:left;margin:0.5em;" | {| class="wikitable" style="float:left;margin:0.5em;" | ||
! Body !! Δv<sub>out</sub> | ! Body !! Δv<sub>out</sub> | ||
| Line 17: | Line 28: | ||
| other bodies' || data missing | | other bodies' || data missing | ||
|} | |} | ||
| − | Calculation of a rocket's Δv, taking | + | Calculation of a rocket stage's Δv, taking into account transitioning from atmosphere to vacuum. Δv<sub>out</sub> is the amount of Δv required to leave a body's atmosphere, ''not'' reach orbit. This equation is useful to figure out the actual Δv of a stage that ''transitions'' from atmosphere to vacuum. |
<math>\Delta{v}_T = \frac{\Delta{v}_{atm} - \Delta{v}_{out} \frac{m}{s^2}}{\Delta{v}_{atm}} \cdot \Delta{v}_{vac} + \Delta{v}_{out} \frac{m}{s^2}</math> | <math>\Delta{v}_T = \frac{\Delta{v}_{atm} - \Delta{v}_{out} \frac{m}{s^2}}{\Delta{v}_{atm}} \cdot \Delta{v}_{vac} + \Delta{v}_{out} \frac{m}{s^2}</math> | ||
{{clear|left}} | {{clear|left}} | ||
| − | + | === Maps === | |
| − | [[File:KerbinDeltaVMap.png | + | [[File:KerbinDeltaVMap.png|Δv to all bodies in the [[Kerbol System]]]] |
Various fan-made maps showing the Δv required to travel to a certain body. | Various fan-made maps showing the Δv required to travel to a certain body. | ||
| Line 33: | Line 44: | ||
* http://ubuntuone.com/1kD39BCoV38WP1QeG6MtO6 | * http://ubuntuone.com/1kD39BCoV38WP1QeG6MtO6 | ||
| − | == | + | = Math Examples = |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | + | ==TWR== |
| + | draft | ||
| + | ==(I<sub>sp</sub>)== | ||
| + | draft | ||
| + | ==(Δv)== | ||
| + | draft | ||
| − | + | = See also = | |
Links to collections of reference material. | Links to collections of reference material. | ||
* [[Tutorials]] | * [[Tutorials]] | ||
* [[Terminology]] | * [[Terminology]] | ||
* [[thread:28352|The Drawing Board: A library of tutorials and other useful information]] | * [[thread:28352|The Drawing Board: A library of tutorials and other useful information]] | ||
Revision as of 17:52, 3 July 2013
Kerbal Space Program rocket scientist's cheat sheet: Delta-v maps, equations and more for your reference so you can get from here to there and back again.
Contents
Mathematics
Thrust to weight ratio (TWR)
- → See also: Terminology
This is Newton's Second Law. If the ratio is less than 1 the craft will not lift off the ground.
Combined specific impulse (Isp)
If the Isp is the same for all engines in a stage, then the Isp is equal to a single engine. If the Isp is different for engines in a single stage, then use the following equation:
Delta-v (Δv)
Δv Basic calculation
- → See also: Tutorial:Advanced Rocket Design
Basic calculation of a rocket's Δv. Use the atmospheric and vacuum thrust values for atmospheric and vacuum Δv, respectively.
Transitional (true) Δv of a Stage that Crosses from Atmosphere to Vacuum
| Body | Δvout |
|---|---|
| Kerbin | 1000 m/s2 |
| other bodies' | data missing |
Calculation of a rocket stage's Δv, taking into account transitioning from atmosphere to vacuum. Δvout is the amount of Δv required to leave a body's atmosphere, not reach orbit. This equation is useful to figure out the actual Δv of a stage that transitions from atmosphere to vacuum.
Maps
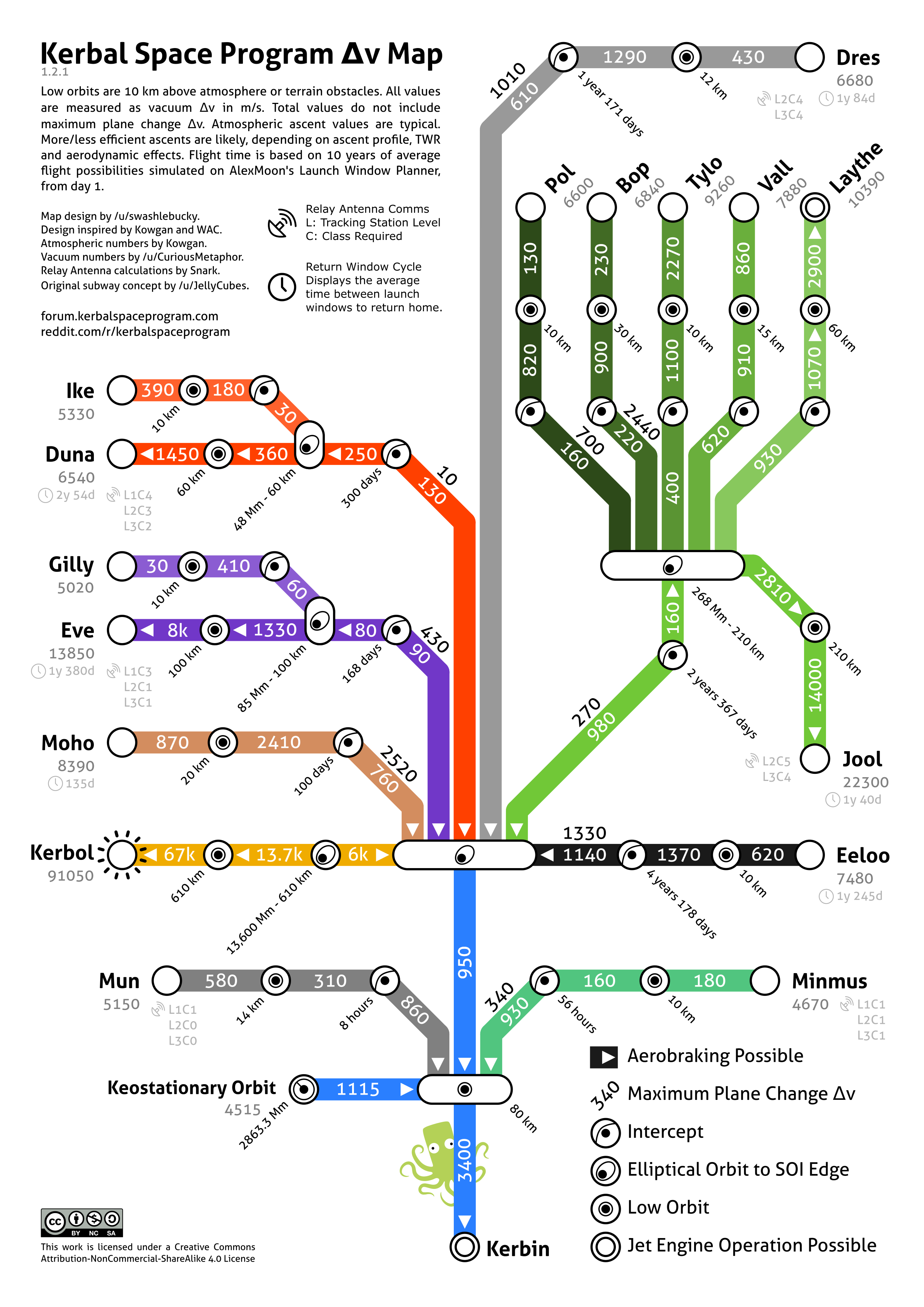Various fan-made maps showing the Δv required to travel to a certain body.
Total Δv values
Δv change values
Δv nomogram
Math Examples
TWR
draft
(Isp)
draft
(Δv)
draft
See also
Links to collections of reference material.
