Difference between revisions of "Cheat sheet"

Revision as of 21:26, 3 July 2013

Kerbal Space Program rocket scientist's cheat sheet: Delta-v maps, equations and more for your reference so you can get from here to there and back again.

Mathematics

Thrust to Weight Ratio (TWR)

→ See also: Terminology

This is Newton's Second Law. If the ratio is less than 1 the craft will not lift off the ground. Note that the local gravitational acceleration, which is usually the surface gravity of the body the rocket is starting from, is required.

${\displaystyle {\text{TWR}}={\frac {F}{m\cdot g}}>1}$

Where: ${\displaystyle F}$ is the thrust of the engines ${\displaystyle m}$ the total mass of the craft ${\displaystyle g}$ the local gravitational acceleration (usually surface gravity)

Combined Specific Impulse (I_sp)

If the I_sp is the same for all engines in a stage, then the I_sp is equal to a single engine. If the I_sp is different for engines in a single stage, then use the following equation:

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

Delta-v (Δv)

Basic calculation

→ See also: Tutorial:Advanced Rocket Design

Basic calculation of a rocket's Δv. Use the atmospheric and vacuum thrust values for atmospheric and vacuum Δv, respectively.

${\displaystyle \Delta {v}=ln\left({\frac {M_{start}}{M_{end}}}\right)\cdot I_{sp}\cdot 9.81{\frac {m}{s^{2}}}}$

True Δv of a stage that crosses from atmosphere to vacuum

Calculation of a rocket stage's Δv, taking into account transitioning from atmosphere to vacuum. Δv_out is the amount of Δv required to leave a body's atmosphere, not reach orbit. This equation is useful to figure out the actual Δv of a stage that transitions from atmosphere to vacuum.

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}{\frac {m}{s^{2}}}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}{\frac {m}{s^{2}}}}$

Maps

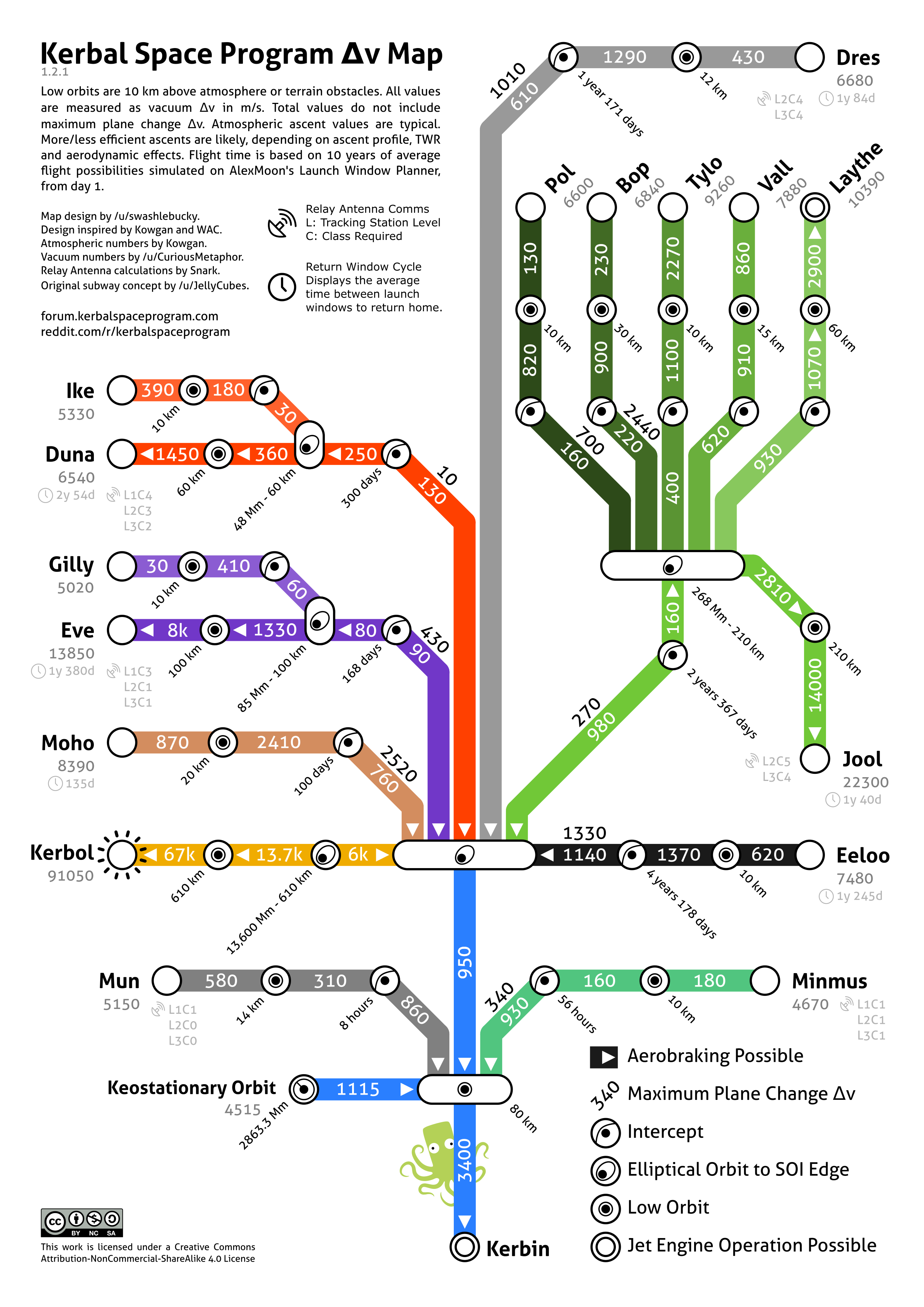Various fan-made maps showing the Δv required to travel to a certain body.

Total Δv values

• http://www.skyrender.net/lp/ksp/system_map.png

Δv change values

• http://i.imgur.com/duY2S.png

Δv nomogram

• http://ubuntuone.com/1kD39BCoV38WP1QeG6MtO6

Math examples

TWR

1. This is Newton's Second Law.
2. If the ratio is less than 1 the craft will not lift off the ground.

• Equation:

${\displaystyle {\text{TWR}}={\frac {F}{m\cdot g}}}$

• Simplified:

TWR = F / (m * g) > 1

• Explained:

TWR = Force of Thrust / ( Total Mass X 9.81 ) > 1

• Example:

200 kilonewton rocket engine on a 15 ton rocket launching from Kerbin Space Center.

TWR = 200 kN / ( 15 Tons total Mass X 9.81 m/s2 ) = 1.36 which is > 1 which means liftoff!

I_sp

1. When I_sp is the same for all engines in a stage, then the I_sp is equal to a single engine. So six 200 I_sp engines still yields only 200 I_sp.
2. When I_sp is different for engines in a single stage, then use the following equation:

• Equation:

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

• Simplified:

I_sp = ( F1 + F2 + ... ) / ( ( F1 / I_sp1 ) + ( F2 / I_sp2 ) + ... )

• Explained:

I_sp = ( Force of Thrust of 1st Engine + Force of Thrust of 2nd Engine...and so on... ) / ( ( Force of Thrust of 1st Engine / I_sp of 1st Engine ) + ( Force of Thrust of 2nd Engine / I_sp of 2nd Engine ) + ...and so on... )

• Example:

Two engines, one rated 200 newtons and 120 seconds I_sp ; another engine rated 50 newtons and 200 seconds I_sp.

Isp = (200 newtons + 50 newtons) / ( ( 200 newtons / 120 ) + ( 50 newtons / 200 ) = 130.89 seconds I_sp

Δv

1. For atmospheric Δv value, use atmospheric thrust values.
2. For vacuum Δv value, use vacuum thrust values.
3. Use this equation to figure out the Δv per stage:

• Equation:

${\displaystyle \Delta {v}=ln\left({\frac {M_{start}}{M_{dry}}}\right)\cdot I_{sp}\cdot 9.81{\frac {m}{s^{2}}}}$

• Simplified:

Δv = ln ( Mstart / Mdry ) * I_sp * g

• Explained:

Δv = ln ( Starting Mass / Dry Mass ) X Isp X 9.81

• Example:

Single Stage Rocket that weighs 23 tons when full, 15 tons when fuel is emptied, and engine that outputs 120 seconds I_sp.

Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds I_sp × 9.81m/s = Total Δv of 1803.2 m/s2

True Δv

1. How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum.
2. Assumption: It takes approximately 1000 m/s2 of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition.
3. Note: This equation is an guess, approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate."

• Equation for Kerbin Atmospheric Escape:

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}{\frac {m}{s^{2}}}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}{\frac {m}{s^{2}}}}$

• Simplified:

True Δv = ( ( Δv atm - 1000 ) / Δv atm ) * Δv vac + 1000

• Explained:

True Δv = ( ( Total Δv in atmosphere - 1000 m/s2) / Total Δv in atmosphere ) X Total Δv in vacuum + 1000

• Example:

Single Stage with total atmospheric Δv of 5000 m/s2, and rated 6000 Δv in vacuum.

Transitional Δv = ( ( 5000 Δv atm - 1000 Δv Required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 1000 Δv Required to escape Kerbin atmosphere = Total Δv of 5800 m/s2

See also

• Tutorials
• Terminology
• The Drawing Board: A library of tutorials and other useful information