Difference between revisions of "Atmosphere"
m (+pressures image; *rearranged the table with atmospheric bodies;) |
m (→Drag: *as drag coeff is weighted, the same part multiple times have the same coeff;) |
||
| Line 48: | Line 48: | ||
where p here is in units atm, and ''ρ'' in kg/m<sup>3</sup>. The 1.2230948554874 kg/m<sup>3</sup> value for density at 1 atmosphere (sea level on Kerbin) is given by [[API:FlightGlobals|FlightGlobals]].getAtmDensity(1.0). | where p here is in units atm, and ''ρ'' in kg/m<sup>3</sup>. The 1.2230948554874 kg/m<sup>3</sup> value for density at 1 atmosphere (sea level on Kerbin) is given by [[API:FlightGlobals|FlightGlobals]].getAtmDensity(1.0). | ||
| − | The coefficient of drag (''d'') is calculated as the mass-weighted average of the max_drag values of all [[parts]] on the ship. For most ships without deployed parachutes, ''d'' will be very near 0.2, since this is the max_drag value of the vast majority of parts. | + | The coefficient of drag (''d'') is calculated as the mass-weighted average of the max_drag values of all [[parts]] on the ship. For most ships without deployed parachutes, ''d'' will be very near 0.2, since this is the max_drag value of the vast majority of parts. Also a group of the same part have always the same drag coefficient. |
As an example, the coefficient of drag for a craft consisting simply of a [[Mk1-2 Command Pod]] (mass 4, drag 0.2) and a deployed [[Mk16-XL Parachute]] (mass 0.3, drag 500) is: | As an example, the coefficient of drag for a craft consisting simply of a [[Mk1-2 Command Pod]] (mass 4, drag 0.2) and a deployed [[Mk16-XL Parachute]] (mass 0.3, drag 500) is: | ||
Revision as of 17:38, 2 September 2013
| Planets | Moons | ||||
|---|---|---|---|---|---|
| |
Eve | |
Kerbin | |
Laythe |
| |
Duna | |
Jool | ||
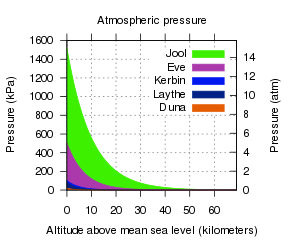
The atmosphere of a celestial body slows the movement of any object passing through it, a force known as atmospheric drag (or simply drag). An atmosphere also allows for aerodynamic lift. The celestial bodies with atmospheres are the planets Eve, Kerbin, Duna and Jool, as well as Laythe, a moon of Jool. Only Kerbin and Laythe have atmospheres that contain oxygen.
Atmospheric pressure diminishes exponentially with increasing altitude. An atmosphere's scale height is the distance over which atmospheric pressure changes as a factor of e, or 2.718. For example, Kerbin's atmosphere has a scale height of 5000 m, meaning the atmospheric pressure at altitude n is 2.718 times greater than the pressure at altitude n + 5000.
Atmospheres vary in temperature, though this has no bearing on gameplay.
Atmospheres allow aerobraking and easier landing. When an atmosphere contains oxygen, it allows jet engines to work. However, an atmosphere makes taking off from a planet more difficult and increases the minimum stable orbit altitude.
Drag
In the game, the force of atmospheric drag (FD) is modeled as follows:[1]
where ρ is the atmospheric density (kg/m3), v is the ship's velocity (m/s), d is the coefficient of drag (dimensionless), and A is the cross-sectional area (m2).
Note that the cross-sectional area is not actually calculated in the game. It is instead assumed that it is directly proportional to the mass, which is an unrealistic simplification made by KSP. The parameter FlightGlobals.DragMultiplier indicates that the proportionality ratio is 0.008 m2/kg, so:
where m is the ship's mass (kg).
The atmospheric density ρ is directly proportional to atmospheric pressure (p of unit atm), which is a function of altitude, the atmosphere's pressure at altitude 0 (p0), and scale height (H):
where p here is in units atm, and ρ in kg/m3. The 1.2230948554874 kg/m3 value for density at 1 atmosphere (sea level on Kerbin) is given by FlightGlobals.getAtmDensity(1.0).
The coefficient of drag (d) is calculated as the mass-weighted average of the max_drag values of all parts on the ship. For most ships without deployed parachutes, d will be very near 0.2, since this is the max_drag value of the vast majority of parts. Also a group of the same part have always the same drag coefficient.
As an example, the coefficient of drag for a craft consisting simply of a Mk1-2 Command Pod (mass 4, drag 0.2) and a deployed Mk16-XL Parachute (mass 0.3, drag 500) is:
Terminal velocity
The terminal velocity of an object falling through an atmosphere is the velocity at which the force of gravity is equal to the force of drag. Terminal velocity changes as a function of altitude. Given enough time, an object falling into the atmosphere will slow to terminal velocity and then remain at terminal velocity for the rest of its fall.
Terminal velocity is important because:
- It describes the amount of velocity which a spacecraft must burn away when it is close to the ground.
- It represents the speed at which a ship should be traveling upward during a fuel-optimal ascent.
The force of gravity (FG) is:
where m is still the ship's mass, G is the gravitational constant, M is the mass of the planet, and r is the distance from the center of the planet to the falling object.
To find terminal velocity, we set FG equal to FD:
Assuming d is 0.2 (which is a good approximation, provided parachutes are not in use), this simplifies to:
For the Mk16 pod and parachute example pictured above, the drag coefficient is 35.07, so its terminal velocity at sea level on Kerbin (which is 600 km from Kerbin's center) is:
Examples
| Altitude (m) | vT (m/s) | |||||
|---|---|---|---|---|---|---|
| Eve | Kerbin | Duna | Jool | Laythe | ||
| 0 | 58.385 | 100.13 | 212.41 | 23.124 | 115.62 | |
| 100 | 58.783 | 101.01 | 214.21 | 23.162 | 116.32 | |
| 1000 | 62.494 | 109.30 | 231.16 | 23.508 | 122.83 | |
| 10000 | 115.27 | 240.52 | 495.18 | 27.272 | 211.77 | |
On-rails physics
If a ship is "on rails" (meaning it's further than 2.25 km from the actively-controlled ship) and its orbit passes through a planet's atmosphere, one of two things will happen based on atmospheric pressure at the ship's altitude:
- below 0.01 atm: no atmospheric drag will occur — the ship will be completely unaffected
- 0.01 atm or above: the ship will disappear
The following table gives the altitude of this 0.01 atm threshold for each celestial body with an atmosphere:
| Body | Altitude (m) |
|---|---|
| Eve | 0 |
| Kerbin | 0 |
| Duna | 0 |
| Jool | 0 |
| Laythe | 0 |
Atmospheric height
The atmospheric height depend on the scale height of the celestial body and is where 0.000001th (0.0001 %) of the surface pressure is remaining so the atmospheric pressure at the border isn't constant. Technically a craft in Jool's orbit can get lower into the atmosphere (or the atmosphere starts from a higher pressure).
Kerbin's atmosphere ends at 0.000001 atm and to calculate where the other celestial bodies should have the atmospheric height: