Atmosphere
| Planets | Moons | ||||
|---|---|---|---|---|---|
| |
Eve | |
Kerbin | |
Laythe |
| |
Duna | |
Jool | ||
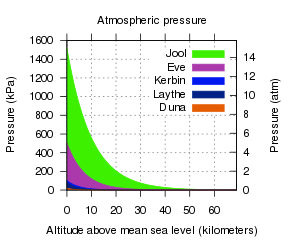
The atmosphere of a celestial body slows the movement of any object passing through it, a force known as atmospheric drag (or simply drag). An atmosphere also allows for aerodynamic lift. The celestial bodies with atmospheres are the planets Eve, Kerbin, Duna and Jool, as well as Laythe, a moon of Jool. Only Kerbin and Laythe have atmospheres that contain oxygen and thus produce intake air for jet engines to work.
Atmospheric pressure diminishes exponentially with increasing altitude. An atmosphere's scale height is the distance over which atmospheric pressure changes as a factor of e, or 2.718. For example, Kerbin's atmosphere has a scale height of 5000&nbs;m, meaning the atmospheric pressure at altitude n is 2.718 times greater than the pressure at altitude n + 5000.
Atmospheres vary in temperature, though this has no bearing on gameplay.
Atmospheres allow aerobraking and easier landing. However, an atmosphere makes taking off from a planet more difficult and increases the minimum stable orbit altitude.
Contents
Drag
In the game, the force of atmospheric drag is dependent on the shape of a part and which of the part's attachment nodes are in use. (For example, nose cones reduce drag on the part to which they are attached.) A debug-mode option allows you to see the exact drag force on a given part by right-clicking on it.
Generally the drag works as the following equation:
where ρ is the atmospheric density (kg/m3), v is the ship's velocity (m/s), d is the coefficient of drag (dimensionless), and A is the cross-sectional area (m2).
The atmospheric density ρ is directly proportional to atmospheric pressure (p of unit atm), which is a function of altitude, the atmosphere's pressure at altitude 0 (p0), and scale height (H):
where p here is in units atm, and ρ in kg/m3. The conversion factor of 1.2230948554874 kg/(m3·atm) is given by FlightGlobals.getAtmDensity(1.0), which returns the density at 1 atmosphere (sea level on Kerbin) pressure.
Atmospheric height
The atmospheric height depends on the scale height of the celestial body and is where 0.000001th (0.0001%) of the surface pressure remains. Therefore, the atmospheric pressure at the edge of the atmosphere is relative; for example a craft in orbit around Jool can have a lower orbit (relative to the surface) because the surface pressure is higher.
To calculate the atmospheric heights of other celestial bodies:
Terminal velocity
- → See also: terminal velocity on Wikipedia
The terminal velocity of an object falling through an atmosphere is the velocity at which the force of gravity is equal to the force of drag. Terminal velocity changes as a function of altitude. Given enough time, an object falling into the atmosphere will slow to terminal velocity and then remain at terminal velocity for the rest of its fall.
Terminal velocity is important because:
- It describes the amount of velocity which a spacecraft must burn away when it is close to the ground.
- It represents the speed at which a ship should be traveling upward during a fuel-optimal ascent.
The force of gravity (FG) is:
where m is still the ship's mass, G is the gravitational constant, M is the mass of the planet, and r is the distance from the center of the planet to the falling object.
To find terminal velocity, we set FG equal to FD:
Examples
The terminal velocity for an given imaginary body depends from the altitude on the different celestial bodies.
| Altitude (m) | vT (m/s) | |||||
|---|---|---|---|---|---|---|
| Eve | Kerbin | Duna | Jool | Laythe | ||
| 0 | 58.385 | 100.13 | 212.41 | 23.124 | 115.62 | |
| 100 | 58.783 | 101.01 | 214.21 | 23.162 | 116.32 | |
| 1000 | 62.494 | 109.30 | 231.16 | 23.508 | 122.83 | |
| 10000 | 115.27 | 240.52 | 495.18 | 27.272 | 211.77 | |
On-rails physics
A ship is "on rails" when it's no longer the primary focus of the simulation, which occurs when it's further than 2.25 km from the actively-controlled ship. If such a ship have its orbit passing through a planet's atmosphere, one of two things will happen based on atmospheric pressure at the ship's altitude:
- below 0.01 atm: no atmospheric drag will occur — the ship will be completely unaffected
- 0.01 atm or above: the ship will disappear
The following table gives the altitude of this 0.01 atm threshold for each celestial body with an atmosphere:
| Body | Altitude (m) |
|---|---|
| Eve | 44 745 |
| Kerbin | 25 789 |
| Duna | 10 814 |
| Jool | 219 397 |
| Laythe | 32 755 |