Difference between revisions of "Cheat sheet"
Kerik Balm (talk | contribs) m (→Maximum Δv chart: dV value for 345 Isp was wrong) |
(updated with newer delta-v map file from KSP forums) |
||
| (27 intermediate revisions by 17 users not shown) | |||
| Line 7: | Line 7: | ||
== Mathematics == | == Mathematics == | ||
| + | |||
=== Thrust-to-weight ratio (TWR) === | === Thrust-to-weight ratio (TWR) === | ||
| + | |||
{{See also|Thrust-to-weight ratio}} | {{See also|Thrust-to-weight ratio}} | ||
| − | + | ||
| + | How hard do your engines push UP? That's "thrust". | ||
| + | |||
| + | How hard does gravity pull DOWN? That's "weight". | ||
| + | |||
| + | The ratio of those two is, surprisingly, the "thrust-to-weight" ratio. | ||
| + | |||
| + | If thrust is pushing harder than weight, your rocket goes up! Hooray! | ||
| + | |||
| + | If weight is pulling harder than thrust, your rocket does not go up. Sad! | ||
| + | |||
| + | That's the "thrust-to-weight" ratio, or TWR, in a nutshell. | ||
{{Formula|math=\text{TWR} = \frac{F_T}{m \cdot g} > 1|where=* <math>F_T</math> is the thrust of the engines | {{Formula|math=\text{TWR} = \frac{F_T}{m \cdot g} > 1|where=* <math>F_T</math> is the thrust of the engines | ||
| Line 15: | Line 28: | ||
* <math>g</math> the local gravitational acceleration (usually surface gravity)}} | * <math>g</math> the local gravitational acceleration (usually surface gravity)}} | ||
| − | === | + | If TWR is less than one, then your rocket will not be going into space. You will need more engines, or perhaps MOAR BOOSTERZ! |
| + | |||
| + | If TWR is significantly above, say, 2.0, your rocket will ZOOM! But it might ZOOM too hard for your poor Kerbalnauts. Most rockets, straight off the launch pad, will utilize a TWR between 1.5 and 2.0. | ||
| + | |||
| + | === Specific Impulse (I<sub>sp</sub>) === | ||
| + | |||
{{See also|Specific impulse#Multiple engines|Specific impulse}} | {{See also|Specific impulse#Multiple engines|Specific impulse}} | ||
| − | |||
| − | + | Specific impulse measures the ''efficiency'' of a particular engine. Because this depends on the pressure of a rocket's surroundings, this can change between Sea Level and Vacuum (in space). Most engines are designed for optimal performance either at Sea Level (the big ones that drive your first stage and boosters, which have lots of thrust!) or Vacuum (where they won't burn as much propellant, but can be ''VERY'' efficient). | |
| + | |||
| + | Specific impulse is used in important equations like THE ROCKET EQUATION (see next section) to determine how much ''oomph'' (or "delta-vee") you can get out of a given amount of propellant. The higher the specific impulse, the more efficient an engine is! | ||
| + | |||
| + | In real life, specific impulse is governed by things like combustion chamber pressure and propellant energy (hydrogen/oxygen is more efficient than kerosene/oxgyen). Fortunately for Jebediah, our dear Kerbals only have one brand of fuel to worry about. | ||
=== Delta-v (Δv) === | === Delta-v (Δv) === | ||
| + | |||
==== Basic calculation ==== | ==== Basic calculation ==== | ||
{{See also|Tutorial:Advanced Rocket Design}} | {{See also|Tutorial:Advanced Rocket Design}} | ||
| Line 34: | Line 56: | ||
! Body !! Δv<sub>out</sub> | ! Body !! Δv<sub>out</sub> | ||
|- | |- | ||
| − | | [[Kerbin]] || | + | | [[Kerbin]] || 2500 m/s |
|- | |- | ||
| colspan="2" | other bodies' data missing | | colspan="2" | other bodies' data missing | ||
| Line 45: | Line 67: | ||
==== Maps ==== | ==== Maps ==== | ||
Various fan-made maps showing the Δv required to travel to a certain body. | Various fan-made maps showing the Δv required to travel to a certain body. | ||
| + | <br /> <br /> | ||
| + | |||
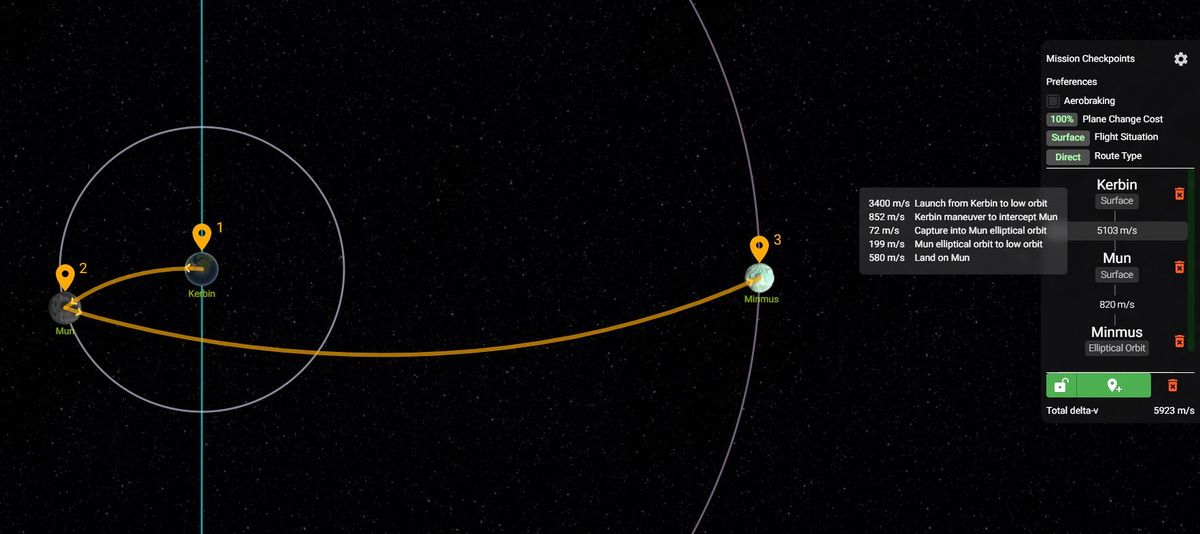
| + | '''KSP Visual Calculator, online tool that determines delta-v required for multiple checkpoint missions''' | ||
| + | * https://ksp-visual-calculator.blaarkies.com | ||
| + | [[File:Ksp-visual-calculator-map-dv-preview.jpg|1200px|Delta-v calculator]] | ||
| + | <br /> <br /> | ||
| + | |||
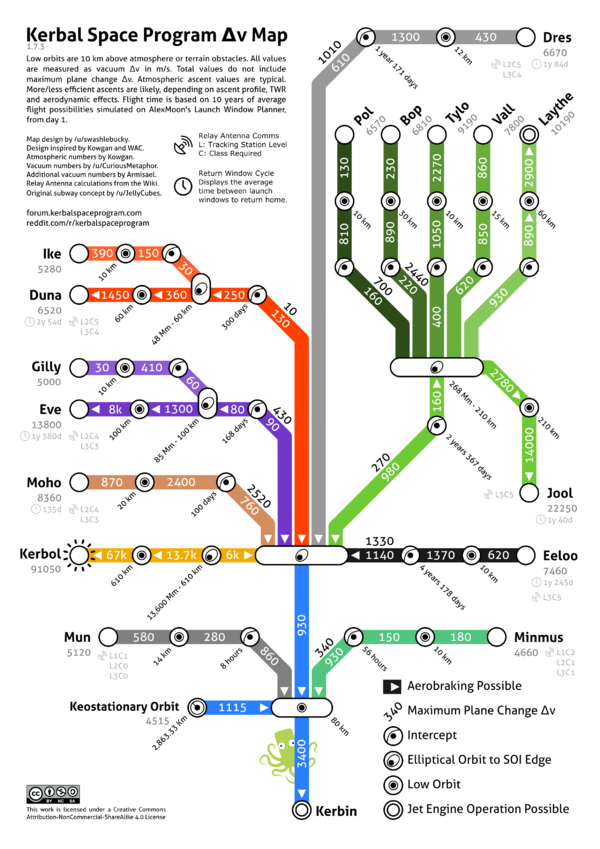
| + | '''Subway style Δv map ''(KSP 1.7.3)'':''' | ||
| + | [[File:Subwaydeltavmap1_7_3.png|center|600px|Δv to all bodies in the [[Kerbol System]]]] | ||
| + | <br /> <br /> | ||
| − | |||
| − | |||
'''Total Δv values''' | '''Total Δv values''' | ||
* http://www.skyrender.net/lp/ksp/system_map.png | * http://www.skyrender.net/lp/ksp/system_map.png | ||
| + | <br /> | ||
| + | |||
'''Δv change values''' | '''Δv change values''' | ||
* http://i.imgur.com/duY2S.png | * http://i.imgur.com/duY2S.png | ||
| + | <br /> | ||
| + | |||
'''Δv with Phase Angles''' | '''Δv with Phase Angles''' | ||
* http://i.imgur.com/dXT6r7s.png | * http://i.imgur.com/dXT6r7s.png | ||
| + | <br /> | ||
| + | |||
'''Precise Total Δv values''' | '''Precise Total Δv values''' | ||
* http://i.imgur.com/UUU8yCk.png | * http://i.imgur.com/UUU8yCk.png | ||
| + | <br /> | ||
| + | |||
| + | '''WAC's Δv Map for KSP 1.0.4''' | ||
| + | * http://i.imgur.com/q0gC9H7.png | ||
| + | <br /> | ||
==== Maximum Δv chart ==== | ==== Maximum Δv chart ==== | ||
| − | :This chart is a quick guide to what engine to use for a single stage interplanetary ship. No matter how much fuel you add you will never reach these ΔV without staging to shed mass or using the slingshot maneuver. | + | :This chart is a quick guide to what engine to use for a single stage interplanetary ship. No matter how much fuel you add you will never reach these ΔV without staging to shed mass or using the slingshot maneuver. (These calculations use a full/empty fuel-tank mass ratio of 9 for all engines except those noted.) |
:{| class="wikitable" | :{| class="wikitable" | ||
|- | |- | ||
| − | ! ISP (s) !! Max Δv (m/s) !! Engines | + | ! ISP(Vac) (s) !! Max Δv (m/s) !! Engines !! Remarks |
| + | |- | ||
| + | | 250 || 5249 || O-10 "Puff" || Monopropellant (max full/empty mass ratio = 8.5) | ||
|- | |- | ||
| − | | | + | | 290 || 6249 || LV-1R "Spider" <br /> 24-77 "Twitch" || |
|- | |- | ||
| − | | | + | | 300 || 6464 || KR-1x2 "Twin-Boar" || |
|- | |- | ||
| − | | | + | | 305 || 6572 || CR-7 R.A.P.I.E.R. <br /> Mk-55 "Thud" || |
|- | |- | ||
| − | | | + | | 310 || 6680 || LV-T30 "Reliant" <br /> RE-M3 "Mainsail" || |
|- | |- | ||
| − | | | + | | 315 || 6787|| LV-1 "Ant" <br /> KS-25 "Vector" <br /> KS-25x4 "Mammoth" || |
|- | |- | ||
| − | | | + | | 320 || 6895 || 48-7S "Spark" <br /> LV-T45 "Swivel" <br /> RE-I5 "Skipper" || |
|- | |- | ||
| − | | | + | | 340 || 7326 || KR-2L+ "Rhino" <br /> T-1 "Dart" || |
|- | |- | ||
| − | | | + | | 345 || 7434 || LV-909 "Terrier" || |
|- | |- | ||
| − | | | + | | 350 || 7542 || RE-L10 "Poodle" || |
|- | |- | ||
| − | | | + | | 800 || 17238 || LV-N "Nerv" || |
|- | |- | ||
| − | | | + | | 4200 || 58783 || IX-6315 "Dawn" || Xenon (max full/empty mass ratio = 4.167) |
|} | |} | ||
| − | (Version: 1. | + | (Version: 1.6.1) |
== Math examples == | == Math examples == | ||
| Line 109: | Line 152: | ||
*Example: | *Example: | ||
:Two engines, one rated 200 newtons and 120 seconds I<sub>sp</sub> ; another engine rated 50 newtons and 200 seconds I<sub>sp</sub>. | :Two engines, one rated 200 newtons and 120 seconds I<sub>sp</sub> ; another engine rated 50 newtons and 200 seconds I<sub>sp</sub>. | ||
| − | :Isp = (200 newtons + 50 newtons) / ( ( 200 newtons / 120 ) + ( 50 newtons / 200 ) = 130. | + | :Isp = (200 newtons + 50 newtons) / ( ( 200 newtons / 120 ) + ( 50 newtons / 200 ) = 130.4347826 seconds I<sub>sp</sub> |
=== Δv === | === Δv === | ||
| − | #For atmospheric Δv value, use atmospheric | + | #For atmospheric Δv value, use atmospheric <math>I_{sp}</math> values. |
| − | #For vacuum Δv value, use vacuum | + | #For vacuum Δv value, use vacuum <math>I_{sp}</math> values. |
#Use this equation to figure out the Δv per stage: | #Use this equation to figure out the Δv per stage: | ||
| Line 127: | Line 170: | ||
*Example: | *Example: | ||
:Single stage rocket that weighs 23 tons when full, 15 tons when fuel is emptied, and engine that outputs 120 seconds I<sub>sp</sub>. | :Single stage rocket that weighs 23 tons when full, 15 tons when fuel is emptied, and engine that outputs 120 seconds I<sub>sp</sub>. | ||
| − | :Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds I<sub>sp</sub> × 9.81m/s² = Total Δv of 503. | + | :Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds I<sub>sp</sub> × 9.81m/s² = Total Δv of 503.0152618 m/s |
=== Maximum Δv === | === Maximum Δv === | ||
| Line 145: | Line 188: | ||
=== True Δv === | === True Δv === | ||
#How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum. | #How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum. | ||
| − | #Assumption: It takes | + | #Assumption: It takes roughly 2500 m/s of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition (actual value ranges between 2000 m/s and 3400 m/s depending on ascent). Note that, as of KSP 1.3.1, around 3800 m/s of Δv is required to reach an 80km orbit from the KSC. |
| − | #Note: This equation is | + | #Note: This equation is a guess, an approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate." |
*Equation for Kerbin atmospheric escape: | *Equation for Kerbin atmospheric escape: | ||
| Line 153: | Line 196: | ||
*Simplified: | *Simplified: | ||
| − | ::'''True Δv = ( ( Δv atm - | + | ::'''True Δv = ( ( Δv atm - 2500 ) / Δv atm ) * Δv vac + 2500''' |
*Explained: | *Explained: | ||
| − | ::True Δv = ( ( Total Δv in atmosphere - | + | ::True Δv = ( ( Total Δv in atmosphere - 2500 m/s) / Total Δv in atmosphere ) X Total Δv in vacuum + 2500 |
*Example: | *Example: | ||
:Single stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum. | :Single stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum. | ||
| − | :Transitional Δv = ( ( 5000 Δv atm - | + | :Transitional Δv = ( ( 5000 Δv atm - 2500 Δv required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 2500 Δv required to escape Kerbin atmosphere = Total Δv of 5500 m/s |
== See also == | == See also == | ||
| Line 166: | Line 209: | ||
* [[Tutorials]] | * [[Tutorials]] | ||
* [[Terminology]] | * [[Terminology]] | ||
| − | * [[thread: | + | * [[thread:26220|The Drawing Board: A library of tutorials and other useful information]] |
Latest revision as of 08:54, 28 May 2022
This page or section is in need of being brought up to date. Please help Kerbal Space Program Wiki by fixing inaccurate or outdated information.
|
Kerbal Space Program rocket scientist's cheat sheet: Delta-v maps, equations and more for your reference so you can get from here to there and back again.
Contents
Mathematics
Thrust-to-weight ratio (TWR)
- → See also: Thrust-to-weight ratio
How hard do your engines push UP? That's "thrust".
How hard does gravity pull DOWN? That's "weight".
The ratio of those two is, surprisingly, the "thrust-to-weight" ratio.
If thrust is pushing harder than weight, your rocket goes up! Hooray!
If weight is pulling harder than thrust, your rocket does not go up. Sad!
That's the "thrust-to-weight" ratio, or TWR, in a nutshell.
- is the thrust of the engines
- the total mass of the craft
- the local gravitational acceleration (usually surface gravity)
If TWR is less than one, then your rocket will not be going into space. You will need more engines, or perhaps MOAR BOOSTERZ!
If TWR is significantly above, say, 2.0, your rocket will ZOOM! But it might ZOOM too hard for your poor Kerbalnauts. Most rockets, straight off the launch pad, will utilize a TWR between 1.5 and 2.0.
Specific Impulse (Isp)
- → See also: Specific impulse
Specific impulse measures the efficiency of a particular engine. Because this depends on the pressure of a rocket's surroundings, this can change between Sea Level and Vacuum (in space). Most engines are designed for optimal performance either at Sea Level (the big ones that drive your first stage and boosters, which have lots of thrust!) or Vacuum (where they won't burn as much propellant, but can be VERY efficient).
Specific impulse is used in important equations like THE ROCKET EQUATION (see next section) to determine how much oomph (or "delta-vee") you can get out of a given amount of propellant. The higher the specific impulse, the more efficient an engine is!
In real life, specific impulse is governed by things like combustion chamber pressure and propellant energy (hydrogen/oxygen is more efficient than kerosene/oxgyen). Fortunately for Jebediah, our dear Kerbals only have one brand of fuel to worry about.
Delta-v (Δv)
Basic calculation
- → See also: Tutorial:Advanced Rocket Design
Basic calculation of a rocket's Δv. Use the atmospheric and vacuum thrust values for atmospheric and vacuum Δv, respectively.
- is the velocity change possible in m/s
- is the starting mass in the same unit as
- is the end mass in the same unit as
- is the specific impulse of the engine in seconds
True Δv of a stage that crosses from atmosphere to vacuum
| Body | Δvout |
|---|---|
| Kerbin | 2500 m/s |
| other bodies' data missing | |
Calculation of a rocket stage's Δv, taking into account transitioning from atmosphere to vacuum. Δvout is the amount of Δv required to leave a body's atmosphere, not reach orbit. This equation is useful to figure out the actual Δv of a stage that transitions from atmosphere to vacuum.
Maps
Various fan-made maps showing the Δv required to travel to a certain body.
KSP Visual Calculator, online tool that determines delta-v required for multiple checkpoint missions
Subway style Δv map (KSP 1.7.3):
Total Δv values
Δv change values
Δv with Phase Angles
Precise Total Δv values
WAC's Δv Map for KSP 1.0.4
Maximum Δv chart
- This chart is a quick guide to what engine to use for a single stage interplanetary ship. No matter how much fuel you add you will never reach these ΔV without staging to shed mass or using the slingshot maneuver. (These calculations use a full/empty fuel-tank mass ratio of 9 for all engines except those noted.)
ISP(Vac) (s) Max Δv (m/s) Engines Remarks 250 5249 O-10 "Puff" Monopropellant (max full/empty mass ratio = 8.5) 290 6249 LV-1R "Spider"
24-77 "Twitch"300 6464 KR-1x2 "Twin-Boar" 305 6572 CR-7 R.A.P.I.E.R.
Mk-55 "Thud"310 6680 LV-T30 "Reliant"
RE-M3 "Mainsail"315 6787 LV-1 "Ant"
KS-25 "Vector"
KS-25x4 "Mammoth"320 6895 48-7S "Spark"
LV-T45 "Swivel"
RE-I5 "Skipper"340 7326 KR-2L+ "Rhino"
T-1 "Dart"345 7434 LV-909 "Terrier" 350 7542 RE-L10 "Poodle" 800 17238 LV-N "Nerv" 4200 58783 IX-6315 "Dawn" Xenon (max full/empty mass ratio = 4.167)
(Version: 1.6.1)
Math examples
TWR
- Copy template:
- TWR = F / (m * g) > 1
Isp
- When Isp is the same for all engines in a stage, then the Isp is equal to a single engine. So six 200 Isp engines still yields only 200 Isp.
- When Isp is different for engines in a single stage, then use the following equation:
- Equation:
- Simplified:
- Isp = ( F1 + F2 + ... ) / ( ( F1 / Isp1 ) + ( F2 / Isp2 ) + ... )
- Explained:
- Isp = ( Force of thrust of 1st engine + Force of thrust of 2nd engine...and so on... ) / ( ( Force of thrust of 1st engine / Isp of 1st engine ) + ( Force of thrust of 2nd engine / Isp of 2nd engine ) + ...and so on... )
- Example:
- Two engines, one rated 200 newtons and 120 seconds Isp ; another engine rated 50 newtons and 200 seconds Isp.
- Isp = (200 newtons + 50 newtons) / ( ( 200 newtons / 120 ) + ( 50 newtons / 200 ) = 130.4347826 seconds Isp
Δv
- For atmospheric Δv value, use atmospheric values.
- For vacuum Δv value, use vacuum values.
- Use this equation to figure out the Δv per stage:
- Equation:
- Simplified:
- Δv = ln ( Mstart / Mdry ) * Isp * g
- Explained:
- Δv = ln ( starting mass / dry mass ) X Isp X 9.81
- Example:
- Single stage rocket that weighs 23 tons when full, 15 tons when fuel is emptied, and engine that outputs 120 seconds Isp.
- Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds Isp × 9.81m/s² = Total Δv of 503.0152618 m/s
Maximum Δv
- Simplified version of the Δv calculation to find the maximum Δv a craft with the given ISP could hope to achieve. This is done by using a magic 0 mass engine and not having a payload.
- Equation:
- Simplified:
- Δv =21.576745349086 * Isp
- Explained / Examples:
- This calculation only uses the mass of the fuel tanks and so the ln ( Mstart / Mdry ) part of the Δv equation has been replaced by a constant as Mstart / Mdry is always 9 (or worse with some fuel tanks) regardless of how many fuel tanks you use.
- The following example will use a single stage and fuel tanks in the T-100 to Jumbo 64 range with an engine that outputs 380 seconds Isp.
- Δv = ln ( 18 Tons / 2 Tons ) × 380 seconds Isp × 9.81m/s² = Maximum Δv of 8199.1632327878 m/s
- Δv = 2.1972245773 × 380 seconds Isp × 9.82m/s² = Maximum Δv of 8199.1632327878 m/s (Replaced the log of mass with a constant as the ratio of total mass to dry mass is constant regardless of the number of tanks used as there is no other mass involved)
- Δv = 21.576745349086 × 380 seconds Isp = Maximum Δv of 8199.1632327878 m/s (Reduced to its most simple form by combining all the constants)
True Δv
- How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum.
- Assumption: It takes roughly 2500 m/s of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition (actual value ranges between 2000 m/s and 3400 m/s depending on ascent). Note that, as of KSP 1.3.1, around 3800 m/s of Δv is required to reach an 80km orbit from the KSC.
- Note: This equation is a guess, an approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate."
- Equation for Kerbin atmospheric escape:
- Simplified:
- True Δv = ( ( Δv atm - 2500 ) / Δv atm ) * Δv vac + 2500
- Explained:
- True Δv = ( ( Total Δv in atmosphere - 2500 m/s) / Total Δv in atmosphere ) X Total Δv in vacuum + 2500
- Example:
- Single stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum.
- Transitional Δv = ( ( 5000 Δv atm - 2500 Δv required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 2500 Δv required to escape Kerbin atmosphere = Total Δv of 5500 m/s