Difference between revisions of "Terminology/ko"
From Kerbal Space Program Wiki
Ysjbserver (talk | contribs) (→수학) |
Ysjbserver (talk | contribs) (→수학) |
||
| Line 12: | Line 12: | ||
* 위키 링크가 되지 않습니다. http://ko.wikipedia.org/wiki/%EB%B2%A1%ED%84%B0_(%EB%AC%BC%EB%A6%AC) | * 위키 링크가 되지 않습니다. http://ko.wikipedia.org/wiki/%EB%B2%A1%ED%84%B0_(%EB%AC%BC%EB%A6%AC) | ||
;Scalar | ;Scalar | ||
| − | : | + | :방향이 없는, 단일 값입니다. Scalars are usually followed by a unit of measurement that tells what the scalar's dimension is. eg 3 m/s, 3 m,3 s are scalar: they have units which denote speed, length/distance, and time respectively, but have no direction. |
;Vector | ;Vector | ||
:A set of a direction and a value. eg. heading (direction) and speed together give a velocity. How a vector is expressed depends on what the coordinate system is, and how many dimensions are taken into consideration. <35°, 12> is a two dimensional polar vector, where <14, 9, -20> is a three dimensional Cartesian vector. There are other coordinate systems but these are the most utilized. | :A set of a direction and a value. eg. heading (direction) and speed together give a velocity. How a vector is expressed depends on what the coordinate system is, and how many dimensions are taken into consideration. <35°, 12> is a two dimensional polar vector, where <14, 9, -20> is a three dimensional Cartesian vector. There are other coordinate systems but these are the most utilized. | ||
Revision as of 12:16, 6 March 2014
KSP에서 궤도에 관련된 말들은 종종 전문가가 아닌 사람들에게 혼동을 줄 수 있는, 물리학에 관련된 많은 용어가 있다. 또한, 다양한 다른 과학 용어 및 약어는 일반적인 용어를 설명하는 데 사용된다.
이 시트는 처음으로 하는 사람들이나 도움이 필요한 사람들에게 용어의 간결한 조회 테이블로 설계됨!
수학
- Elliptical
- 타원형 궤도를 나타냄
- Normal vector
- 표면에 수직인 벡터
- Scalar
- 방향이 없는, 단일 값입니다. Scalars are usually followed by a unit of measurement that tells what the scalar's dimension is. eg 3 m/s, 3 m,3 s are scalar: they have units which denote speed, length/distance, and time respectively, but have no direction.
- Vector
- A set of a direction and a value. eg. heading (direction) and speed together give a velocity. How a vector is expressed depends on what the coordinate system is, and how many dimensions are taken into consideration. <35°, 12> is a two dimensional polar vector, where <14, 9, -20> is a three dimensional Cartesian vector. There are other coordinate systems but these are the most utilized.
- <35°, 12> looks like an arrow which is 12 units long, starting from the origin (zero, angle does not matter because it is a point with no length) and ending at a point 35° from the base axis (typically the x-axis, positive angles progress counter-clockwise)
- <14, 9, -20> looks like an arrow starting from the origin (<0,0,0>) and ending at a point where the x coordinate is at 14, the y coordinate = 9 and the z coordinate = -20.
- The upside to using Cartesian coordinates is that you know exactly where the terminal position is, but it is more difficult to figure the length, however in polar coordinates it is trivial to find the length, the downside is its more difficult to know the position.
- The following physical qualities are all vectors: velocity, acceleration, force
A 3D coordinate systems needs:
- A point of reference. This is your origin.
- 3 base-vectors. These define your base unit of measurement along the axis and the direction of said axis.
- A mix of 3 scalars, that could be either angles or co-ordinates to express locations in your co-ordinate space.
Orbital Terms
- Apoapsis
- Periapsis
- Apsis
- → 참고하기: “Apoapsis and periapsis” section in Orbit
- Every elliptical orbit has two apsides. The periapsis (q) is at the closest point of the body being orbited (the lowest point in the orbit) and the apoapsis (Q) is on the other side of the orbit and is the farthest from the body being orbited (the highest point in the orbit). The apsides are usually given from the body's surface while most formula require the distance from the center of the body so the radius usually needs to get added.
- Peri-* and Apo-*
- When speaking of orbits, oftentimes the words "periapsis" and "apoapsis" will be modified to specify which planet or moon the orbit is around. For example, -kee and -kerb are both commonly used to describe orbits around Kerbin, resulting Perikee/Perikerb and Apokee/Apokerb.
- Ascending node
- The point at which the orbit crosses the reference plane moving north. Here, "north" means the direction of the orbit normal of the reference plane.
- Descending node
- The point at which the orbit crosses the reference plane moving south.
- Eccentricity
- A scalar describing how non-circular an orbit is.
- ecc = 0 → circular orbit.
- 0 < ecc < 1 → elliptical orbit.
- ecc = 1 → parabolic orbit - this is an escape orbit.
- ecc > 1 → hyperbolic orbit - this is an escape orbit.
- Inclination
- The angle between an orbital plane relative to a reference plane (e.g. an orbit with 90° inclination to an equatorial reference plane would be called polar).
- Low orbit
- An orbit that is only just high enough to indefinitely avoid succumbing to hazards of the body being orbited, such as atmospheric drag. Low orbits are used as stepstones, after ascent and before burning to another rendezvous object (planet or vessel), as it allows the exit burn to be performed in any direction and requires the least amount of fuel to reach from the body's surface. A low orbit for Kerbin is typically between 80km and 100km. Bodies with no atmosphere can theoretically allow an orbit at any height above the ground, but below 10km the risk of crashing into mountains or other elevated terrain becomes very high. The time warp is restricted to lower values while in low orbits.
- Orbital nodes
- Specific points of reference in any orbit such as Apoapsis, Periapsis, intersect points with other orbits etc.
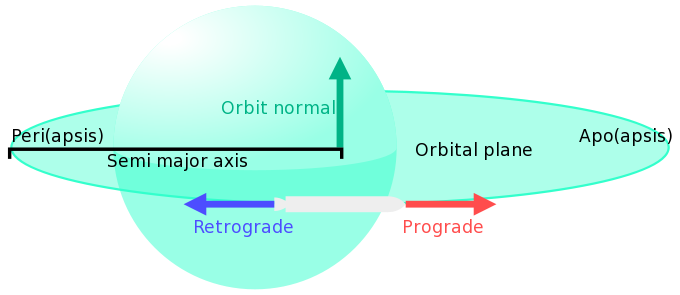
- Orbit normal
- A normal vector of the Orbital Plane. Produced by cross multiplying the ship's velocity and gravity. Since this follows the right hand rule, from a perspective where the ship is orbiting counter-clockwise it will point "up", while for a ship orbiting "clockwise" it will point down. "Up" is also often labeled as "North" or "N+", and in tandem with that "Down" is labeled "Anti-Normal", "South" or "N-".
- Orbital plane
- The imaginary disk described by the path of an orbit around a body (commonly used when describing inclinations).
- Prograde
- The direction in which a ship is traveling along its orbital path. Since orbits are elliptical, it is always tangent to the orbit at the point where the ship is.
- Retrograde
- The reverse of Prograde, backwards along the orbital path.
- Reference plane
- Any plane used as a reference for describing your current orbit. For local orbits around a planet, this is often the equatorial plane. When multiple bodies in a solar system are involved, the ecliptic plane can be used. For intercepting another orbiting body, the orbital plane of the body to be intercepted is used. An orbital plane can be fully described by giving the inclination and the longitude of the ascending node relative to a reference plane.
- Semi-major axis
- → 참고하기: “Semi-major axis” section in Orbit
- The major-axis is the long axis of an ellipse, and the semi-major axis (a) is half of this. It's the average of the apoapsis (Q) and periapsis (q) computed relative to the center of the body. As both are relative to the body's surface, the radius (R) must be added. All orbits with the same semi-major axis have the same period, regardless of their eccentricity.
- Sub-orbital
- Describes an orbit where the periapsis is below the surface of a planetary body. If a suborbital path is followed for too long the orbiter will collide with the body being orbited.
- Thrust-to-weight ratio
- → 참고하기: Thrust-to-weight ratio
- The Ratio between the total mass of the vehicle and the available thrust of all propulsion devices of the vehicle/current stage. A TWR greater than 1 means the craft will have enough thrust to accelerate vertically and gain altitude. A TWR below 1 means that the craft won't be able to counteract gravity and drag at low altitudes, although in space it only means that maneuvers will take longer. Because the weight (W) depends on the current gravitational acceleration (g) the TWR depends on which body is currently influencing the craft. The acceleration on the Mun's surface is only 16.6 % of Kerbin's acceleration, so at the surface a TWRKerbin = 1 would be a TWRMun = 6.
Ship Orientation
The ship orientation is always relative to a specific object. The terms are usually defined relative to the cockpit.
- Zenith
- Top side of the ship which is usually oriented away from the orbited body. Opposite of nadir.
- Nadir
- Bottom side of the ship which usually oriented towards the orbited body. Opposite of zenith.
- Port(side)
- Left side of the ship. Opposite of starboard.
- Starboard
- Right side of the ship. Opposite of portside.
- Front
- Front side/end of the ship which is usually towards the nose or prograde vector. Opposite of aft.
- Aft
- Back side/end of the ship which is usually housing the primary rockets and facing in retrograde. Opposite of front.
Space Maneuvers
- Atmospheric Braking
- → 원문 : Aerobraking
- Lowering the periapsis so it is inside a planetary atmosphere. This will lead to the vessel being slowed by atmospheric drag. Can lead to reentry (see below), but also is used to reduce the necessary burn time for significant orbit alterations.
- Atmospheric entry
- Entering atmosphere and using drag to decelerate a vessel to a groundwards trajectory. This usually causes intense heat stress on the object as the vessel requires sufficient speed to not "bounce" back from the atmosphere into space. Currently (0.22[outdated]) re-entry is only partially implemented with effects but heat and bounce are not yet implemented, there are mods however which allow parts to overheat. This is usually called re-entry/reentry but in theory only correct in Kerbin's atmosphere; atmospheric entry being the more general term.
- Burn
- firing of the engines, usually to alter trajectory in some way.
- Circularizing
- A maneuver (firing of the engines) that makes an orbit's eccentricity 0, or close to zero. This is usually achieved by a burn close to an apsis.
- Maneuver Node
- → 원문 : Maneuver node
- Maneuver nodes are a nice tool to plan and project trajectory changes in map view prior to doing the actual burn.
- Re-entry
- → 참고하기: Atmospheric entry
- Retroburn
- A burn performed "backwards", e.g. with the engines facing towards prograde and nose towards retrogade (hence the name). This is a common maneuver to used to lower the height of the orbit without altering any other orbital parameters.
Physics
- Acceleration
- Rate of change to the velocity. Acceleration is a vector, measured in "m/s2".
- Ballistic trajectory
- A falling object's trajectory is ballistic. In rocketry it usually indicates that the object in question is only influenced by gravity and does not exert any force (ie. thrust) of its own.
- Delta-v (Δv)
- The change in velocity that has or can be exerted by the spacecraft. This is measured in meters per second (m/s). More mass can reduce the delta-v, while more propulsion can increase it. This makes it a useful value to calculate the effectiveness of launch vehicles. For example, a launch vehicle requires about 4,500 m/s of delta-v to escape Kerbin's atmosphere and achieve a stable orbit.
- Energy
- → 참고하기: Specific orbital energy on Wikipedia
- The energy of an object in an orbit is the sum of its potential and kinetic energy. The potential energy is and kinetic energy where G is the gravitational constant, M is the mass of the body, m is the mass of the craft, R is the distance from the center of the body and v is the velocity. This results in . This sum stays the same when not thrusting: When approaching periapsis potential energy is transferred into kinetic energy. After passing the periapsis the kinetic energy is converted back into potential energy. When the energy or specific orbital energy is greater than zero the vehicle is on an escape trajectory.
- This is the basic idea behind Kepler's laws of planetary motion, which is what gives rise to KSP's patched conics approximation. An ellipse is the set of all points on a plane such that the sum of the distances to two points - the foci - is some constant. One focus of a Kepler orbit is the centre of mass of the object being orbited; as an object approaches it, it exchanges potential energy for kinetic energy. As the object moves away from this focus - equivalently, if the orbit is elliptical, as the object approaches the other focus - it exchanges kinetic energy for potential energy. If the craft going directly towards or away from the object, the foci coincide with the apsides, where the kinetic (apoapsis) or potential (periapsis) energy is zero. If it's perfectly circular (e.g. the Mun's orbit around Kerbin), the two foci coincide and the locations of the apsides are undefined, since every point of the orbit is an apsis.
- There is also the specific orbital energy () which doesn't require the mass of the craft: , , . All orbits with the same semi-major axis (a) have the same specific orbital energy.
- Escape Velocity
- The velocity needed to escape a given planet's gravity well, as given by where G is the gravitational constant, M is the mass of the planet, and r is the radius of the planet.
- g-force (G)
- A measurement of acceleration as expressed in the sea-level force of Earth's gravity with 1 G being about 9.81 m/s². An object at Earth's surface is accelerated at 1 G. The object weighs twice as much when at 2 G acceleration and is weightless when accelerated with 0 G. In free fall, like in orbit, and without an engine running or an atmosphere applying drag all objects experience no acceleration which can be expressed as 0 G.
- Gravity
- The force exerted by all objects with mass. Very weak. Usually only objects with very high mass - ie. planets, moons - have any noticeable effect. Diminishes with the square of distance from the center of mass. So for an object twice as far, experiences only 1/22 = 1/4 of the gravity.
- Gravity Well
- The area around a planet affected by gravity. Actually extends to infinity, but as gravity decreases quadratically with distance (after twice the distance the gravity is only a quarter), it is only significant within the body's sphere of influence. In fact, in KSP, gravity isn't simulated at all beyond a body's sphere of influence due to its use of the "patched conic approximation".
- Orbit
- → 원문 : Orbit
- When an object has sufficient tangential velocity (and is outside the atmosphere, so drag won't slow it down) so that it will keep falling "next" to the planet (never touching ground) its trajectory is called an orbit. Stable orbits are elliptical (a circle is an ellipse with zero eccentricity). If the objects tangential speed exceeds escape velocity it's orbit will be either para- or hyperbolic.
- Specific Impulse (Isp)
- → 원문 : Specific impulse
- The Isp defines how effective a propulsion system is. The higher the Isp the more powerful is the thrust applied to the rocket with the same fuel mass. The Isp is usually given in seconds but actually the physically correct unit is distance per time which is usually given in meters per second or feet per second. To avoid confusion which unit of speed is used, the physical correct Isp (in distance/time) is divided by the surface gravity of Earth (9.81 m/s²). This results in a value given in seconds. To use this Isp in formulas it must to be converted back into distance per time which requires multiplying with the surface gravity of Earth again. As this value is only used to convert between those two units, the specific impulse doesn't change when the gravity changes. It appears that KSP use a value like 9.82 m/s² and thus using a little less fuel.
- As the specific impulse is the ratio of thrust and fuel flow is sometimes given as the unit. This is mathematically another form of because force is the multiplication of mass and acceleration defining . So with the latter being simply only in SI base units.
- Sphere of influence
- The radius around a celestial body within which its gravity well is non-negligible. Commonly known as SoI/SOI.
- Tangential velocity
- The component of the velocity that is tangential to the trajectory. Instantaneous velocity - velocity when the time of measurement approaches zero - is always tangential to the trajectory.
- Trajectory
- A trajectory is the path that a moving object follows through space as a function of time.
- Velocity
- Rate of change of the position. It is the combination of speed with the direction. Velocity is a vector, measured in meters per second (m/s).











![I_{{sp}}={\frac {T}{{\dot m}}},[I_{{sp}}]={\frac {m}{s}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ff940eef93d9743a07d72ba2bb808e3b0372c36)



