Terminology/ko
From Kerbal Space Program Wiki
KSP에서 궤도에 관련된 말들은 종종 전문가가 아닌 사람들에게 혼동을 줄 수 있는, 물리학에 관련된 많은 용어가 있습니다. 또한, 다양한 다른 과학 용어 및 약어는 일반적인 용어를 설명하는 데 사용됩니다.
이 시트는 처음으로 하는 사람들이나 도움이 필요한 사람들에게 용어의 간결한 조회 테이블로 설계되었습니다!
수학
- Elliptical(타원형의)
- 타원형 궤도를 나타냅니다.
- Normal vector(표준 벡터)
- 표면에 수직인 벡터
- Scalar(스칼라)
- 방향이 없는, 단일 값입니다. 스칼라는 일반적으로 스칼라 차원이 무엇인지 알려줍니다. 예를 들자면, 3 미터/초, 3 미터,3 초는 스칼라입니다: 그들은 각각 속도, 거리 및 시간을 나타내는 단위가 있지만 방향이 없습니다.
- Vector(벡터)
- 방향의 설정 및 방향의 값을 나타냅니다. 예를 들어, 제목(방향)및 속도를 함께 보여줍니다. 벡터를 표현하는 방법의 좌표가 무엇인지에 따라, 많은 치수가 고려됩니다. <35°, 12> is a two dimensional polar vector, where <14, 9, -20> is a three dimensional Cartesian vector. There are other coordinate systems but these are the most utilized.
- <35°, 12> looks like an arrow which is 12 units long, starting from the origin (zero, angle does not matter because it is a point with no length) and ending at a point 35° from the base axis (typically the x-axis, positive angles progress counter-clockwise)
- <14, 9, -20> looks like an arrow starting from the origin (<0,0,0>) and ending at a point where the x coordinate is at 14, the y coordinate = 9 and the z coordinate = -20.
- The upside to using Cartesian coordinates is that you know exactly where the terminal position is, but it is more difficult to figure the length, however in polar coordinates it is trivial to find the length, the downside is its more difficult to know the position.
- The following physical qualities are all vectors: velocity, acceleration, force
A 3D coordinate systems needs:
- A point of reference. This is your origin.
- 3 base-vectors. These define your base unit of measurement along the axis and the direction of said axis.
- A mix of 3 scalars, that could be either angles or co-ordinates to express locations in your co-ordinate space.
Orbital Terms
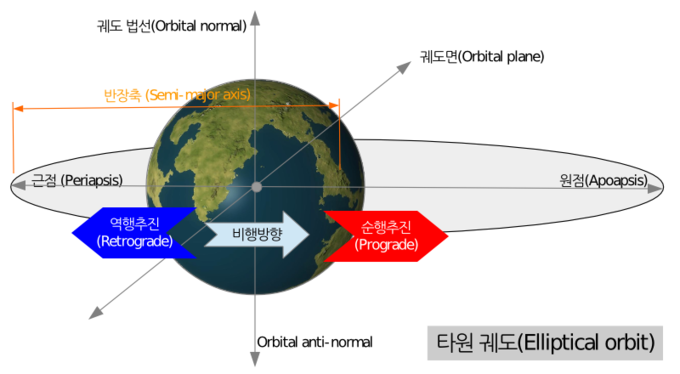
- 원점(遠點, 또는 원행점 遠行點) Apoapsis
- 지구를 궤도의 중심체(기준)로 하는 경우에는 원지점(遠地點), 태양을 기준으로 하는 경우에는 원일점(遠日點)이라 합니다.[참고: 천체물리학]
- 근점(近點, 또는 근행점 近行點) Periapsis
- 지구를 궤도의 중심체(기준)로 하는 경우에는 근지점(近地點), 태양을 기준으로 하는 경우에는 근일점(近日點)이라 합니다.[참고: 천체물리학]
- 장축단(長軸端) Apsis
- → 참고하기: “Apoapsis and periapsis” section in Orbit
- 모든 타원 궤도는 두개의 장축단을 가지고 있습니다. 근점(periapsis [Pe])은 궤도의 본체(중심체; 중심행성)에 가장 가까운 지점(궤도에서는 최저고도 지점)이고, 원점(apoapsis (Ap)은 반대로 가장 먼 지점(궤도에서는 최고고도 지점)입니다. 대부분의 공식(formula)은 본체(중심체) 중심에서부터의 거리를 필요로 하는데 반해, 장축단은 통상 본체(중심체)의 표면에서부터 얻어지므로 본체(중심체; 행성)의 반지름을 더한 값을 입력해야 합니다.
- 타원에는 두개의 지름(축)이 있는데, 긴 지름을 장축(長軸)이라하고 짧은 지름을 단축(短軸)이라 합니다. 반지름은 각각 반장축, 반단축이라 합니다. 장축단은 장축의 양 끝(端: 끝 단)을 의미하며, 타원의 중심에서 먼 끝을 최원점(Apogee)이라하고 가까운 끝을 최근점(Perigee)이라합니다. 천체물리학에서는 "Apogee"를 원지점(遠地點)이라 하고 "Perigee"를 근지점(近地點)이라 합니다. 참고로 원일점(遠日點)은 "aphelion", 근일점(近日點)은 "perihelion"이라 합니다. 어원은 모두 그리스어에서 유래되었습니다.[참고: 기하학, 천체물리학]
- 접두사 페리(Peri-*)와 애포(Apo-*)
- 그리스어에서 유래된 접두사 페리(Peri-)는 가까운(near)이라는 의미이며, 아포 또는 애포(Apo-)는 먼(away from)이라는 뜻입니다. 궤도와 관련하여 자주 언급되는 "근점(periapsis)"과 "원점(apoapsis)"은 종종 궤도의 중심이 되는 특정 행성이나 위성의 이름을 이용하여 고쳐 부르기도 합니다. 예를들어, "-kee"나 "-kerb"는 행성 커빈(Kerbin)의 주위를 도는 궤도에 사용되어 "Perikee/Perikerb" 또는 "Apokee/Apokerb"라고 부르기도 합니다.
- 승교점(昇交點, Ascending node)
- (공전)궤도가 수평 기준면(reference plane; 궤도의 중심천체가 갖는 수평면, 지구의 경우 적도, 태양의 경우 황도)을 북쪽 방향으로 교차하며 만나는 지점을 승교점이라고 합니다. 여기서 "북쪽"이라함은 수평 기준면에 대한 법선(orbit normal)방향을 말합니다.(그림: 궤도 도해 참조)
- 강교점(降交點, Descending node)
- (공전)궤도가 수평 기준면을 남쪽 방향으로 교차하며 만나는 지점을 강교점이라고 합니다.
- 이심률(離心率, Eccentricity)
- 궤도가 얼마나 원형에서 벗어났는가(찌그러졌는가)를 나타내는 스칼라값입니다.
- ecc = 0 → 원형 궤도.
- 0 < ecc < 1 → 타원형 궤도.
- ecc = 1 → 포물선 궤도 - 탈출 궤도.
- ecc > 1 → 쌍곡선 궤도 - 탈출 궤도.
- 궤도 경사각(傾斜角) Inclination
- 수평 기준면에 대한 궤도면(orbit plane; 위성체의 궤도가 이루는 수평면)의 기울기를 뜻합니다. 예를들어, 적도 기준면에 대하여 90°의 궤도 경사각을 갖는 위성궤도를 극궤도라고 합니다.
- 저궤도(Low orbit)
- An orbit that is only just high enough to indefinitely avoid succumbing to hazards of the body being orbited, such as atmospheric drag. Low orbits are used as stepstones, after ascent and before burning to another rendezvous object (planet or vessel), as it allows the exit burn to be performed in any direction and requires the least amount of fuel to reach from the body's surface. A low orbit for Kerbin is typically between 80km and 100km. Bodies with no atmosphere can theoretically allow an orbit at any height above the ground, but below 10km the risk of crashing into mountains or other elevated terrain becomes very high. The time warp is restricted to lower values while in low orbits.
- Orbital nodes
- Specific points of reference in any orbit such as Apoapsis, Periapsis, intersect points with other orbits etc.
- Orbit normal
- A normal vector of the Orbital Plane. Produced by cross multiplying the ship's velocity and gravity. Since this follows the right hand rule, from a perspective where the ship is orbiting counter-clockwise it will point "up", while for a ship orbiting "clockwise" it will point down. "Up" is also often labeled as "North" or "N+", and in tandem with that "Down" is labeled "Anti-Normal", "South" or "N-".
- Orbital plane
- The imaginary disk described by the path of an orbit around a body (commonly used when describing inclinations).
- Prograde
- The direction in which a ship is traveling along its orbital path. Since orbits are elliptical, it is always tangent to the orbit at the point where the ship is.
- Retrograde
- The reverse of Prograde, backwards along the orbital path.
- Reference plane
- Any plane used as a reference for describing your current orbit. For local orbits around a planet, this is often the equatorial plane. When multiple bodies in a solar system are involved, the ecliptic plane can be used. For intercepting another orbiting body, the orbital plane of the body to be intercepted is used. An orbital plane can be fully described by giving the inclination and the longitude of the ascending node relative to a reference plane.
- Semi-major axis
- → 참고하기: “Semi-major axis” section in Orbit
- The major-axis is the long axis of an ellipse, and the semi-major axis (a) is half of this. It's the average of the apoapsis (Q) and periapsis (q) computed relative to the center of the body. As both are relative to the body's surface, the radius (R) must be added. All orbits with the same semi-major axis have the same period, regardless of their eccentricity.
- Sub-orbital
- Describes an orbit where the periapsis is below the surface of a planetary body. If a suborbital path is followed for too long the orbiter will collide with the body being orbited.
- Thrust-to-weight ratio
- → 참고하기: Thrust-to-weight ratio
- The Ratio between the total mass of the vehicle and the available thrust of all propulsion devices of the vehicle/current stage. A TWR greater than 1 means the craft will have enough thrust to accelerate vertically and gain altitude. A TWR below 1 means that the craft won't be able to counteract gravity and drag at low altitudes, although in space it only means that maneuvers will take longer. Because the weight (W) depends on the current gravitational acceleration (g) the TWR depends on which body is currently influencing the craft. The acceleration on the Mun's surface is only 16.6 % of Kerbin's acceleration, so at the surface a TWRKerbin = 1 would be a TWRMun = 6.
Ship Orientation
The ship orientation is always relative to a specific object. The terms are usually defined relative to the cockpit.
- Zenith
- Top side of the ship which is usually oriented away from the orbited body. Opposite of nadir.
- Nadir
- Bottom side of the ship which usually oriented towards the orbited body. Opposite of zenith.
- Port(side)
- Left side of the ship. Opposite of starboard.
- Starboard
- Right side of the ship. Opposite of portside.
- Front
- Front side/end of the ship which is usually towards the nose or prograde vector. Opposite of aft.
- Aft
- Back side/end of the ship which is usually housing the primary rockets and facing in retrograde. Opposite of front.
Space Maneuvers
- Atmospheric Braking
- → 원문 : Aerobraking
- Lowering the periapsis so it is inside a planetary atmosphere. This will lead to the vessel being slowed by atmospheric drag. Can lead to reentry (see below), but also is used to reduce the necessary burn time for significant orbit alterations.
- Atmospheric entry
- Entering atmosphere and using drag to decelerate a vessel to a groundwards trajectory. This usually causes intense heat stress on the object as the vessel requires sufficient speed to not "bounce" back from the atmosphere into space. Currently (0.22[outdated]) re-entry is only partially implemented with effects but heat and bounce are not yet implemented, there are mods however which allow parts to overheat. This is usually called re-entry/reentry but in theory only correct in Kerbin's atmosphere; atmospheric entry being the more general term.
- Burn
- firing of the engines, usually to alter trajectory in some way.
- Circularizing
- A maneuver (firing of the engines) that makes an orbit's eccentricity 0, or close to zero. This is usually achieved by a burn close to an apsis.
- Maneuver Node
- → 원문 : Maneuver node
- Maneuver nodes are a nice tool to plan and project trajectory changes in map view prior to doing the actual burn.
- Re-entry
- → 참고하기: Atmospheric entry
- Retroburn
- A burn performed "backwards", e.g. with the engines facing towards prograde and nose towards retrogade (hence the name). This is a common maneuver to used to lower the height of the orbit without altering any other orbital parameters.
Physics
- Acceleration
- Rate of change to the velocity. Acceleration is a vector, measured in "m/s2".
- Ballistic trajectory
- A falling object's trajectory is ballistic. In rocketry it usually indicates that the object in question is only influenced by gravity and does not exert any force (ie. thrust) of its own.
- Delta-v (Δv)
- The change in velocity that has or can be exerted by the spacecraft. This is measured in meters per second (m/s). More mass can reduce the delta-v, while more propulsion can increase it. This makes it a useful value to calculate the effectiveness of launch vehicles. For example, a launch vehicle requires about 4,500 m/s of delta-v to escape Kerbin's atmosphere and achieve a stable orbit.
- Energy
- → 참고하기: Specific orbital energy on Wikipedia
- The energy of an object in an orbit is the sum of its potential and kinetic energy. The potential energy is and kinetic energy where G is the gravitational constant, M is the mass of the body, m is the mass of the craft, R is the distance from the center of the body and v is the velocity. This results in . This sum stays the same when not thrusting: When approaching periapsis potential energy is transferred into kinetic energy. After passing the periapsis the kinetic energy is converted back into potential energy. When the energy or specific orbital energy is greater than zero the vehicle is on an escape trajectory.
- This is the basic idea behind Kepler's laws of planetary motion, which is what gives rise to KSP's patched conics approximation. An ellipse is the set of all points on a plane such that the sum of the distances to two points - the foci - is some constant. One focus of a Kepler orbit is the centre of mass of the object being orbited; as an object approaches it, it exchanges potential energy for kinetic energy. As the object moves away from this focus - equivalently, if the orbit is elliptical, as the object approaches the other focus - it exchanges kinetic energy for potential energy. If the craft going directly towards or away from the object, the foci coincide with the apsides, where the kinetic (apoapsis) or potential (periapsis) energy is zero. If it's perfectly circular (e.g. the Mun's orbit around Kerbin), the two foci coincide and the locations of the apsides are undefined, since every point of the orbit is an apsis.
- There is also the specific orbital energy () which doesn't require the mass of the craft: , , . All orbits with the same semi-major axis (a) have the same specific orbital energy.
- Escape Velocity
- The velocity needed to escape a given planet's gravity well, as given by where G is the gravitational constant, M is the mass of the planet, and r is the radius of the planet.
- g-force (G)
- A measurement of acceleration as expressed in the sea-level force of Earth's gravity with 1 G being about 9.81 m/s². An object at Earth's surface is accelerated at 1 G. The object weighs twice as much when at 2 G acceleration and is weightless when accelerated with 0 G. In free fall, like in orbit, and without an engine running or an atmosphere applying drag all objects experience no acceleration which can be expressed as 0 G.
- Gravity
- The force exerted by all objects with mass. Very weak. Usually only objects with very high mass - ie. planets, moons - have any noticeable effect. Diminishes with the square of distance from the center of mass. So for an object twice as far, experiences only 1/22 = 1/4 of the gravity.
- Gravity Well
- The area around a planet affected by gravity. Actually extends to infinity, but as gravity decreases quadratically with distance (after twice the distance the gravity is only a quarter), it is only significant within the body's sphere of influence. In fact, in KSP, gravity isn't simulated at all beyond a body's sphere of influence due to its use of the "patched conic approximation".
- Orbit
- → 원문 : Orbit
- When an object has sufficient tangential velocity (and is outside the atmosphere, so drag won't slow it down) so that it will keep falling "next" to the planet (never touching ground) its trajectory is called an orbit. Stable orbits are elliptical (a circle is an ellipse with zero eccentricity). If the objects tangential speed exceeds escape velocity it's orbit will be either para- or hyperbolic.
- Specific Impulse (Isp)
- → 원문 : Specific impulse
- The Isp defines how effective a propulsion system is. The higher the Isp the more powerful is the thrust applied to the rocket with the same fuel mass. The Isp is usually given in seconds but actually the physically correct unit is distance per time which is usually given in meters per second or feet per second. To avoid confusion which unit of speed is used, the physical correct Isp (in distance/time) is divided by the surface gravity of Earth (9.81 m/s²). This results in a value given in seconds. To use this Isp in formulas it must to be converted back into distance per time which requires multiplying with the surface gravity of Earth again. As this value is only used to convert between those two units, the specific impulse doesn't change when the gravity changes. It appears that KSP use a value like 9.82 m/s² and thus using a little less fuel.
- As the specific impulse is the ratio of thrust and fuel flow is sometimes given as the unit. This is mathematically another form of because force is the multiplication of mass and acceleration defining . So with the latter being simply only in SI base units.
- Sphere of influence
- The radius around a celestial body within which its gravity well is non-negligible. Commonly known as SoI/SOI.
- Tangential velocity
- The component of the velocity that is tangential to the trajectory. Instantaneous velocity - velocity when the time of measurement approaches zero - is always tangential to the trajectory.
- Trajectory
- A trajectory is the path that a moving object follows through space as a function of time.
- Velocity
- Rate of change of the position. It is the combination of speed with the direction. Velocity is a vector, measured in meters per second (m/s).
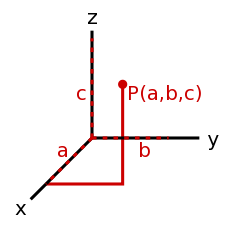
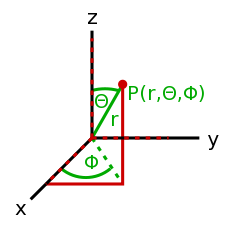











![I_{{sp}}={\frac {T}{{\dot m}}},[I_{{sp}}]={\frac {m}{s}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ff940eef93d9743a07d72ba2bb808e3b0372c36)



