Tutorial: Basic Orbiting (Technical)/zh-cn
进入太空相对还算容易,但能停留在那里,而不是一路飘向无尽的宇宙,或者落回到 Kerbin,这就有一定的挑战性了。本指南希望能帮助你进入并停留在轨道上(orbit),还有如何把轨道调整为圆形或者椭圆形,以及如何调节轨道的高度。
The force acting on one of the masses m by the other two is:
This acts as the centripetal force and hence
and hence,
T = 4 ? R ^ (3/2) / ?{ G [4 M + m]}
Contents
轨道稳定
在每个轨道周期中,飞行器的高度变化都会有一个最高值,即到达轨道远点;并在其对侧面飞抵高度最低点,即轨道近点。位于轨道远点和近点时,飞行器的垂直分量速度为零。这两个点是最容易对轨道进行调整的位置,由于这是垂直速度为零,你能够轻松的调整速度的大小。注: 轨道远点和近点的差别就是离心率。离心率为零,该轨道就是圆形轨道,长椭圆形的轨道离心率接近 1。
There are a number of third-party calculators available which can crunch the numbers and tell you your eccentricity, as well as provide the speeds required to circularize your orbit at your current (or future) altitude. Whether you calculate your orbits by hand, or use a third party app, the general procedures are still the same and are given below:
First, in order to get into a nice, round orbit, you need to determine how fast to go. The higher your orbit, the less gravity you'll feel from Kerbin, so the slower you'll need to go to be in a circular orbit. Consult the table below, or use a 3rd party table, to determine the proper speed for your altitude at apoapsis or periapsis. You'll probably want to watch your altimiter as you near one of the critical points, remember the altitude, look up the speed in the table, and make the correction on your next pass. If you want to "round out" your orbit from apoapsis, you need to speed up to avoid falling back down to periapsis. Point your craft in the exact direction of travel (use the green circular indicator on the gimbal to line up), and apply thrust until you've gained enough speed. To round out an orbit from periapsis, you need to slow down to avoid climbing back up to apoapsis. Point your craft in the opposite direction of travel (indicated on the gimbal by a green circle with an "X" through it), and apply thrust until you have slowed to the speed indicated by the table. You should then be in an orbit that is very close to circular! Depending on how eccentric your initial orbit was, you may need to make a large correction on your first pass followed by a small correction on a subsequent pass to get very stable.
If you have version 0.11 or better, adding a set of RCS thrusters to your craft can help make minute adjustments to an orbit easier. Version 0.11 also allows you to see the current trajectory (and read periapsis and apoapsis altitudes) by switching to the Map view (M key)
Transfer Orbits
The most efficient way to transfer from a lower circular orbit to a higher circular orbit (or vice-versa) is to use an elliptical transfer orbit, also known as a Hohmann transfer orbit. To transfer, we make the periapsis of the elliptical orbit the same as the radius of the lower orbit, and the apoapsis of the elliptical orbit the same as the radius of the higher orbit. If you are going from low to high, you make a burn in the direction of travel to elongate your orbit. You will climb in altitude as you travel around the planet to the apoapsis of your transfer orbit. Then, make a second burn to round out the new, higher orbit (as described above). To go from high to low, do the opposite: Burn in the opposite direction of travel, then fall down to the periapsis of your transfer orbit, and make a second burn to round out the lower orbit (again in the opposite direction of travel).
Target Speed
The key to transfer orbits is figuring out how much speed to add or subtract to reach a desired new orbital altitude. To do this, use the formula below to determine the target velocity for your initial burn:
In this formula, rl and rh are the radii of the lower and higher orbits, respectively, and ri is the radius of the initial orbit. If you are transferring to a higher orbit, ri will be equal to rl, and v will be faster than your current speed, so burn in the direction of travel to reach v. If you are transferring to a lower orbit, ri will be equal to rh, and v will be slower than your current speed, so burn in the opposite direction to reach v. Remember, v is the target speed for your initial burn that puts you into the elliptical transfer orbit. Once you reach your new orbital altitude, you need to make a second burn to round out your orbit, using the same technique described in the stabilizing your orbit section.
Details of where this formula comes from are in the technical section below. When using this formula, take care to remember that the radius of an orbit is equal to the orbital altitude plus Kerbin's radius (600 000 m).
De-orbiting
The most efficient way to de-orbit from any altitude is to initiate a transfer orbit with a periapsis below 70000 m, the edge of Kerbin's atmosphere. Note that the upper atmosphere is very thin so if you do not want to wait for several orbits of aerobraking, aim for under 35000 m and thicker air. As you approach periapsis, the atmospheric drag will start to slow your craft and eventually it can no longer maintain orbit.
R code snippet for planning Hohmann transfer
hohmann <- function(from_alt,to_alt){
# provides information needed to perform
# a hohmann transfer from a circular ortbit
# at from_alt (km) to a circular orbit at to_alt (km)
mu <- 3530.394 # Gravitational parameter (km^3/s^2)
R <- 600 # Kerbin radius (km)
r1 <- from_alt+R # radius 1 (km)
r2 <- to_alt+R # radius 2 (km)
vc1 <- sqrt(mu/r1) # circular orbit velocity 1 (km/s)
vc2 <- sqrt(mu/r2) # circular orbit velocity 2 (km/s)
a <- (r1+r2)/2 # semi-major axis of transfer orbit (km)
T <- 2*pi*sqrt((a^3)/mu) # period of transfer orbit (s)
dv1 <- (sqrt(r2/a)-1)*vc1 # delta v1 (km/s)
dv2 <- (1-sqrt(r1/a))*vc2 # delta v2 (km/s)
b1 <- list(from=vc1,to=vc1+dv1) # burn one from-to velocities (km/s)
t <- T/2 # time between burns (s)
b2 <- list(from=vc2+dv2,to=vc2) # burn two from-to velocities (km/s)
out <- list(from_alt=from_alt,b1=b1,t=t,b2=b2,to_alt=to_alt)
return(out)}
Example usage
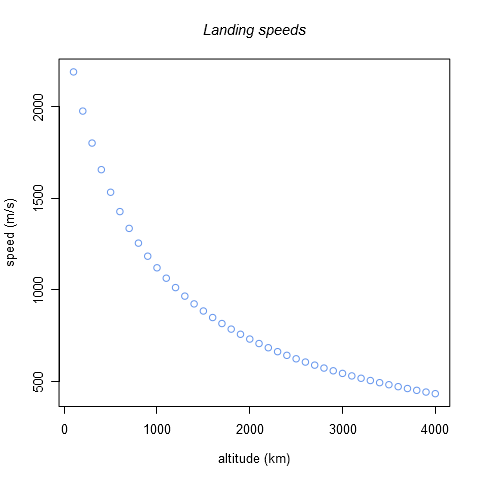
Produce a graph showing the speeds need to transfer from a range of circular orbit altitudes into a landing orbit.
plot(100*1:40,1000*hohmann(100*1:40,34)$b1$to,main="Landing speeds",xlab="altitude (km)",ylab="speed (m/s)")
R project Link[1]
Transfer Orbits
Coming soon!
Orbital Table
Note: The atmosphere previously had a sharp cutoff at 34.5 km, but now extends to approximately 68 km. Below this altitude, your orbit will gradually decay. The decay becomes quite rapid below about 45 km. The orbital parameters below 68 km are provided for reference, but understand that you will not be able to maintain these orbits without regular corrections to counteract the atmospheric drag.
| Altitude (m) | Horizontal Speed (m/s) | Orbital Period (min) |
|---|---|---|
| 40000 | 2348.7 | 28.54 |
| 50000 | 2330.6 | 29.21 |
| 60000 | 2312.8 | 29.88 |
| 70000 | 2295.5 | 30.56 |
| 80000 | 2278.6 | 31.25 |
| 85000 | 2270.3 | 31.60 |
| 90000 | 2262.0 | 31.94 |
| 100000 | 2245.8 | 32.64 |
| 110000 | 2229.9 | 33.34 |
| 120000 | 2214.4 | 34.05 |
| 130000 | 2199.2 | 34.76 |
| 140000 | 2184.3 | 35.48 |
| 150000 | 2169.6 | 36.20 |
| 160000 | 2155.3 | 36.93 |
| 170000 | 2141.3 | 37.66 |
| 180000 | 2127.5 | 38.39 |
| 190000 | 2114.0 | 39.13 |
| 200000 | 2100.7 | 39.88 |
| 210000 | 2087.7 | 40.63 |
| 220000 | 2075.0 | 41.38 |
| 230000 | 2062.4 | 42.14 |
| 240000 | 2050.1 | 42.91 |
| 250000 | 2038.0 | 43.68 |
| 260000 | 2026.1 | 44.45 |
| 270000 | 2014.5 | 45.23 |
| 280000 | 2003.0 | 46.01 |
| 290000 | 1991.7 | 46.79 |
| 300000 | 1980.6 | 47.59 |
| 310000 | 1969.7 | 48.38 |
| 320000 | 1959.0 | 49.18 |
| 330000 | 1948.4 | 49.98 |
| 340000 | 1938.0 | 50.79 |
| 350000 | 1927.8 | 51.61 |
| 360000 | 1917.7 | 52.42 |
| 370000 | 1907.8 | 53.24 |
| 380000 | 1898.0 | 54.07 |
| 390000 | 1888.4 | 54.90 |
| 400000 | 1879.0 | 55.73 |
| 410000 | 1869.6 | 56.57 |
| 420000 | 1860.5 | 57.41 |
| 430000 | 1851.4 | 58.26 |
| 440000 | 1842.5 | 59.11 |
| 450000 | 1833.7 | 59.96 |
| 460000 | 1825.0 | 60.82 |
| 470000 | 1816.5 | 61.69 |
| 480000 | 1808.0 | 62.55 |
| 490000 | 1799.7 | 63.42 |
| 500000 | 1791.5 | 64.30 |
| 510000 | 1783.4 | 65.18 |
| 520000 | 1775.5 | 66.06 |
| 530000 | 1767.6 | 66.95 |
| 540000 | 1759.8 | 67.84 |
| 550000 | 1752.1 | 68.73 |
| 560000 | 1744.6 | 69.63 |
| 570000 | 1737.1 | 70.53 |
| 580000 | 1729.7 | 71.44 |
| 590000 | 1722.4 | 72.35 |
| 600000 | 1715.3 | 73.26 |
| 610000 | 1708.2 | 74.18 |
| 620000 | 1701.1 | 75.10 |
| 630000 | 1694.2 | 76.03 |
| 640000 | 1687.4 | 76.96 |
| 650000 | 1680.6 | 77.89 |
| 660000 | 1673.9 | 78.83 |
| 670000 | 1667.3 | 79.77 |
| 680000 | 1660.8 | 80.71 |
| 690000 | 1654.3 | 81.66 |
| 700000 | 1648.0 | 82.61 |
| 710000 | 1641.7 | 83.56 |
| 720000 | 1635.4 | 84.52 |
| 730000 | 1629.3 | 85.48 |
| 740000 | 1623.2 | 86.45 |
| 750000 | 1617.2 | 87.42 |
| 760000 | 1611.2 | 88.39 |
| 770000 | 1605.3 | 89.37 |
| 780000 | 1599.5 | 90.35 |
| 790000 | 1593.7 | 91.33 |
| 800000 | 1588.0 | 92.32 |
| 810000 | 1582.4 | 93.31 |
| 820000 | 1576.8 | 94.31 |
| 830000 | 1571.3 | 95.30 |
| 840000 | 1565.8 | 96.31 |
| 850000 | 1560.4 | 97.31 |
| 860000 | 1555.0 | 98.32 |
| 870000 | 1549.7 | 99.33 |
| 880000 | 1544.5 | 100.35 |
| 885000 | 1541.9 | 100.86 |
| 890000 | 1539.3 | 101.37 |
| 900000 | 1534.2 | 102.39 |
| 910000 | 1529.1 | 103.41 |
| 920000 | 1524.0 | 104.44 |
| 930000 | 1519.1 | 105.47 |
| 940000 | 1514.1 | 106.51 |
| 950000 | 1509.2 | 107.55 |
| 960000 | 1504.4 | 108.59 |
| 970000 | 1499.6 | 109.64 |
| 980000 | 1494.8 | 110.69 |
| 990000 | 1490.1 | 111.74 |
| 1000000 | 1485.5 | 112.79 |
| 2 868 378 | 1008.910 | 6 hours |
| 8 140 000 | 635.4 | 24 hours |