Tutorial: Basic Orbiting (Technical)
Getting into space is relatively easy, but staying there without drifting endlessly into space or falling back down to Kearth can be challenging. This tutorial will teach you how to get into and remain in orbit, how to adjust your orbit to be circular or elliptical, and how to adjust to a higher or lower orbit.
Contents
[hide]Your first orbit
A good procedure for getting into orbit was posted by HarvesteR on the KSP forums (edited to take into account simulation changes since the original post): [Editor's Note: Use the Yellow Blip (Your TVV) to indicate your true direction of travel. Do not rely on your craft's orientation. You could be moving in a direction significantly different from where your craft is point its nose!]
- Launch straight up, and continue to climb up to about 15 000 m.
- Then, gradually start leveling off. You will start gaining horizontal speed.
[Editor's Note: Don't go much past 45 degrees until you are over 30 000 m this is because the atmosphere is still very thick until 30k! After 30k, crank over to horizontal steadily. You should be at about 70k-100k altitude now.]
- Now you're basically trading vertical speed for horizontal speed. The idea is to get to 0 vertical speed at about 75 000 m, and be moving horizontally at about 2 287 m/s.
[Editor's Note: If you have version 11 or better, try switching between the orbital map view and your ship view occasionally to see if you have a stable orbit established. You'll know it's stable when the indicator goes all the way around the planet.]
This will put you in a stable orbit. The altitude at which you start leveling off and the altitude at which you reach orbital velocity will depend a lot on how your rocket is designed. The idea, however, is to get out of the thickest part of the atmosphere before you start adding horizontal speed, so that you aren't wasting energy adding horizontal speed which will just bleed off due to air resistance.
It is likely that you will overshoot or undershoot these figures by a wide margin on your first couple attempts. Don't worry! Manual orbit insertion is difficult, that's why NASA uses computer guidance! When you finally do get into a stable orbit, you'll probably be on an elliptical trajectory; that is, your ship will coast away from the planet, gradually losing speed. When it reaches its maximum altitude, it will start to fall back toward Kearth, picking up speed again. If you're going fast enough, you'll fall "past" Kearth instead of into it, and that's orbiting.
Video Tutorial
Video Example Of Building A Rocket And Taking It To Orbit
Stabilizing your orbit
During each orbit, your craft will reach maximum altitude, called apoapsis, and on the opposite side of the planet, it will reach minimum altitude, called periapsis. At both apoapsis and periapsis, your vertical speed will be zero. These points are the easiest points to make orbital corrections, because you can easily determine how fast to go when your vertical speed is zero. Note: The relative difference between your orbit's apoapsis and periapsis is called its eccentricity. Orbits that are exactly circular have zero eccentricity, and highly "flattened-out" orbits have eccentricity close to 1.
There are a number of third-party calculators available which can crunch the numbers and tell you your eccentricity, as well as provide the speeds required to circularize your orbit at your current (or future) altitude. Whether you calculate your orbits by hand, or use a third party app, the general procedures are still the same and are given below:
First, in order to get into a nice, round orbit, you need to determine how fast to go. The higher your orbit, the less gravity you'll feel from Kearth, so the slower you'll need to go to be in a circular orbit. Consult the table below, or use a 3rd party table, to determine the proper speed for your altitude at apoapsis or periapsis. You'll probably want to watch your altimiter as you near one of the critical points, remember the altitude, look up the speed in the table, and make the correction on your next pass. If you want to "round out" your orbit from apoapsis, you need to speed up to avoid falling back down to periapsis. Point your craft in the exact direction of travel (use the green circular indicator on the gimbal to line up), and apply thrust until you've gained enough speed. To round out an orbit from periapsis, you need to slow down to avoid climbing back up to apoapsis. Point your craft in the opposite direction of travel (indicated on the gimbal by a green circle with an "X" through it), and apply thrust until you have slowed to the speed indicated by the table. You should then be in an orbit that is very close to circular! Depending on how eccentric your initial orbit was, you may need to make a large correction on your first pass followed by a small correction on a subsequent pass to get very stable.
If you have version 0.11 or better, adding a set of RCS thrusters to your craft can help make minute adjustments to an orbit easier. Version 0.11 also allows you to see the current trajectory (and read periapsis and apoapsis altitudes) by switching to the Map view (M key)
Transfer Orbits
The most efficient way to transfer from a lower circular orbit to a higher circular orbit (or vice-versa) is to use an elliptical transfer orbit, also known as a Hohmann transfer orbit. To transfer, we make the perikee of the elliptical orbit the same as the radius of the lower orbit, and the apokee of the elliptical orbit the same as the radius of the higher orbit. If you are going from low to high, you make a burn in the direction of travel to elongate your orbit. You will climb in altitude as you travel around the planet to the apokee of your transfer orbit. Then, make a second burn to round out the new, higher orbit (as described above). To go from high to low, do the opposite: Burn in the opposite direction of travel, then fall down to the perikee of your transfer orbit, and make a second burn to round out the lower orbit (again in the opposite direction of travel).
Target Speed
The key to transfer orbits is figuring out how much speed to add or subtract to reach a desired new orbital altitude. To do this, use the formula below to determine the target velocity for your initial burn:
v = 1 878 968 * sqrt(2/ri - 2/(rl + rh))
In this formula, rl and rh are the radii of the lower and higher orbits, respectively, and ri is the radius of the initial orbit. If you are transferring to a higher orbit, ri will be equal to rl, and v will be faster than your current speed, so burn in the direction of travel to reach v. If you are transferring to a lower orbit, ri will be equal to rh, and v will be slower than your current speed, so burn in the opposite direction to reach v. Remember, v is the target speed for your initial burn that puts you into the elliptical transfer orbit. Once you reach your new orbital altitude, you need to make a second burn to round out your orbit, using the same technique described in the stabilizing your orbit section.
Details of where this formula comes from are in the technical section below. When using this formula, take care to remember that the radius of an orbit is equal to the orbital altitude plus Kearth's radius (600 000 m).
De-orbiting
The most efficient way to de-orbit from any altitude is to initiate a transfer orbit with a perikee below 70000 m, the edge of Kearth's atmosphere. Note that the upper atmosphere is very thin so if you do not want to wait for several orbits of aerobraking, aim for under 35000 m and thicker air. As you approach perikee, the atmospheric drag will start to slow your craft and eventually it can no longer maintain orbit.
R code snippet for planning Hohmann transfer
hohmann <- function(from_alt,to_alt){
# provides information needed to perform
# a hohmann transfer from a circular ortbit
# at from_alt (km) to a circular orbit at to_alt (km)
mu <- 3530.394 # Gravitational parameter (km^3/s^2)
R <- 600 # Kearth radius (km)
r1 <- from_alt+R # radius 1 (km)
r2 <- to_alt+R # radius 2 (km)
vc1 <- sqrt(mu/r1) # circular orbit velocity 1 (km/s)
vc2 <- sqrt(mu/r2) # circular orbit velocity 2 (km/s)
a <- (r1+r2)/2 # semi-major axis of transfer orbit (km)
T <- 2*pi*sqrt((a^3)/mu) # period of transfer orbit (s)
dv1 <- (sqrt(r2/a)-1)*vc1 # delta v1 (km/s)
dv2 <- (1-sqrt(r1/a))*vc2 # delta v2 (km/s)
b1 <- list(from=vc1,to=vc1+dv1) # burn one from-to velocities (km/s)
t <- T/2 # time between burns (s)
b2 <- list(from=vc2+dv2,to=vc2) # burn two from-to velocities (km/s)
out <- list(from_alt=from_alt,b1=b1,t=t,b2=b2,to_alt=to_alt)
return(out)}
Example usage
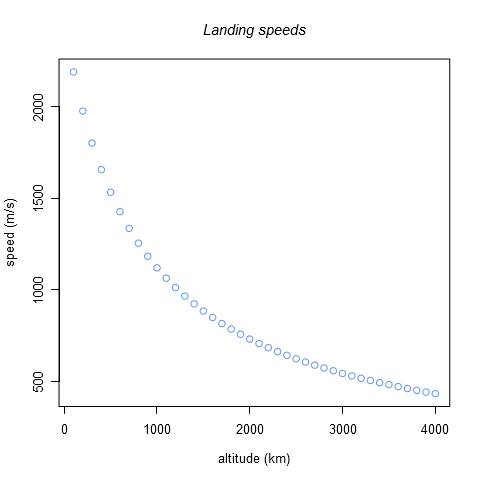
Produce a graph showing the speeds need to transfer from a range of circular orbit altitudes into a landing orbit.
plot(100*1:40,1000*hohmann(100*1:40,34)$b1$to,main="Landing speeds",xlab="altitude (km)",ylab="speed (m/s)")
R project Link[1]
Technical Details
Below are the formulae used to determine orbital speeds, and a table of orbital speeds up to 1000 km.
Orbital Speed
The relation between orbital speed and acceleration is given by the formula:
a = v2 / r,
where a is the acceleration due to gravity, v is the horizontal speed, and r is the radius of orbit.
Of course, gravity varies depending on your distance from the planet, so we also need the following formula to determine a based on your altitude:
a = g * (R / (R + h))2,
where g is the acceleration due to gravity at sea level (9.807 m/s2), R is the radius of Kearth (600 km), and h is the altitude of your orbit.
Note: From here, we will substitute R + h for r, since the radius of your orbit is equal to the radius of Kearth plus your altitude.
Substituting for a and simplifying, we get:
g * (R / (R + h))2 = v2 / (R + h)
g * R2 / (R + h) = v2
v = R * sqrt(g / (R + h))
Finally, substituting known values for g and R,
v = 600 000 m * sqrt(9.807 m/s2 / (600 000 m + h))
Orbital Period
When the orbital speed is known, the orbital period is simple to determine. From the basic mechanics formula:
d = v * t
We know v from the above, and d is simply the circumference of a circle with a radius equal to your orbital altitude plus the radius of Kearth:
t = 2π * (600 000 m + h) / v
Transfer Orbits
Coming soon!
Orbital Table
Note: The atmosphere previously had a sharp cutoff at 34.5 km, but now extends to approximately 68 km. Below this altitude, your orbit will gradually decay. The decay becomes quite rapid below about 45 km. The orbital parameters below 68 km are provided for reference, but understand that you will not be able to maintain these orbits without regular corrections to counteract the atmospheric drag.
| Altitude (m) | Horizontal Speed (m/s) | Orbital Period (min) |
|---|---|---|
| 35000 | 2357.9 | 28.20 |
| 36000 | 2356.1 | 28.27 |
| 37000 | 2354.2 | 28.33 |
| 38000 | 2352.4 | 28.40 |
| 39000 | 2350.5 | 28.47 |
| 40000 | 2348.7 | 28.54 |
| 41000 | 2346.9 | 28.60 |
| 42000 | 2345.0 | 28.67 |
| 43000 | 2343.2 | 28.74 |
| 44000 | 2341.4 | 28.80 |
| 45000 | 2339.6 | 28.87 |
| 46000 | 2337.8 | 28.94 |
| 47000 | 2336.0 | 29.00 |
| 48000 | 2334.2 | 29.07 |
| 49000 | 2332.4 | 29.14 |
| 50000 | 2330.6 | 29.21 |
| 51000 | 2328.8 | 29.27 |
| 52000 | 2327.0 | 29.34 |
| 53000 | 2325.2 | 29.41 |
| 54000 | 2323.4 | 29.48 |
| 55000 | 2321.7 | 29.54 |
| 56000 | 2319.9 | 29.61 |
| 57000 | 2318.1 | 29.68 |
| 58000 | 2316.4 | 29.75 |
| 59000 | 2314.6 | 29.82 |
| 60000 | 2312.8 | 29.88 |
| 61000 | 2311.1 | 29.95 |
| 62000 | 2309.4 | 30.02 |
| 63000 | 2307.6 | 30.09 |
| 64000 | 2305.9 | 30.16 |
| 65000 | 2304.1 | 30.22 |
| 66000 | 2302.4 | 30.29 |
| 67000 | 2300.7 | 30.36 |
| 68000 | 2299.0 | 30.43 |
| 69000 | 2297.2 | 30.50 |
| 70000 | 2295.5 | 30.56 |
| 71000 | 2293.8 | 30.63 |
| 72000 | 2292.1 | 30.70 |
| 73000 | 2290.4 | 30.77 |
| 74000 | 2288.7 | 30.84 |
| 75000 | 2287.0 | 30.91 |
| 76000 | 2285.3 | 30.98 |
| 77000 | 2283.6 | 31.05 |
| 78000 | 2281.9 | 31.11 |
| 79000 | 2280.3 | 31.18 |
| 80000 | 2278.6 | 31.25 |
| 81000 | 2276.9 | 31.32 |
| 82000 | 2275.2 | 31.39 |
| 83000 | 2273.6 | 31.46 |
| 84000 | 2271.9 | 31.53 |
| 85000 | 2270.3 | 31.60 |
| 86000 | 2268.6 | 31.67 |
| 87000 | 2266.9 | 31.74 |
| 88000 | 2265.3 | 31.80 |
| 89000 | 2263.7 | 31.87 |
| 90000 | 2262.0 | 31.94 |
| 91000 | 2260.4 | 32.01 |
| 92000 | 2258.7 | 32.08 |
| 93000 | 2257.1 | 32.15 |
| 94000 | 2255.5 | 32.22 |
| 95000 | 2253.9 | 32.29 |
| 96000 | 2252.2 | 32.36 |
| 97000 | 2250.6 | 32.43 |
| 98000 | 2249.0 | 32.50 |
| 99000 | 2247.4 | 32.57 |
| 100000 | 2245.8 | 32.64 |
| 105000 | 2237.8 | 32.99 |
| 110000 | 2229.9 | 33.34 |
| 115000 | 2222.1 | 33.70 |
| 120000 | 2214.4 | 34.05 |
| 125000 | 2206.7 | 34.40 |
| 130000 | 2199.2 | 34.76 |
| 135000 | 2191.7 | 35.12 |
| 140000 | 2184.3 | 35.48 |
| 145000 | 2176.9 | 35.84 |
| 150000 | 2169.6 | 36.20 |
| 155000 | 2162.4 | 36.56 |
| 160000 | 2155.3 | 36.93 |
| 165000 | 2148.3 | 37.29 |
| 170000 | 2141.3 | 37.66 |
| 175000 | 2134.4 | 38.02 |
| 180000 | 2127.5 | 38.39 |
| 185000 | 2120.7 | 38.76 |
| 190000 | 2114.0 | 39.13 |
| 195000 | 2107.3 | 39.51 |
| 200000 | 2100.7 | 39.88 |
| 205000 | 2094.2 | 40.25 |
| 210000 | 2087.7 | 40.63 |
| 215000 | 2081.3 | 41.01 |
| 220000 | 2075.0 | 41.38 |
| 225000 | 2068.7 | 41.76 |
| 230000 | 2062.4 | 42.14 |
| 235000 | 2056.3 | 42.52 |
| 240000 | 2050.1 | 42.91 |
| 245000 | 2044.0 | 43.29 |
| 250000 | 2038.0 | 43.68 |
| 255000 | 2032.1 | 44.06 |
| 260000 | 2026.1 | 44.45 |
| 265000 | 2020.3 | 44.84 |
| 270000 | 2014.5 | 45.23 |
| 275000 | 2008.7 | 45.62 |
| 280000 | 2003.0 | 46.01 |
| 285000 | 1997.3 | 46.40 |
| 290000 | 1991.7 | 46.79 |
| 295000 | 1986.1 | 47.19 |
| 300000 | 1980.6 | 47.59 |
| 305000 | 1975.1 | 47.98 |
| 310000 | 1969.7 | 48.38 |
| 315000 | 1964.3 | 48.78 |
| 320000 | 1959.0 | 49.18 |
| 325000 | 1953.7 | 49.58 |
| 330000 | 1948.4 | 49.98 |
| 335000 | 1943.2 | 50.39 |
| 340000 | 1938.0 | 50.79 |
| 345000 | 1932.9 | 51.20 |
| 350000 | 1927.8 | 51.61 |
| 355000 | 1922.7 | 52.01 |
| 360000 | 1917.7 | 52.42 |
| 365000 | 1912.7 | 52.83 |
| 370000 | 1907.8 | 53.24 |
| 375000 | 1902.9 | 53.66 |
| 380000 | 1898.0 | 54.07 |
| 385000 | 1893.2 | 54.48 |
| 390000 | 1888.4 | 54.90 |
| 395000 | 1883.7 | 55.32 |
| 400000 | 1879.0 | 55.73 |
| 405000 | 1874.3 | 56.15 |
| 410000 | 1869.6 | 56.57 |
| 415000 | 1865.0 | 56.99 |
| 420000 | 1860.5 | 57.41 |
| 425000 | 1855.9 | 57.84 |
| 430000 | 1851.4 | 58.26 |
| 435000 | 1846.9 | 58.68 |
| 440000 | 1842.5 | 59.11 |
| 445000 | 1838.1 | 59.54 |
| 450000 | 1833.7 | 59.96 |
| 455000 | 1829.3 | 60.39 |
| 460000 | 1825.0 | 60.82 |
| 465000 | 1820.7 | 61.25 |
| 470000 | 1816.5 | 61.69 |
| 475000 | 1812.2 | 62.12 |
| 480000 | 1808.0 | 62.55 |
| 485000 | 1803.9 | 62.99 |
| 490000 | 1799.7 | 63.42 |
| 495000 | 1795.6 | 63.86 |
| 500000 | 1791.5 | 64.30 |
| 505000 | 1787.5 | 64.74 |
| 510000 | 1783.4 | 65.18 |
| 515000 | 1779.4 | 65.62 |
| 520000 | 1775.5 | 66.06 |
| 525000 | 1771.5 | 66.50 |
| 530000 | 1767.6 | 66.95 |
| 535000 | 1763.7 | 67.39 |
| 540000 | 1759.8 | 67.84 |
| 545000 | 1756.0 | 68.28 |
| 550000 | 1752.1 | 68.73 |
| 555000 | 1748.3 | 69.18 |
| 560000 | 1744.6 | 69.63 |
| 565000 | 1740.8 | 70.08 |
| 570000 | 1737.1 | 70.53 |
| 575000 | 1733.4 | 70.98 |
| 580000 | 1729.7 | 71.44 |
| 585000 | 1726.1 | 71.89 |
| 590000 | 1722.4 | 72.35 |
| 595000 | 1718.8 | 72.80 |
| 600000 | 1715.3 | 73.26 |
| 605000 | 1711.7 | 73.72 |
| 610000 | 1708.2 | 74.18 |
| 615000 | 1704.6 | 74.64 |
| 620000 | 1701.1 | 75.10 |
| 625000 | 1697.7 | 75.56 |
| 630000 | 1694.2 | 76.03 |
| 635000 | 1690.8 | 76.49 |
| 640000 | 1687.4 | 76.96 |
| 645000 | 1684.0 | 77.42 |
| 650000 | 1680.6 | 77.89 |
| 655000 | 1677.2 | 78.36 |
| 660000 | 1673.9 | 78.83 |
| 665000 | 1670.6 | 79.29 |
| 670000 | 1667.3 | 79.77 |
| 675000 | 1664.0 | 80.24 |
| 680000 | 1660.8 | 80.71 |
| 685000 | 1657.6 | 81.18 |
| 690000 | 1654.3 | 81.66 |
| 695000 | 1651.1 | 82.13 |
| 700000 | 1648.0 | 82.61 |
| 705000 | 1644.8 | 83.09 |
| 710000 | 1641.7 | 83.56 |
| 715000 | 1638.5 | 84.04 |
| 720000 | 1635.4 | 84.52 |
| 725000 | 1632.3 | 85.00 |
| 730000 | 1629.3 | 85.48 |
| 735000 | 1626.2 | 85.97 |
| 740000 | 1623.2 | 86.45 |
| 745000 | 1620.2 | 86.93 |
| 750000 | 1617.2 | 87.42 |
| 755000 | 1614.2 | 87.91 |
| 760000 | 1611.2 | 88.39 |
| 765000 | 1608.2 | 88.88 |
| 770000 | 1605.3 | 89.37 |
| 775000 | 1602.4 | 89.86 |
| 780000 | 1599.5 | 90.35 |
| 785000 | 1596.6 | 90.84 |
| 790000 | 1593.7 | 91.33 |
| 795000 | 1590.9 | 91.83 |
| 800000 | 1588.0 | 92.32 |
| 805000 | 1585.2 | 92.82 |
| 810000 | 1582.4 | 93.31 |
| 815000 | 1579.6 | 93.81 |
| 820000 | 1576.8 | 94.31 |
| 825000 | 1574.0 | 94.81 |
| 830000 | 1571.3 | 95.30 |
| 835000 | 1568.5 | 95.80 |
| 840000 | 1565.8 | 96.31 |
| 845000 | 1563.1 | 96.81 |
| 850000 | 1560.4 | 97.31 |
| 855000 | 1557.7 | 97.81 |
| 860000 | 1555.0 | 98.32 |
| 865000 | 1552.4 | 98.82 |
| 870000 | 1549.7 | 99.33 |
| 875000 | 1547.1 | 99.84 |
| 880000 | 1544.5 | 100.35 |
| 885000 | 1541.9 | 100.86 |
| 890000 | 1539.3 | 101.37 |
| 895000 | 1536.7 | 101.88 |
| 900000 | 1534.2 | 102.39 |
| 905000 | 1531.6 | 102.90 |
| 910000 | 1529.1 | 103.41 |
| 915000 | 1526.6 | 103.93 |
| 920000 | 1524.0 | 104.44 |
| 925000 | 1521.5 | 104.96 |
| 930000 | 1519.1 | 105.47 |
| 935000 | 1516.6 | 105.99 |
| 940000 | 1514.1 | 106.51 |
| 945000 | 1511.7 | 107.03 |
| 950000 | 1509.2 | 107.55 |
| 955000 | 1506.8 | 108.07 |
| 960000 | 1504.4 | 108.59 |
| 965000 | 1502.0 | 109.11 |
| 970000 | 1499.6 | 109.64 |
| 975000 | 1497.2 | 110.16 |
| 980000 | 1494.8 | 110.69 |
| 985000 | 1492.5 | 111.21 |
| 990000 | 1490.1 | 111.74 |
| 995000 | 1487.8 | 112.27 |
| 1000000 | 1485.5 | 112.79 |
| 8 140 000 | 635.4 | 24 hours |