Tutorial: Basic Orbiting (Technical)
Getting into space is relatively easy, but staying there without drifting endlessly into space or falling back down to Kearth can be challenging. This tutorial will teach you how to get into and remain in orbit, how to adjust your orbit to be circular or elliptical, and how to adjust to a higher or lower orbit.
Contents
Your first orbit
A good procedure for getting into orbit was posted by HarvesteR on the KSP forums (edited to take into account simulation changes since the original post):
- Launch straight up, and continue to climb up to about 15 000 m.
- Then, gradually start leveling off. You will start gaining horizontal speed.
- Now you're basically trading vertical speed for horizontal speed. The idea is to get to 0 vertical speed at about 75 000 m, and be moving horizontally at about 2 287 m/s.
This will put you in a stable orbit. The altitude at which you start leveling off and the altitude at which you reach orbital velocity will depend a lot on how your rocket is designed. The idea, however, is to get out of the thickest part of the atmosphere before you start adding horizontal speed, so that you aren't wasting energy adding horizontal speed which will just bleed off due to air resistance.
It is likely that you will overshoot or undershoot these figures by a wide margin on your first couple attempts. Don't worry! Manual orbit insertion is difficult, that's why NASA uses computer guidance! When you finally do get into a stable orbit, you'll probably be on an elliptical trajectory; that is, your ship will coast away from the planet, gradually losing speed. When it reaches its maximum altitude, it will start to fall back toward Kearth, picking up speed again. If you're going fast enough, you'll fall "past" Kearth instead of into it, and that's orbiting.
Video Tutorial
Video Example Of Building A Rocket And Taking It To Orbit
No more s***. All posts of this qluatiy from now on
Transfer Orbits
The most efficient way to transfer from a lower circular orbit to a higher circular orbit (or vice-versa) is to use an elliptical transfer orbit, also known as a Hohmann transfer orbit. To transfer, we make the perikee of the elliptical orbit the same as the radius of the lower orbit, and the apokee of the elliptical orbit the same as the radius of the higher orbit. If you are going from low to high, you make a burn in the direction of travel to elongate your orbit. You will climb in altitude as you travel around the planet to the apokee of your transfer orbit. Then, make a second burn to round out the new, higher orbit (as described above). To go from high to low, do the opposite: Burn in the opposite direction of travel, then fall down to the perikee of your transfer orbit, and make a second burn to round out the lower orbit (again in the opposite direction of travel).
Target Speed
The key to transfer orbits is figuring out how much speed to add or subtract to reach a desired new orbital altitude. To do this, use the formula below to determine the target velocity for your initial burn:
v = 1 878 968 * sqrt(2/ri - 2/(rl + rh))
In this formula, rl and rh are the radii of the lower and higher orbits, respectively, and ri is the radius of the initial orbit. If you are transferring to a higher orbit, ri will be equal to rl, and v will be faster than your current speed, so burn in the direction of travel to reach v. If you are transferring to a lower orbit, ri will be equal to rh, and v will be slower than your current speed, so burn in the opposite direction to reach v. Remember, v is the target speed for your initial burn that puts you into the elliptical transfer orbit. Once you reach your new orbital altitude, you need to make a second burn to round out your orbit, using the same technique described in the stabilizing your orbit section.
Details of where this formula comes from are in the technical section below. When using this formula, take care to remember that the radius of an orbit is equal to the orbital altitude plus Kearth's radius (600 000 m).
De-orbiting
The most efficient way to de-orbit from any altitude is to initiate a transfer orbit with a perikee below 70000 m, the edge of Kearth's atmosphere. Note that the upper atmosphere is very thin so if you do not want to wait for several orbits of aerobraking, aim for under 35000 m and thicker air. As you approach perikee, the atmospheric drag will start to slow your craft and eventually it can no longer maintain orbit.
R code snippet for planning Hohmann transfer
hohmann <- function(from_alt,to_alt){
# provides information needed to perform
# a hohmann transfer from a circular ortbit
# at from_alt (km) to a circular orbit at to_alt (km)
mu <- 3530.394 # Gravitational parameter (km^3/s^2)
R <- 600 # Kearth radius (km)
r1 <- from_alt+R # radius 1 (km)
r2 <- to_alt+R # radius 2 (km)
vc1 <- sqrt(mu/r1) # circular orbit velocity 1 (km/s)
vc2 <- sqrt(mu/r2) # circular orbit velocity 2 (km/s)
a <- (r1+r2)/2 # semi-major axis of transfer orbit (km)
T <- 2*pi*sqrt((a^3)/mu) # period of transfer orbit (s)
dv1 <- (sqrt(r2/a)-1)*vc1 # delta v1 (km/s)
dv2 <- (1-sqrt(r1/a))*vc2 # delta v2 (km/s)
b1 <- list(from=vc1,to=vc1+dv1) # burn one from-to velocities (km/s)
t <- T/2 # time between burns (s)
b2 <- list(from=vc2+dv2,to=vc2) # burn two from-to velocities (km/s)
out <- list(from_alt=from_alt,b1=b1,t=t,b2=b2,to_alt=to_alt)
return(out)}
Example usage
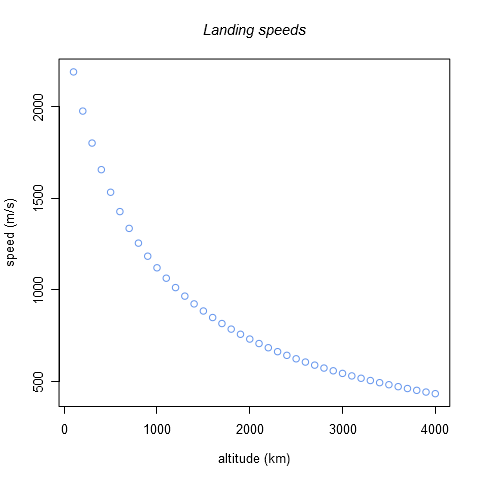
Produce a graph showing the speeds need to transfer from a range of circular orbit altitudes into a landing orbit.
plot(100*1:40,1000*hohmann(100*1:40,34)$b1$to,main="Landing speeds",xlab="altitude (km)",ylab="speed (m/s)")
R project Link[1]
Technical Details
Below are the formulae used to determine orbital speeds, and a table of orbital speeds up to 1000 km.
Orbital Speed
The relation between orbital speed and acceleration is given by the formula:
a = v2 / r,
where a is the acceleration due to gravity, v is the horizontal speed, and r is the radius of orbit.
Of course, gravity varies depending on your distance from the planet, so we also need the following formula to determine a based on your altitude:
a = g * (R / (R + h))2,
where g is the acceleration due to gravity at sea level (9.807 m/s2), R is the radius of Kearth (600 km), and h is the altitude of your orbit.
Note: From here, we will substitute R + h for r, since the radius of your orbit is equal to the radius of Kearth plus your altitude.
Substituting for a and simplifying, we get:
g * (R / (R + h))2 = v2 / (R + h)
g * R2 / (R + h) = v2
v = R * sqrt(g / (R + h))
Finally, substituting known values for g and R,
v = 600 000 m * sqrt(9.807 m/s2 / (600 000 m + h))
Orbital Period
When the orbital speed is known, the orbital period is simple to determine. From the basic mechanics formula:
d = v * t
We know v from the above, and d is simply the circumference of a circle with a radius equal to your orbital altitude plus the radius of Kearth:
t = 2π * (600 000 m + h) / v
Transfer Orbits
Coming soon!
Orbital Table
Note: The atmosphere previously had a sharp cutoff at 34.5 km, but now extends to approximately 68 km. Below this altitude, your orbit will gradually decay. The decay becomes quite rapid below about 45 km. The orbital parameters below 68 km are provided for reference, but understand that you will not be able to maintain these orbits without regular corrections to counteract the atmospheric drag.
| Altitude (m) | Horizontal Speed (m/s) | Orbital Period (min) |
|---|---|---|
| 35000 | 2357.9 | 28.20 |
| 36000 | 2356.1 | 28.27 |
| 37000 | 2354.2 | 28.33 |
| 38000 | 2352.4 | 28.40 |
| 39000 | 2350.5 | 28.47 |
| 40000 | 2348.7 | 28.54 |
| 41000 | 2346.9 | 28.60 |
| 42000 | 2345.0 | 28.67 |
| 43000 | 2343.2 | 28.74 |
| 44000 | 2341.4 | 28.80 |
| 45000 | 2339.6 | 28.87 |
| 46000 | 2337.8 | 28.94 |
| 47000 | 2336.0 | 29.00 |
| 48000 | 2334.2 | 29.07 |
| 49000 | 2332.4 | 29.14 |
| 50000 | 2330.6 | 29.21 |
| 51000 | 2328.8 | 29.27 |
| 52000 | 2327.0 | 29.34 |
| 53000 | 2325.2 | 29.41 |
| 54000 | 2323.4 | 29.48 |
| 55000 | 2321.7 | 29.54 |
| 56000 | 2319.9 | 29.61 |
| 57000 | 2318.1 | 29.68 |
| 58000 | 2316.4 | 29.75 |
| 59000 | 2314.6 | 29.82 |
| 60000 | 2312.8 | 29.88 |
| 61000 | 2311.1 | 29.95 |
| 62000 | 2309.4 | 30.02 |
| 63000 | 2307.6 | 30.09 |
| 64000 | 2305.9 | 30.16 |
| 65000 | 2304.1 | 30.22 |
| 66000 | 2302.4 | 30.29 |
| 67000 | 2300.7 | 30.36 |
| 68000 | 2299.0 | 30.43 |
| 69000 | 2297.2 | 30.50 |
| 70000 | 2295.5 | 30.56 |
| 71000 | 2293.8 | 30.63 |
| 72000 | 2292.1 | 30.70 |
| 73000 | 2290.4 | 30.77 |
| 74000 | 2288.7 | 30.84 |
| 75000 | 2287.0 | 30.91 |
| 76000 | 2285.3 | 30.98 |
| 77000 | 2283.6 | 31.05 |
| 78000 | 2281.9 | 31.11 |
| 79000 | 2280.3 | 31.18 |
| 80000 | 2278.6 | 31.25 |
| 81000 | 2276.9 | 31.32 |
| 82000 | 2275.2 | 31.39 |
| 83000 | 2273.6 | 31.46 |
| 84000 | 2271.9 | 31.53 |
| 85000 | 2270.3 | 31.60 |
| 86000 | 2268.6 | 31.67 |
| 87000 | 2266.9 | 31.74 |
| 88000 | 2265.3 | 31.80 |
| 89000 | 2263.7 | 31.87 |
| 90000 | 2262.0 | 31.94 |
| 91000 | 2260.4 | 32.01 |
| 92000 | 2258.7 | 32.08 |
| 93000 | 2257.1 | 32.15 |
| 94000 | 2255.5 | 32.22 |
| 95000 | 2253.9 | 32.29 |
| 96000 | 2252.2 | 32.36 |
| 97000 | 2250.6 | 32.43 |
| 98000 | 2249.0 | 32.50 |
| 99000 | 2247.4 | 32.57 |
| 100000 | 2245.8 | 32.64 |
| 105000 | 2237.8 | 32.99 |
| 110000 | 2229.9 | 33.34 |
| 115000 | 2222.1 | 33.70 |
| 120000 | 2214.4 | 34.05 |
| 125000 | 2206.7 | 34.40 |
| 130000 | 2199.2 | 34.76 |
| 135000 | 2191.7 | 35.12 |
| 140000 | 2184.3 | 35.48 |
| 145000 | 2176.9 | 35.84 |
| 150000 | 2169.6 | 36.20 |
| 155000 | 2162.4 | 36.56 |
| 160000 | 2155.3 | 36.93 |
| 165000 | 2148.3 | 37.29 |
| 170000 | 2141.3 | 37.66 |
| 175000 | 2134.4 | 38.02 |
| 180000 | 2127.5 | 38.39 |
| 185000 | 2120.7 | 38.76 |
| 190000 | 2114.0 | 39.13 |
| 195000 | 2107.3 | 39.51 |
| 200000 | 2100.7 | 39.88 |
| 205000 | 2094.2 | 40.25 |
| 210000 | 2087.7 | 40.63 |
| 215000 | 2081.3 | 41.01 |
| 220000 | 2075.0 | 41.38 |
| 225000 | 2068.7 | 41.76 |
| 230000 | 2062.4 | 42.14 |
| 235000 | 2056.3 | 42.52 |
| 240000 | 2050.1 | 42.91 |
| 245000 | 2044.0 | 43.29 |
| 250000 | 2038.0 | 43.68 |
| 255000 | 2032.1 | 44.06 |
| 260000 | 2026.1 | 44.45 |
| 265000 | 2020.3 | 44.84 |
| 270000 | 2014.5 | 45.23 |
| 275000 | 2008.7 | 45.62 |
| 280000 | 2003.0 | 46.01 |
| 285000 | 1997.3 | 46.40 |
| 290000 | 1991.7 | 46.79 |
| 295000 | 1986.1 | 47.19 |
| 300000 | 1980.6 | 47.59 |
| 305000 | 1975.1 | 47.98 |
| 310000 | 1969.7 | 48.38 |
| 315000 | 1964.3 | 48.78 |
| 320000 | 1959.0 | 49.18 |
| 325000 | 1953.7 | 49.58 |
| 330000 | 1948.4 | 49.98 |
| 335000 | 1943.2 | 50.39 |
| 340000 | 1938.0 | 50.79 |
| 345000 | 1932.9 | 51.20 |
| 350000 | 1927.8 | 51.61 |
| 355000 | 1922.7 | 52.01 |
| 360000 | 1917.7 | 52.42 |
| 365000 | 1912.7 | 52.83 |
| 370000 | 1907.8 | 53.24 |
| 375000 | 1902.9 | 53.66 |
| 380000 | 1898.0 | 54.07 |
| 385000 | 1893.2 | 54.48 |
| 390000 | 1888.4 | 54.90 |
| 395000 | 1883.7 | 55.32 |
| 400000 | 1879.0 | 55.73 |
| 405000 | 1874.3 | 56.15 |
| 410000 | 1869.6 | 56.57 |
| 415000 | 1865.0 | 56.99 |
| 420000 | 1860.5 | 57.41 |
| 425000 | 1855.9 | 57.84 |
| 430000 | 1851.4 | 58.26 |
| 435000 | 1846.9 | 58.68 |
| 440000 | 1842.5 | 59.11 |
| 445000 | 1838.1 | 59.54 |
| 450000 | 1833.7 | 59.96 |
| 455000 | 1829.3 | 60.39 |
| 460000 | 1825.0 | 60.82 |
| 465000 | 1820.7 | 61.25 |
| 470000 | 1816.5 | 61.69 |
| 475000 | 1812.2 | 62.12 |
| 480000 | 1808.0 | 62.55 |
| 485000 | 1803.9 | 62.99 |
| 490000 | 1799.7 | 63.42 |
| 495000 | 1795.6 | 63.86 |
| 500000 | 1791.5 | 64.30 |
| 505000 | 1787.5 | 64.74 |
| 510000 | 1783.4 | 65.18 |
| 515000 | 1779.4 | 65.62 |
| 520000 | 1775.5 | 66.06 |
| 525000 | 1771.5 | 66.50 |
| 530000 | 1767.6 | 66.95 |
| 535000 | 1763.7 | 67.39 |
| 540000 | 1759.8 | 67.84 |
| 545000 | 1756.0 | 68.28 |
| 550000 | 1752.1 | 68.73 |
| 555000 | 1748.3 | 69.18 |
| 560000 | 1744.6 | 69.63 |
| 565000 | 1740.8 | 70.08 |
| 570000 | 1737.1 | 70.53 |
| 575000 | 1733.4 | 70.98 |
| 580000 | 1729.7 | 71.44 |
| 585000 | 1726.1 | 71.89 |
| 590000 | 1722.4 | 72.35 |
| 595000 | 1718.8 | 72.80 |
| 600000 | 1715.3 | 73.26 |
| 605000 | 1711.7 | 73.72 |
| 610000 | 1708.2 | 74.18 |
| 615000 | 1704.6 | 74.64 |
| 620000 | 1701.1 | 75.10 |
| 625000 | 1697.7 | 75.56 |
| 630000 | 1694.2 | 76.03 |
| 635000 | 1690.8 | 76.49 |
| 640000 | 1687.4 | 76.96 |
| 645000 | 1684.0 | 77.42 |
| 650000 | 1680.6 | 77.89 |
| 655000 | 1677.2 | 78.36 |
| 660000 | 1673.9 | 78.83 |
| 665000 | 1670.6 | 79.29 |
| 670000 | 1667.3 | 79.77 |
| 675000 | 1664.0 | 80.24 |
| 680000 | 1660.8 | 80.71 |
| 685000 | 1657.6 | 81.18 |
| 690000 | 1654.3 | 81.66 |
| 695000 | 1651.1 | 82.13 |
| 700000 | 1648.0 | 82.61 |
| 705000 | 1644.8 | 83.09 |
| 710000 | 1641.7 | 83.56 |
| 715000 | 1638.5 | 84.04 |
| 720000 | 1635.4 | 84.52 |
| 725000 | 1632.3 | 85.00 |
| 730000 | 1629.3 | 85.48 |
| 735000 | 1626.2 | 85.97 |
| 740000 | 1623.2 | 86.45 |
| 745000 | 1620.2 | 86.93 |
| 750000 | 1617.2 | 87.42 |
| 755000 | 1614.2 | 87.91 |
| 760000 | 1611.2 | 88.39 |
| 765000 | 1608.2 | 88.88 |
| 770000 | 1605.3 | 89.37 |
| 775000 | 1602.4 | 89.86 |
| 780000 | 1599.5 | 90.35 |
| 785000 | 1596.6 | 90.84 |
| 790000 | 1593.7 | 91.33 |
| 795000 | 1590.9 | 91.83 |
| 800000 | 1588.0 | 92.32 |
| 805000 | 1585.2 | 92.82 |
| 810000 | 1582.4 | 93.31 |
| 815000 | 1579.6 | 93.81 |
| 820000 | 1576.8 | 94.31 |
| 825000 | 1574.0 | 94.81 |
| 830000 | 1571.3 | 95.30 |
| 835000 | 1568.5 | 95.80 |
| 840000 | 1565.8 | 96.31 |
| 845000 | 1563.1 | 96.81 |
| 850000 | 1560.4 | 97.31 |
| 855000 | 1557.7 | 97.81 |
| 860000 | 1555.0 | 98.32 |
| 865000 | 1552.4 | 98.82 |
| 870000 | 1549.7 | 99.33 |
| 875000 | 1547.1 | 99.84 |
| 880000 | 1544.5 | 100.35 |
| 885000 | 1541.9 | 100.86 |
| 890000 | 1539.3 | 101.37 |
| 895000 | 1536.7 | 101.88 |
| 900000 | 1534.2 | 102.39 |
| 905000 | 1531.6 | 102.90 |
| 910000 | 1529.1 | 103.41 |
| 915000 | 1526.6 | 103.93 |
| 920000 | 1524.0 | 104.44 |
| 925000 | 1521.5 | 104.96 |
| 930000 | 1519.1 | 105.47 |
| 935000 | 1516.6 | 105.99 |
| 940000 | 1514.1 | 106.51 |
| 945000 | 1511.7 | 107.03 |
| 950000 | 1509.2 | 107.55 |
| 955000 | 1506.8 | 108.07 |
| 960000 | 1504.4 | 108.59 |
| 965000 | 1502.0 | 109.11 |
| 970000 | 1499.6 | 109.64 |
| 975000 | 1497.2 | 110.16 |
| 980000 | 1494.8 | 110.69 |
| 985000 | 1492.5 | 111.21 |
| 990000 | 1490.1 | 111.74 |
| 995000 | 1487.8 | 112.27 |
| 1000000 | 1485.5 | 112.79 |
| 8 140 000 | 635.4 | 24 hours |