Difference between revisions of "Terminology/zh-cn"
From Kerbal Space Program Wiki
(Structure Update, to be in line with English page) |
|||
| Line 6: | Line 6: | ||
<div style="float:right;">[[File:cartesian.svg|thumb|upright|left|笛卡尔坐标系——使用直角坐标]][[File:polar.svg|thumb|upright|极坐标系——使用角度和长度]]</div> | <div style="float:right;">[[File:cartesian.svg|thumb|upright|left|笛卡尔坐标系——使用直角坐标]][[File:polar.svg|thumb|upright|极坐标系——使用角度和长度]]</div> | ||
| − | ; | + | ;椭圆(Elliptical) |
| − | : | + | :椭圆形,环绕轨道的常见状态。 |
| + | ;双曲线(Hyperbolic) | ||
| + | :开放的光滑曲线,通常对应的是逃逸轨道。 | ||
;法向量(normal vector) | ;法向量(normal vector) | ||
:一条与平面垂直的向量。 | :一条与平面垂直的向量。 | ||
;标量(scalar) | ;标量(scalar) | ||
| − | :一个没有方向的数值。标量一般会有测量单位的后缀,表明这个标量的量纲。 比如 3 米每秒(m/s), 3 米(m),3 秒(s) | + | :一个没有方向的数值。标量一般会有测量单位的后缀,表明这个标量的量纲。 比如 3 米每秒(m/s), 3 米(m),3 秒(s) 都是标量:它们分别是速率(区分于速度)、路程(区分于位移)和时间的单位,但不含方向。 |
;向量, 矢量(vector) | ;向量, 矢量(vector) | ||
| − | :一个方向和大小的集合。比如前进方向和速率放在一起就是速度。一个向量如何被表示取决于采用的坐标系,以及多少个维度被使用。 <35°, 12>是一个二维的极坐标向量,而<14, 9, -20> | + | :一个方向和大小的集合。比如前进方向和速率放在一起就是速度。一个向量如何被表示取决于采用的坐标系,以及多少个维度被使用。 <35°, 12>是一个二维的极坐标向量,而<14, 9, -20>则是一个三维笛卡尔(直角)坐标向量。也有其他的坐标系,但这些是最常用的。 |
:<35°, 12>是一个12个单位长的箭头,从原点(零点,角度在这里没有意义,因为这是一个没有长度的点)出发,结束在一个与偏离极轴(通常是x轴,逆时针旋转为正角度)35°的点。 | :<35°, 12>是一个12个单位长的箭头,从原点(零点,角度在这里没有意义,因为这是一个没有长度的点)出发,结束在一个与偏离极轴(通常是x轴,逆时针旋转为正角度)35°的点。 | ||
Revision as of 03:28, 12 May 2015
KSP中使用了大量物理学和轨道飞行的术语,面对这些词语时,非专业人员无疑是会异常困惑,更不要说还有大量的其他科学词汇和缩写了。
本页就是一个相关术语简洁的查询表单,希望能帮助你顺利的走上专业宇航员之路。
数学
- 椭圆(Elliptical)
- 椭圆形,环绕轨道的常见状态。
- 双曲线(Hyperbolic)
- 开放的光滑曲线,通常对应的是逃逸轨道。
- 法向量(normal vector)
- 一条与平面垂直的向量。
- 标量(scalar)
- 一个没有方向的数值。标量一般会有测量单位的后缀,表明这个标量的量纲。 比如 3 米每秒(m/s), 3 米(m),3 秒(s) 都是标量:它们分别是速率(区分于速度)、路程(区分于位移)和时间的单位,但不含方向。
- 向量, 矢量(vector)
- 一个方向和大小的集合。比如前进方向和速率放在一起就是速度。一个向量如何被表示取决于采用的坐标系,以及多少个维度被使用。 <35°, 12>是一个二维的极坐标向量,而<14, 9, -20>则是一个三维笛卡尔(直角)坐标向量。也有其他的坐标系,但这些是最常用的。
- <35°, 12>是一个12个单位长的箭头,从原点(零点,角度在这里没有意义,因为这是一个没有长度的点)出发,结束在一个与偏离极轴(通常是x轴,逆时针旋转为正角度)35°的点。
- <14, 9, -20>是一个从原点(<0,0,0>)出发,在一个x坐标为14,y坐标为9,z坐标为20的点终止的箭头。
- 使用直角坐标系的优点是你可以准确地知道向量的终止位置在哪里,但是计算向量的长度则比较麻烦。而在极坐标系中,向量长度十分易得,终止位置却较难得出。
- 速度、加速度、力、动量等物理量都是矢量。
一个三维坐标系需要:
- 一个原点。
- 3个单位向量。这些向量定义了沿着坐标轴的基本量度和坐标轴的方向。
- 3个标量,这可以是角度或坐标,用来描述坐标空间中的位置。
轨道
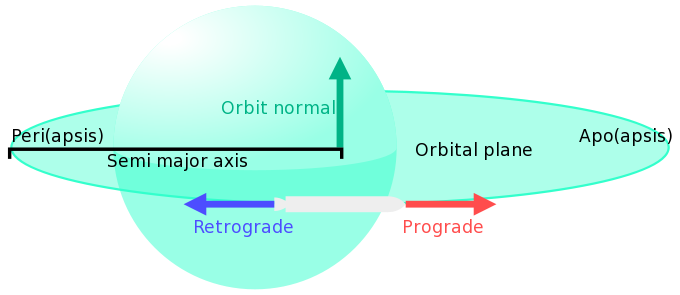
- 轨道远点(apoapsis)
- 椭圆轨道上,距离轨道中心天体最远的点。
- 轨道近点(periapsis)
- 椭圆轨道上,距离轨道中心天体最近的点。
- 近-* 和 远-* (peri-* and apo-*)
- 谈到轨道,我们通常都用具体的天体名称来指明轨道中心。因此,在这个游戏中,对于环绕Kerbin的轨道,我们会用近Kerbin点(Perikee, Perikerb)、远Kerbin点(Apokee, Apokerb)这样的名称。
- 升交点(ascending node)
- 以中心天体为参考系,轨道开始向“北”运动的点。“北”向,是参考轨道中心天体的坐标系。
- 降交点(descending node)
- 以中心天体为参考系,轨道开始向南运动的点。
- 离心率(eccentricity)
- 描述轨道几何特征的参数。
- ecc = 0 → 圆形轨道;
- 0 < ecc < 1 → 椭圆轨道;
- ecc = 1 → 抛物线轨道 - 这是一种逃逸轨道;
- ecc > 1 → 双曲线轨道 - 这是另一种逃逸轨道;
- 轨道倾角(inclination)
- 轨道平面与参考平面的夹角。(例如,90° 赤道平面倾角轨道就是所谓的极地轨道。)
- 近Kerbin轨道(low Kerbin orbit, LKO)
- 大多数天体的低轨道都存在于其重力范围内。该轨道高度低,但是稳定(高于大气层)。低轨道通常都是后续飞行的基础,位于上升段和向其他最终的目的地出发之间,在轨道的任意点都可以进行飞船脱离轨道的点火推进。其优点就是抵达低轨道所需要的燃料是最少的。
- 天顶(zenith)
- 地面座标系统中“正上方”的点,也就是火箭在发射场等待发射时指向的点,亦即,“天空中最高的点”。
- 天底(nadir)
- “天顶”的反向点。
- 轨道点(orbital nodes)
- 轨道中的特定点,如近点、远点,以及与其他轨道的交汇点等等。
- 轨道法向(orbit normal)
- 轨道平面的正交方向矢量。飞船速度矢量方向与重力矢量方向的矢量和就是轨道法向。其遵照右手规则,飞船在轨道逆时针飞行时,其轨道法向朝“上”,顺时针则朝下。而“上”也就是“北”,或“N+”,“下”也叫做“逆法向”,“南”或者 “N-”。
- 轨道平面(orbital plane)
- 描述轨道环绕飞行平面的虚拟圆盘(通常用于表述轨道倾角)。
- 顺行(prograde)
- 轨道路径的前进方向。由于轨道为椭圆形,因此实际上它的方向是飞船所处轨道位置的切线方向。
- 逆行(retrograde)
- 顺行的反向。
- 参考平面(reference plane)
- 所有飞行器在描述其所处轨道时都需要一个参考平面。对于行星轨道,通常是采用其赤道平面作为参照。类似太阳系的多天体平面为参考时,以黄道平面作为参考平面。在以其他轨道为目标飞行时,应采用目标轨道平面。轨道偏心率和上升点经度(以参考平面为坐标系)即可确定轨道平面。
- 半长轴(semi-major axis)
- 长轴是过焦点与椭圆相交的线长,而半长轴就是椭圆长轴的一半。在 KSP 中,半长轴的计算公式是:
。 轨道运行体的半长轴就是其中心椭圆轨道近点、远点距离的平均值。由于轨道远近点都是相对于轨道中心物体表面的距离,因此需要在公式中加入其半径。半长轴相同的轨道运行周期相同,无论离心率如何。
- 亚轨道(sub-orbit)
- 亚轨道近点位于行星表面之下,亚轨道飞行最终会与该行星发生交会碰撞。
- 推重比(thrust-weight-ratio, TWR)
- 飞船总质量与动力段所有发动机总推力的比值。若TWR>1,飞船可以完成加速和上升。若TWR<1,飞船是无法克服重力和低飞行高度空气阻力的,不过低 TWR 在太空或许可以足够保证飞行器的运动。因为飞船重量(W)与其所处位置的重力加速度(g)成正比,TWR也跟具体位置有关。Mün表面的重力加速度只是Kerbin表面重力加速度的16.6%,因此,TWRKerbin = 1相当于TWRMün = 6。
Ship Orientation
The ship orientation is always relative to a specific object. The terms are usually defined relative to the cockpit.
- Zenith
- Top side of the ship which is usually oriented away from the orbited body. Opposite of nadir.
- Nadir
- Bottom side of the ship which usually oriented towards the orbited body. Opposite of zenith.
- Port(side)
- Left side of the ship. Opposite of starboard.
- Starboard
- Right side of the ship. Opposite of portside.
- Front
- Front side/end of the ship which is usually towards the nose or prograde vector. Opposite of aft.
- Aft
- Back side/end of the ship which is usually housing the primary rockets and facing in retrograde. Opposite of front.
太空机动
- 大气层制动(atmospheric braking)
- → 全文: 空气制动
- 降低轨道近点,使其进入行星的大气层。这种飞行方式可以利用空气阻力降低飞行器的速度。它可以用于再进入(参考下文),也可以应用于轨道的调整,同时节约燃料。
- 点火(burn)
- 点燃发动机,通常目的是进行轨道调整。
- 圆化调整(circularizing)
- 这种机动(发动机点火推进)的目的是把轨道的偏心率调整到近似于零。通常是在轨道近/远点打开发动机推力来实现。
- 再入(re-entry)
- 就是再进入大气层,并利用空气阻力减速,使飞船进入地面返回轨道。由于需要足够高的速度来避免大气层把飞船“反弹”回太空,这种机动通常都会面临着剧烈的升温压力。在目前的游戏版本中,再进入过程只是个半成品,升温和大气反弹都没有实现。(不过有相关的MOD实现这个特性)
- 反向点火(retroburn)
- 向飞船前进的反方向点火推进,例如,把发动机喷口转向顺行方向,飞船头部对准逆行方向。这是一个常用的机动,可以在不改变其他轨道参数的情况下降低轨道速度。
物理
- 加速度(acceleration)
- 速度的改变率。加速度是矢量,单位为“米/秒2”(m/s2).
- 抛物线轨道(ballistic trajectory)
- 下落物体的轨道就是抛物线。在火箭飞行中,它就是指飞行器只受重力影响,本身没有任何动力(如推力)的飞行轨道。
- 速度改变量(Δv, delta-v)
- 飞行器速度的实际改变量或可能改变量。测量单位为米每秒(m/s)。质量增大在单位时间内会降低Δv,而增加推力可以在单位时间内提高Δv。这是一个有效计算推进效率的参量。例如,飞行器脱离Kerbin大气层并进入稳定轨道所需要的Δv大约是4,000 m/s。
- 能量(energy)
- 在轨飞行器的能量是其动能和势能之和。势能的计算公式是 ,动能的计算公式是 ,这里G是万有引力常量,M是行星的质量,m是飞行器的质量,R是距行星中心的距离,而v就是飞行器的速度。,总能量大于零,飞行器就进入逃逸轨道。相同半长轴的轨道能量相等。
- 逃逸速度(escape velocity)
- 脱离行星引力范围所需要的速度,其计算公式为 ,G是万有引力常量,M是行星的质量,r是行星半径。
- g力(G-force)
- g力是一个加速度的量度,不过其考虑了重力的影响。地球海平面测量得到的重力加速度约为9.81 m/s²,将此定义为1G。地球表面物体的加速度大约都是1G。某物体如果其加速度为2G,其重力则增加一倍。在轨运行并关闭发动机的航天器处于自由落体状态,此时为0G。
- 引力(gravity)
- 以物体的引力质量为力荷的力。本身非常微弱,只是那些质量很高的物体才能产生明显的引力,如行星、月亮等。其大小与物体中心距离的平方呈反比。所以距离增加 1 倍,其引力会降低到1/22=1/4。
- 引力井(gravity wall)
- 行星引力的作用范围。实际上这个区域是无限延伸的,但是由于引力会随着距离的增大急剧降低,其范围只是引力明显起作用的区域。
- 轨道(orbit)
- 当某物体具有足够大的切线速度(而且其位于大气层之外,无明显的空气阻力减速时),它会绕行星运行,并且不会落向该行星,这个运动轨迹就是轨道。稳定的轨道都是椭圆形(圆形轨道就是一个偏心率为零的椭圆轨道)。如果其切线速度大于逃逸速度,那么它的轨道就成为抛物线或双曲线轨道。
- 比冲(specific impulse, Isp)
- 比冲 Isp 是对一个推进系统的燃烧效率的描述。比冲越高,单位燃料所产生的推力越大。通常比冲的单位可以用秒来表示,不过其正确的物理学单位为 距离每单位时间,通常用 米每秒 或 英尺每秒。为避免与速度的单位混淆,物理学上会把比冲除以地球(或Kerbin)表面的重力加速度(9.81 m/s²)再使用。这样比冲的单位就是秒。在公式中实际使用比冲时,它必须转化为正确的物理学单位——距离每单位时间,即再乘以地球(或Kerbin)表面的重力加速度(9.81 m/s²)。这种比冲值只是为了单位的转换,比冲并不随引力的变化而变化。
- 比冲是推力和燃料流量的比值,所以有时候会以作为其单位。这只是另一种数学形式, ,而力是质量和加速度之乘积,即,所以在国际单位制下可以得到 。
- 作用范围(sphere of influence, SoI, SOI)
- 以该天体为主要引力源的球体范围。游戏中在特定天体的作用范围内的飞船只考虑该天体的引力。
- 切向速度(tangential velocity)
- 物体沿其飞行轨迹切线方向的速度分量。瞬时速度的方向永远是运动轨迹的切线方向。
- 轨迹(trajectory)
- 轨迹是运动物体以时间为变量所得到的空间位置所组成的路径。
- 速度(velocity)
- 位移随时间的变化率。速度是矢量,单位为米每秒(m/s)。
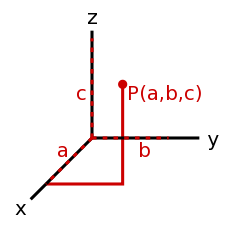
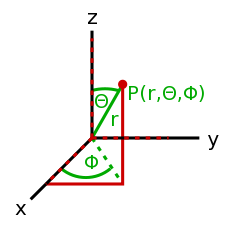







![I_{{sp}}={\frac {T}{{\dot m}}},[I_{{sp}}]={\frac {m}{s}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ff940eef93d9743a07d72ba2bb808e3b0372c36)



