Difference between revisions of "Tutorial: Basic Orbiting/fr"
m (→Stabiliser une orbite) |
SlayerGames (talk | contribs) m (Moved to /fr category) |
||
| (23 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
La différence d'altitude entre périastre et apoastre est caractérisée par l'''[http://fr.wikipedia.org/wiki/Excentricit%C3%A9_orbitale excentricité]'' de l'orbite. Une orbite très circulaire a une excentricité nulle et une orbite très elliptique a une excentricité proche de 1. | La différence d'altitude entre périastre et apoastre est caractérisée par l'''[http://fr.wikipedia.org/wiki/Excentricit%C3%A9_orbitale excentricité]'' de l'orbite. Une orbite très circulaire a une excentricité nulle et une orbite très elliptique a une excentricité proche de 1. | ||
| − | Vous trouverez facilement des calculateurs qui vous permettent de calculer tous les paramètres orbitaux et le <math>\Delta v</math> dont vous avez besoin pour vos manœuvres. | + | Vous trouverez facilement des calculateurs qui vous permettent de calculer tous les paramètres orbitaux et le <math>\Delta v</math> dont vous avez besoin pour vos manœuvres. Que vous utilisiez un calculateur ou que vous calculiez vos orbites à la main, le mode opératoire est le même que celui explosé ci-dessous. |
Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante : | Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante : | ||
| − | <math>v = \sqrt{\mu\left(\frac{2}{r}-\frac{1}{a}\right)}</math> | + | :<math>v = \sqrt{\mu\left(\frac{2}{r}-\frac{1}{a}\right)}</math> |
Où | Où | ||
| Line 24: | Line 24: | ||
Rappelez-vous qu'en effectuant une manœuvre à une des extrémités de l'orbite, vous entraînerez une changement d'altitude de l'''autre'' extrémité. Par exemple, si vous êtes au périastre (au plus bas, vitesse maximale) et que vous poussez dans la direction pro-grade (pour prendre de la vitesse), l'apoastre va prendre de l'altitude. Au contraire si vous poussez dans la direction rétrograde, votre apoastre va baisser. | Rappelez-vous qu'en effectuant une manœuvre à une des extrémités de l'orbite, vous entraînerez une changement d'altitude de l'''autre'' extrémité. Par exemple, si vous êtes au périastre (au plus bas, vitesse maximale) et que vous poussez dans la direction pro-grade (pour prendre de la vitesse), l'apoastre va prendre de l'altitude. Au contraire si vous poussez dans la direction rétrograde, votre apoastre va baisser. | ||
| − | En pratique, pour circulariser votre orbite depuis l'apoastre, vous devez prendre de la vitesse. Pointez le nez de la fusée dans la direction pro-grade (cible jaune sans la croix sur la Navball) et allumez les moteurs. Appuyez sur "M" pour passer en mode carte et | + | En pratique, pour circulariser votre orbite depuis l'apoastre, vous devez prendre de la vitesse. Pointez le nez de la fusée dans la direction pro-grade (cible jaune sans la croix sur la [[Navball/fr|Navball]]) et allumez les moteurs. Appuyez sur "M" pour passer en mode carte et surveillez l'évolution de votre périastre (qui est en train de monter). Quand apoastre et périastre s'inversent sur votre orbite, coupez les moteurs (touche "X"). Votre orbite est maintenant circulaire. Le moment ou les points s'inversent est très court, entraînez-vous à couper les moteurs au bon moment. |
Au contraire si vous voulez circulariser votre orbite depuis le périastre, vous devrez perdre de la vitesse. Orientez le vaisseau dans la direction rétrograde (cible jaune avec croix centrale) et effectuez la même opération. | Au contraire si vous voulez circulariser votre orbite depuis le périastre, vous devrez perdre de la vitesse. Orientez le vaisseau dans la direction rétrograde (cible jaune avec croix centrale) et effectuez la même opération. | ||
Il est périlleux d'effectuer cette manœuvre en un autre point quelconque de l'orbite car cela va modifier ''à la fois'' votre apoastre et votre périastre. Par ailleurs, lors de l'injection en orbite de [[Kerbin]], la poussée est très longue et ne peut se faire uniquement à l'apoastre, ce qui entraîne une difficulté à faire une orbite ronde du premier coup. Néanmoins, si vous calculez la vitesse que vous voulez attendre, vous pouvez laisser vos moteurs allumés jusqu'à être à la bonne vitesse et vous garantir un orbite ronde (si vous êtes pile à la bonne altitude, bonne chance). | Il est périlleux d'effectuer cette manœuvre en un autre point quelconque de l'orbite car cela va modifier ''à la fois'' votre apoastre et votre périastre. Par ailleurs, lors de l'injection en orbite de [[Kerbin]], la poussée est très longue et ne peut se faire uniquement à l'apoastre, ce qui entraîne une difficulté à faire une orbite ronde du premier coup. Néanmoins, si vous calculez la vitesse que vous voulez attendre, vous pouvez laisser vos moteurs allumés jusqu'à être à la bonne vitesse et vous garantir un orbite ronde (si vous êtes pile à la bonne altitude, bonne chance). | ||
| − | == | + | == Orbite de transfert == |
| − | + | La manière la plus efficace de passer d'une orbite circulaire à une autre orbite circulaire plus élevée (ou plus basse) est d'utiliser une orbite de transfert elliptique, appelée [http://fr.wikipedia.org/wiki/Orbite_de_transfert orbite de Hohmann]. Le principe est de modifier notre orbite initiale afin que l'altitude de l'autre extrémité vaille le rayon de l'orbite finale. Ensuite, on patiente jusqu'à atteindre ce point, où on circularise l'orbite. | |
| + | Par exemple pour passer d'une orbite de 100 km à une orbite de 200 km, on effectue une poussé pro-grade et on fait monter notre apoastre à 200 km. Lorsqu'on atteint ce nouvel apoastre, on effectue une autre poussée pro-grade pour faire monter notre périastre à 200 km. Le principe est le même, bien qu'inversé, pour passer à orbite circulaire moins élevée. | ||
| − | === | + | === Vitesse cible === |
| − | + | La clé des orbites de transfert est de connaître la vitesse qu'il faut prendre ou perdre (le <math>\Delta v</math>) pour atteindre l'altitude désirée. Pour ce faire, on utilise cette formule, qui découle directement de la formule donnée plus haut. | |
| − | <math>v = | + | :<math>v = \sqrt{\mu \cdot \left(\frac{2}{r_i} - \frac{2}{(r_i+r_f)}\right)}</math> |
| − | + | Où <math>r_i</math> et <math>r_f</math> sont les rayons des orbites initiale et finale. | |
| − | + | La différence entre votre vitesse actuelle et la vitesse calculée vous donne directement le <math>\Delta v</math> (négatif ou positif) à appliquer pour passer sur l'orbite de transfert. | |
| + | Rappelez-vous que vous devrez refaire une poussée à la fin du transfert. Le <math>\Delta v</math> de cette manœuvre se calcule grâce à la même première formule. On note que dans ce cas, la formule peut être simplifiée car on recherche la vitesse d'une orbite circulaire (constante) et dans ce cas, <math>r=a</math> et la formule devient | ||
| − | = | + | :<math>v = \sqrt{\frac{\mu}{r}}</math> |
| − | |||
| − | === R | + | Faites attention aux unités. Si vous utilisez les unités standards pour <math>\mu</math> (des <math>m^3/s^2</math>) ne mettez pas <math>r</math> en <math>km</math>, mais bien en <math>m</math>, sinon vous obtiendrez une réponse complètement fausse. Vous pouvez transformer toutes vos valeurs en utilisant des kilomètres et, par exemple, des heures, et vous obtiendrez une valeur de <math>v</math> en <math>km/h</math> au lieu de <math>m/s</math>. Une façon simple de savoir si tout est correct est de vérifier si vos résultats ont un sens. La vitesse orbitale autour de Kerbin (LKO) est d'environ <math>2 km/s</math>. Si vous trouvez <math>2000km/s</math> ou <math>2m/s</math>, il y a un problème quelque part... |
| + | |||
| + | Pensez aussi toujours que quand on parle de rayon d'orbite, on parle de distance au '''centre''' du corps orbité, ce qui représente la somme du rayon du corps et de l'altitude de l'orbite. | ||
| + | |||
| + | === Désorbitation === | ||
| + | |||
| + | La manière la plus simple et la plus économique de se désorbiter depuis n'importe quelle altitude est d'injecter le véhicule sur une orbite de transfert descendante dont le périastre est inférieur à 70 000 m (c'est-à-dire dans l'atmosphère de [[Kerbin]], qui diffère évidement en fonction des planètes). Mais comme l'atmosphère est très fine à haute altitude, la traverser ne vous fera pas ralentir assez que pour abaisser suffisamment votre apoastre en un seul passage et plusieurs orbites seront nécessaires pour vous désorbiter. Si vous êtes à court de carburant ou si vous avez le temps (sonde non habitée, par exemple), c'est un très bon compromis. Si vous voulez vous désorbiter en un seul passage, visez plutôt une altitude sous les 30 000 m, ce qui vous coûtera plus de carburant. | ||
| + | |||
| + | Si vous voulez vous poser sur un corps dépourvu d'atmosphère (comme la [[Mun]]), vous devrez ramener l'altitude de votre périastre à zéro sous peine de reprendre de l'altitude aussitôt, puis freiner avec vos moteurs pour ne pas percuter la surface à une vitesse suicidaire (sauf si c'est ce que vous cherchez). | ||
| + | |||
| + | === Code R pour planifier une orbite de transfert de hohmann === | ||
hohmann <- function(from_alt,to_alt){ | hohmann <- function(from_alt,to_alt){ | ||
| Line 67: | Line 78: | ||
return(out)} | return(out)} | ||
| − | ==== | + | ==== Exemple ==== |
| − | + | Voici un graphe montrant les vitesses nécessaires pour passer de différentes altitudes d'orbite circulaire à des orbites de ré-entrée. | |
| − | |||
plot(100*1:40,1000*hohmann(100*1:40,34)$b1$to,main="Landing speeds",xlab="altitude (km)",ylab="speed (m/s)") | plot(100*1:40,1000*hohmann(100*1:40,34)$b1$to,main="Landing speeds",xlab="altitude (km)",ylab="speed (m/s)") | ||
| Line 75: | Line 85: | ||
[[File:landingspeeds.png]] | [[File:landingspeeds.png]] | ||
| − | R | + | Lien vers le R Project (en) [http://www.r-project.org/] |
| + | |||
| + | === Table des vitesses orbitales autour de Kerbin === | ||
| + | '''Note''' : l'atmosphère de [[Kerbin]] présentait auparavant un limite nette à 34,5 km d'altitude mais s'étend actuellement jusqu'environ 68 km. Sous cette altitude, votre orbite va se dégrader graduellement. La dégradation devient rapide sous les 45 km. Les orbites inférieures à 68 km sont données à titre d'information mais ne peuvent évidement être maintenues sans corrections régulière pour maintenir la vitesse orbitale déteriorée par la traînée atmosphérique. | ||
| − | |||
| − | |||
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
! Altitude (m) | ! Altitude (m) | ||
| − | ! | + | ! Vitesse horizontale (m/s) |
| − | ! | + | ! Période orbitale (min) |
|- | |- | ||
| − | | | + | | 40 000 || 2348,7 || 28,54 |
|- | |- | ||
| − | | | + | | 50 000 || 2330,6 || 29,21 |
|- | |- | ||
| − | | | + | | 60 000 || 2312,8 || 29,88 |
|- | |- | ||
| − | | | + | | 70 000 || 2295,5 || 30,56 |
|- | |- | ||
| − | | | + | | 80 000 || 2278,6 || 31,25 |
|- | |- | ||
| − | | | + | | 85 000 || 2270,3 || 31,60 |
|- | |- | ||
| − | | | + | | 90 000 || 2262,0 || 31,94 |
|- | |- | ||
| − | | | + | | 10 0000 || 2245,8 || 32,64 |
|- | |- | ||
| − | | | + | | 110 000 || 2229,9 || 33,34 |
|- | |- | ||
| − | | | + | | 120 000 || 2214,4 || 34,05 |
|- | |- | ||
| − | | | + | | 130 000 || 2199,2 || 34,76 |
|- | |- | ||
| − | | | + | | 140 000 || 2184,3 || 35,48 |
|- | |- | ||
| − | | | + | | 150 000 || 2169,6 || 36,20 |
|- | |- | ||
| − | | | + | | 160 000 || 2155,3 || 36,93 |
|- | |- | ||
| − | | | + | | 170 000 || 2141,3 || 37,66 |
|- | |- | ||
| − | | | + | | 180 000 || 2127,5 || 38,39 |
|- | |- | ||
| − | | | + | | 190 000 || 2114,0 || 39,13 |
|- | |- | ||
| − | | | + | | 200 000 || 2100,7 || 39,88 |
|- | |- | ||
| − | | | + | | 210 000 || 2087,7 || 40,63 |
|- | |- | ||
| − | | | + | | 220 000 || 2075,0 || 41,38 |
|- | |- | ||
| − | | | + | | 230 000 || 2062,4 || 42,14 |
|- | |- | ||
| − | | | + | | 240 000 || 2050,1 || 42,91 |
|- | |- | ||
| − | | | + | | 250 000 || 2038,0 || 43,68 |
|- | |- | ||
| − | | | + | | 260 000 || 2026,1 || 44,45 |
|- | |- | ||
| − | | | + | | 270 000 || 2014,5 || 45,23 |
|- | |- | ||
| − | | | + | | 280 000 || 2003,0 || 46,01 |
|- | |- | ||
| − | | | + | | 290 000 || 1991,7 || 46,79 |
|- | |- | ||
| − | | | + | | 300 000 || 1980,6 || 47,59 |
|- | |- | ||
| − | | | + | | 310 000 || 1969,7 || 48,38 |
|- | |- | ||
| − | | | + | | 320 000 || 1959,0 || 49,18 |
|- | |- | ||
| − | | | + | | 330 000 || 1948,4 || 49,98 |
|- | |- | ||
| − | | | + | | 340 000 || 1938,0 || 50,79 |
|- | |- | ||
| − | | | + | | 350 000 || 1927,8 || 51,61 |
|- | |- | ||
| − | | | + | | 360 000 || 1917,7 || 52,42 |
|- | |- | ||
| − | | | + | | 370 000 || 1907,8 || 53,24 |
|- | |- | ||
| − | | | + | | 380 000 || 1898,0 || 54,07 |
|- | |- | ||
| − | | | + | | 390 000 || 1888,4 || 54,90 |
|- | |- | ||
| − | | | + | | 400 000 || 1879,0 || 55,73 |
|- | |- | ||
| − | | | + | | 410 000 || 1869,6 || 56,57 |
|- | |- | ||
| − | | | + | | 420 000 || 1860,5 || 57,41 |
|- | |- | ||
| − | | | + | | 430 000 || 1851,4 || 58,26 |
|- | |- | ||
| − | | | + | | 440 000 || 1842,5 || 59,11 |
|- | |- | ||
| − | | | + | | 450 000 || 1833,7 || 59,96 |
|- | |- | ||
| − | | | + | | 460 000 || 1825,0 || 60,82 |
|- | |- | ||
| − | | | + | | 470 000 || 1816,5 || 61,69 |
|- | |- | ||
| − | | | + | | 480 000 || 1808,0 || 62,55 |
|- | |- | ||
| − | | | + | | 490 000 || 1799,7 || 63,42 |
|- | |- | ||
| − | | | + | | 500 000 || 1791,5 || 64,30 |
|- | |- | ||
| − | | | + | | 510 000 || 1783,4 || 65,18 |
|- | |- | ||
| − | | | + | | 520 000 || 1775,5 || 66,06 |
|- | |- | ||
| − | | | + | | 530 000 || 1767,6 || 66,95 |
|- | |- | ||
| − | | | + | | 540 000 || 1759,8 || 67,84 |
|- | |- | ||
| − | | | + | | 550 000 || 1752,1 || 68,73 |
|- | |- | ||
| − | | | + | | 560 000 || 1744,6 || 69,63 |
|- | |- | ||
| − | | | + | | 570 000 || 1737,1 || 70,53 |
|- | |- | ||
| − | | | + | | 580 000 || 1729,7 || 71,44 |
|- | |- | ||
| − | | | + | | 590 000 || 1722,4 || 72,35 |
|- | |- | ||
| − | | | + | | 600 000 || 1715,3 || 73,26 |
|- | |- | ||
| − | | | + | | 610 000 || 1708,2 || 74,18 |
|- | |- | ||
| − | | | + | | 620 000 || 1701,1 || 75,10 |
|- | |- | ||
| − | | | + | | 630 000 || 1694,2 || 76,03 |
|- | |- | ||
| − | | | + | | 640 000 || 1687,4 || 76,96 |
|- | |- | ||
| − | | | + | | 650 000 || 1680,6 || 77,89 |
|- | |- | ||
| − | | | + | | 660 000 || 1673,9 || 78,83 |
|- | |- | ||
| − | | | + | | 670 000 || 1667,3 || 79,77 |
|- | |- | ||
| − | | | + | | 680 000 || 1660,8 || 80,71 |
|- | |- | ||
| − | | | + | | 690 000 || 1654,3 || 81,66 |
|- | |- | ||
| − | | | + | | 700 000 || 1648,0 || 82,61 |
|- | |- | ||
| − | | | + | | 710 000 || 1641,7 || 83,56 |
|- | |- | ||
| − | | | + | | 720 000 || 1635,4 || 84,52 |
|- | |- | ||
| − | | | + | | 730 000 || 1629,3 || 85,48 |
|- | |- | ||
| − | | | + | | 740 000 || 1623,2 || 86,45 |
|- | |- | ||
| − | | | + | | 750 000 || 1617,2 || 87,42 |
|- | |- | ||
| − | | | + | | 760 000 || 1611,2 || 88,39 |
|- | |- | ||
| − | | | + | | 770 000 || 1605,3 || 89,37 |
|- | |- | ||
| − | | | + | | 780 000 || 1599,5 || 90,35 |
|- | |- | ||
| − | | | + | | 790 000 || 1593,7 || 91,33 |
|- | |- | ||
| − | | | + | | 800 000 || 1588,0 || 92,32 |
|- | |- | ||
| − | | | + | | 810 000 || 1582,4 || 93,31 |
|- | |- | ||
| − | | | + | | 820 000 || 1576,8 || 94,31 |
|- | |- | ||
| − | | | + | | 830 000 || 1571,3 || 95,30 |
|- | |- | ||
| − | | | + | | 840 000 || 1565,8 || 96,31 |
|- | |- | ||
| − | | | + | | 850 000 || 1560,4 || 97,31 |
|- | |- | ||
| − | | | + | | 860 000 || 1555,0 || 98,32 |
|- | |- | ||
| − | | | + | | 870 000 || 1549,7 || 99,33 |
|- | |- | ||
| − | | | + | | 880 000 || 1544,5 || 100,35 |
|- | |- | ||
| − | | | + | | 885 000 || 1541,9 || 100,86 |
|- | |- | ||
| − | | | + | | 890 000 || 1539,3 || 101,37 |
|- | |- | ||
| − | | | + | | 900 000 || 1534,2 || 102,39 |
|- | |- | ||
| − | | | + | | 910 000 || 1529,1 || 103,41 |
|- | |- | ||
| − | | | + | | 920 000 || 1524,0 || 104,44 |
|- | |- | ||
| − | | | + | | 930 000 || 1519,1 || 105,47 |
|- | |- | ||
| − | | | + | | 940 000 || 1514,1 || 106,51 |
|- | |- | ||
| − | | | + | | 950 000 || 1509,2 || 107,55 |
|- | |- | ||
| − | | | + | | 960 000 || 1504,4 || 108,59 |
|- | |- | ||
| − | | | + | | 970 000 || 1499,6 || 109,64 |
|- | |- | ||
| − | | | + | | 980 000 || 1494,8 || 110,69 |
|- | |- | ||
| − | | | + | | 990 000 || 1490,1 || 111,74 |
|- | |- | ||
| − | | | + | | 1 000 000 || 1485,5 || 112,79 |
|- | |- | ||
| − | | 2 868 378 || 1008 | + | | 2 868 378 || 1008,910 || 6 hours |
|- | |- | ||
| − | | 8 140 000 || 635 | + | | 8 140 000 || 635,4 || 24 hours |
|} | |} | ||
| − | + | ||
| − | [[Category:Tutorials| | + | |
| + | [[Category:Tutorials/fr|Basic Orbiting (Technical)]] | ||
Latest revision as of 18:49, 2 May 2019
Aller dans l'espace est relativement simple, mais y rester sans retomber au sol ou dériver sans fin dans l'espace est une autre paire de manches. Ce tutoriel vous expliquera comment procéder à une mise en orbite et à y rester, comment circulariser votre orbite ou créer une orbite elliptique et comment diminuer ou augmenter votre orbite.
Contents
Stabiliser une orbite
Lors d'une orbite, votre vaisseau va atteindre une altitude maximale, l''apoastre, et une altitude minimale, le périastre, diamétralement opposés l'un à l'autre. En ces deux points, la vitesse verticale (par rapport à la surface) est nulle, on peut donc aisément calculer notre vitesse orbitale (qui est la même que la vitesse surface). C'est en ces deux endroits qu'il est le plus facile (et le moins coûteux en carburant) de faire des corrections de trajectoire afin de modifier l'orbite. La différence d'altitude entre périastre et apoastre est caractérisée par l'excentricité de l'orbite. Une orbite très circulaire a une excentricité nulle et une orbite très elliptique a une excentricité proche de 1.
Vous trouverez facilement des calculateurs qui vous permettent de calculer tous les paramètres orbitaux et le dont vous avez besoin pour vos manœuvres. Que vous utilisiez un calculateur ou que vous calculiez vos orbites à la main, le mode opératoire est le même que celui explosé ci-dessous.
Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante :
Où
- est un paramètre gravitationnel du corps orbité (3530,461 km³/s² pour Kerbin).
- est la constante gravitationnelle ().
- est la masse du corps orbité.
- est votre distance au centre du corps que vous orbitez (c'est-à-dire la somme du rayon de la planète et de votre altitude)
- est le demi-grand axe de votre orbite (qui est la demi-somme des altitudes de vos périastre et apoastre et du diamètre de la planète).
Plus votre altitude est grande, moins vous êtes attirés par Kerbin (le corps orbité), moins votre vitesse doit être élevée pour rester dans une orbite circulaire. Vous pouvez calculer la vitesse appropriée à l'apoastre ou périastre de votre ellipse pour obtenir une orbite circulaire à cette altitude. Connaissant votre vitesse effective à ce point de votre ellipse, vous pouvez calculer de combien vous devez modifier votre vitesse pour obtenir une orbite circulaire. Pour ce faire, vous pouvez utiliser la formule ci-dessus, un calculateur ou une table (voir en fin d'article).
Rappelez-vous qu'en effectuant une manœuvre à une des extrémités de l'orbite, vous entraînerez une changement d'altitude de l'autre extrémité. Par exemple, si vous êtes au périastre (au plus bas, vitesse maximale) et que vous poussez dans la direction pro-grade (pour prendre de la vitesse), l'apoastre va prendre de l'altitude. Au contraire si vous poussez dans la direction rétrograde, votre apoastre va baisser.
En pratique, pour circulariser votre orbite depuis l'apoastre, vous devez prendre de la vitesse. Pointez le nez de la fusée dans la direction pro-grade (cible jaune sans la croix sur la Navball) et allumez les moteurs. Appuyez sur "M" pour passer en mode carte et surveillez l'évolution de votre périastre (qui est en train de monter). Quand apoastre et périastre s'inversent sur votre orbite, coupez les moteurs (touche "X"). Votre orbite est maintenant circulaire. Le moment ou les points s'inversent est très court, entraînez-vous à couper les moteurs au bon moment. Au contraire si vous voulez circulariser votre orbite depuis le périastre, vous devrez perdre de la vitesse. Orientez le vaisseau dans la direction rétrograde (cible jaune avec croix centrale) et effectuez la même opération. Il est périlleux d'effectuer cette manœuvre en un autre point quelconque de l'orbite car cela va modifier à la fois votre apoastre et votre périastre. Par ailleurs, lors de l'injection en orbite de Kerbin, la poussée est très longue et ne peut se faire uniquement à l'apoastre, ce qui entraîne une difficulté à faire une orbite ronde du premier coup. Néanmoins, si vous calculez la vitesse que vous voulez attendre, vous pouvez laisser vos moteurs allumés jusqu'à être à la bonne vitesse et vous garantir un orbite ronde (si vous êtes pile à la bonne altitude, bonne chance).
Orbite de transfert
La manière la plus efficace de passer d'une orbite circulaire à une autre orbite circulaire plus élevée (ou plus basse) est d'utiliser une orbite de transfert elliptique, appelée orbite de Hohmann. Le principe est de modifier notre orbite initiale afin que l'altitude de l'autre extrémité vaille le rayon de l'orbite finale. Ensuite, on patiente jusqu'à atteindre ce point, où on circularise l'orbite. Par exemple pour passer d'une orbite de 100 km à une orbite de 200 km, on effectue une poussé pro-grade et on fait monter notre apoastre à 200 km. Lorsqu'on atteint ce nouvel apoastre, on effectue une autre poussée pro-grade pour faire monter notre périastre à 200 km. Le principe est le même, bien qu'inversé, pour passer à orbite circulaire moins élevée.
Vitesse cible
La clé des orbites de transfert est de connaître la vitesse qu'il faut prendre ou perdre (le ) pour atteindre l'altitude désirée. Pour ce faire, on utilise cette formule, qui découle directement de la formule donnée plus haut.
Où et sont les rayons des orbites initiale et finale.
La différence entre votre vitesse actuelle et la vitesse calculée vous donne directement le (négatif ou positif) à appliquer pour passer sur l'orbite de transfert. Rappelez-vous que vous devrez refaire une poussée à la fin du transfert. Le de cette manœuvre se calcule grâce à la même première formule. On note que dans ce cas, la formule peut être simplifiée car on recherche la vitesse d'une orbite circulaire (constante) et dans ce cas, et la formule devient
Faites attention aux unités. Si vous utilisez les unités standards pour (des ) ne mettez pas en , mais bien en , sinon vous obtiendrez une réponse complètement fausse. Vous pouvez transformer toutes vos valeurs en utilisant des kilomètres et, par exemple, des heures, et vous obtiendrez une valeur de en au lieu de . Une façon simple de savoir si tout est correct est de vérifier si vos résultats ont un sens. La vitesse orbitale autour de Kerbin (LKO) est d'environ . Si vous trouvez ou , il y a un problème quelque part...
Pensez aussi toujours que quand on parle de rayon d'orbite, on parle de distance au centre du corps orbité, ce qui représente la somme du rayon du corps et de l'altitude de l'orbite.
Désorbitation
La manière la plus simple et la plus économique de se désorbiter depuis n'importe quelle altitude est d'injecter le véhicule sur une orbite de transfert descendante dont le périastre est inférieur à 70 000 m (c'est-à-dire dans l'atmosphère de Kerbin, qui diffère évidement en fonction des planètes). Mais comme l'atmosphère est très fine à haute altitude, la traverser ne vous fera pas ralentir assez que pour abaisser suffisamment votre apoastre en un seul passage et plusieurs orbites seront nécessaires pour vous désorbiter. Si vous êtes à court de carburant ou si vous avez le temps (sonde non habitée, par exemple), c'est un très bon compromis. Si vous voulez vous désorbiter en un seul passage, visez plutôt une altitude sous les 30 000 m, ce qui vous coûtera plus de carburant.
Si vous voulez vous poser sur un corps dépourvu d'atmosphère (comme la Mun), vous devrez ramener l'altitude de votre périastre à zéro sous peine de reprendre de l'altitude aussitôt, puis freiner avec vos moteurs pour ne pas percuter la surface à une vitesse suicidaire (sauf si c'est ce que vous cherchez).
Code R pour planifier une orbite de transfert de hohmann
hohmann <- function(from_alt,to_alt){
# provides information needed to perform
# a hohmann transfer from a circular ortbit
# at from_alt (km) to a circular orbit at to_alt (km)
mu <- 3530.394 # Gravitational parameter (km^3/s^2)
R <- 600 # Kerbin radius (km)
r1 <- from_alt+R # radius 1 (km)
r2 <- to_alt+R # radius 2 (km)
vc1 <- sqrt(mu/r1) # circular orbit velocity 1 (km/s)
vc2 <- sqrt(mu/r2) # circular orbit velocity 2 (km/s)
a <- (r1+r2)/2 # semi-major axis of transfer orbit (km)
T <- 2*pi*sqrt((a^3)/mu) # period of transfer orbit (s)
dv1 <- (sqrt(r2/a)-1)*vc1 # delta v1 (km/s)
dv2 <- (1-sqrt(r1/a))*vc2 # delta v2 (km/s)
b1 <- list(from=vc1,to=vc1+dv1) # burn one from-to velocities (km/s)
t <- T/2 # time between burns (s)
b2 <- list(from=vc2+dv2,to=vc2) # burn two from-to velocities (km/s)
out <- list(from_alt=from_alt,b1=b1,t=t,b2=b2,to_alt=to_alt)
return(out)}
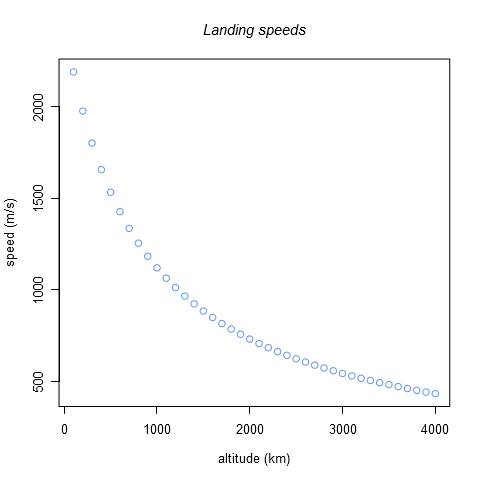
Exemple
Voici un graphe montrant les vitesses nécessaires pour passer de différentes altitudes d'orbite circulaire à des orbites de ré-entrée.
plot(100*1:40,1000*hohmann(100*1:40,34)$b1$to,main="Landing speeds",xlab="altitude (km)",ylab="speed (m/s)")
Lien vers le R Project (en) [1]
Table des vitesses orbitales autour de Kerbin
Note : l'atmosphère de Kerbin présentait auparavant un limite nette à 34,5 km d'altitude mais s'étend actuellement jusqu'environ 68 km. Sous cette altitude, votre orbite va se dégrader graduellement. La dégradation devient rapide sous les 45 km. Les orbites inférieures à 68 km sont données à titre d'information mais ne peuvent évidement être maintenues sans corrections régulière pour maintenir la vitesse orbitale déteriorée par la traînée atmosphérique.
| Altitude (m) | Vitesse horizontale (m/s) | Période orbitale (min) |
|---|---|---|
| 40 000 | 2348,7 | 28,54 |
| 50 000 | 2330,6 | 29,21 |
| 60 000 | 2312,8 | 29,88 |
| 70 000 | 2295,5 | 30,56 |
| 80 000 | 2278,6 | 31,25 |
| 85 000 | 2270,3 | 31,60 |
| 90 000 | 2262,0 | 31,94 |
| 10 0000 | 2245,8 | 32,64 |
| 110 000 | 2229,9 | 33,34 |
| 120 000 | 2214,4 | 34,05 |
| 130 000 | 2199,2 | 34,76 |
| 140 000 | 2184,3 | 35,48 |
| 150 000 | 2169,6 | 36,20 |
| 160 000 | 2155,3 | 36,93 |
| 170 000 | 2141,3 | 37,66 |
| 180 000 | 2127,5 | 38,39 |
| 190 000 | 2114,0 | 39,13 |
| 200 000 | 2100,7 | 39,88 |
| 210 000 | 2087,7 | 40,63 |
| 220 000 | 2075,0 | 41,38 |
| 230 000 | 2062,4 | 42,14 |
| 240 000 | 2050,1 | 42,91 |
| 250 000 | 2038,0 | 43,68 |
| 260 000 | 2026,1 | 44,45 |
| 270 000 | 2014,5 | 45,23 |
| 280 000 | 2003,0 | 46,01 |
| 290 000 | 1991,7 | 46,79 |
| 300 000 | 1980,6 | 47,59 |
| 310 000 | 1969,7 | 48,38 |
| 320 000 | 1959,0 | 49,18 |
| 330 000 | 1948,4 | 49,98 |
| 340 000 | 1938,0 | 50,79 |
| 350 000 | 1927,8 | 51,61 |
| 360 000 | 1917,7 | 52,42 |
| 370 000 | 1907,8 | 53,24 |
| 380 000 | 1898,0 | 54,07 |
| 390 000 | 1888,4 | 54,90 |
| 400 000 | 1879,0 | 55,73 |
| 410 000 | 1869,6 | 56,57 |
| 420 000 | 1860,5 | 57,41 |
| 430 000 | 1851,4 | 58,26 |
| 440 000 | 1842,5 | 59,11 |
| 450 000 | 1833,7 | 59,96 |
| 460 000 | 1825,0 | 60,82 |
| 470 000 | 1816,5 | 61,69 |
| 480 000 | 1808,0 | 62,55 |
| 490 000 | 1799,7 | 63,42 |
| 500 000 | 1791,5 | 64,30 |
| 510 000 | 1783,4 | 65,18 |
| 520 000 | 1775,5 | 66,06 |
| 530 000 | 1767,6 | 66,95 |
| 540 000 | 1759,8 | 67,84 |
| 550 000 | 1752,1 | 68,73 |
| 560 000 | 1744,6 | 69,63 |
| 570 000 | 1737,1 | 70,53 |
| 580 000 | 1729,7 | 71,44 |
| 590 000 | 1722,4 | 72,35 |
| 600 000 | 1715,3 | 73,26 |
| 610 000 | 1708,2 | 74,18 |
| 620 000 | 1701,1 | 75,10 |
| 630 000 | 1694,2 | 76,03 |
| 640 000 | 1687,4 | 76,96 |
| 650 000 | 1680,6 | 77,89 |
| 660 000 | 1673,9 | 78,83 |
| 670 000 | 1667,3 | 79,77 |
| 680 000 | 1660,8 | 80,71 |
| 690 000 | 1654,3 | 81,66 |
| 700 000 | 1648,0 | 82,61 |
| 710 000 | 1641,7 | 83,56 |
| 720 000 | 1635,4 | 84,52 |
| 730 000 | 1629,3 | 85,48 |
| 740 000 | 1623,2 | 86,45 |
| 750 000 | 1617,2 | 87,42 |
| 760 000 | 1611,2 | 88,39 |
| 770 000 | 1605,3 | 89,37 |
| 780 000 | 1599,5 | 90,35 |
| 790 000 | 1593,7 | 91,33 |
| 800 000 | 1588,0 | 92,32 |
| 810 000 | 1582,4 | 93,31 |
| 820 000 | 1576,8 | 94,31 |
| 830 000 | 1571,3 | 95,30 |
| 840 000 | 1565,8 | 96,31 |
| 850 000 | 1560,4 | 97,31 |
| 860 000 | 1555,0 | 98,32 |
| 870 000 | 1549,7 | 99,33 |
| 880 000 | 1544,5 | 100,35 |
| 885 000 | 1541,9 | 100,86 |
| 890 000 | 1539,3 | 101,37 |
| 900 000 | 1534,2 | 102,39 |
| 910 000 | 1529,1 | 103,41 |
| 920 000 | 1524,0 | 104,44 |
| 930 000 | 1519,1 | 105,47 |
| 940 000 | 1514,1 | 106,51 |
| 950 000 | 1509,2 | 107,55 |
| 960 000 | 1504,4 | 108,59 |
| 970 000 | 1499,6 | 109,64 |
| 980 000 | 1494,8 | 110,69 |
| 990 000 | 1490,1 | 111,74 |
| 1 000 000 | 1485,5 | 112,79 |
| 2 868 378 | 1008,910 | 6 hours |
| 8 140 000 | 635,4 | 24 hours |