Difference between revisions of "Terminology/zh-tw"
From Kerbal Space Program Wiki
(→軌道) |
|||
| Line 71: | Line 71: | ||
;<span id="ecc">離心率(eccentricity)</span> | ;<span id="ecc">離心率(eccentricity)</span> | ||
| − | < | + | <math style="float:right;padding:0.5em;">\text{ecc} = 1 - \frac{2}{\frac{Ap}{Pe}+1}</math> |
:描述軌道幾何特徵的參數。 | :描述軌道幾何特徵的參數。 | ||
| Line 137: | Line 137: | ||
;<span id="TWR">推重比(thrust-weight-ratio,TWR)</span> | ;<span id="TWR">推重比(thrust-weight-ratio,TWR)</span> | ||
| − | :< | + | :<math style="float:right;padding:.5em;">\text{TWR} = \frac{T}{W} =\frac{T}{m \cdot g}</math>飛船總質量與動力段所有發動機總推力的比值。若TWR>1,飛船可以完成加速和上升。若TWR<1,飛船是無法克服重力和低飛行高度空氣阻力的,不過低TWR在太空或許可以足夠保證飛行器的運動。因為飛船重量(W)與其所處位置的重力加速度(g)成正比,TWR也跟具體位置有關。Mün表面的重力加速度只是Kerbin表面重力加速度的16.6%,因此,TWR<sub>Kerbin</sub> = 1相當於TWR<sub>Mün</sub> = 6。 |
---- | ---- | ||
Latest revision as of 00:22, 8 November 2014
KSP中使用了大量物理學和軌道飛行的術語,面對這些詞語時,非專業人員無疑是會異常困惑,更不要說還有大量的其他科學詞彙和縮寫了。
本頁就是一個相關術語簡潔的查詢表單,希望能幫助你順利的走上專業宇航員之路。
有用的術語
數學
- 橢圓(ellipse)
- 橢圓是圓錐曲線的一種,是距確定的兩點的距離之和恆定的一點的運動軌跡。
- 法向量(normal vector)
- 一條與平面垂直的向量。
- 標量(scalar)
- 一個沒有方向的數值。標量一般會有測量單位的後綴,表明這個標量的量綱。比如3 米每秒(m/s),3 米(m),3 秒(s) 都是標量:它們分別是速率(區分於速度)、路程(區分於位移)和時間的單位。
- 向量, 矢量(vector)
- 一個方向和大小的集合。比如前進方向和速率放在一起就是速度。一個向量如何被表示取決於採用的坐標系,以及多少個維度被使用。<35°, 12>是一個二維的極坐標向量,而<14,9, -20>則是一個三維笛卡爾(直角)坐標向量。也有其他的坐標系,但這些是最常用的
- <35°, 12>是一個12個單位長的箭頭,從原點(零點,角度在這裡沒有意義,因為這是一個沒有長度的點)出發,結束在一個與偏離極軸(通常是x軸,逆時針旋轉為正角度)35°的點。
- <14, 9, -20>是一個從原點(<0,0,0>)出發,在一個x坐標為14,y坐標為9,z坐標為20的點終止的箭頭。
- 使用直角坐標系的優點是你可以準確地知道向量的終止位置在哪裡,但是計算向量的長度則比較麻煩。而在極坐標系中,向量長度十分易得,終止位置卻較難得出。
- 速度、加速度、力、動量等物理量都是矢量。
一個三維坐標系需要:
- 一個原點。
- 3個單位向量。這些向量定義了沿著坐標軸的基本量度和坐標軸的方向。
- 3個標量,這可以是角度或坐標,用來描述坐標空間中的位置。
軌道
- 軌道遠點(apoapsis)
- 橢圓軌道上,距離軌道中心天體最遠的點。
- 軌道近點(periapsis)
- 橢圓軌道上,距離軌道中心天體最近的點。
- 近-* 和 遠-* (peri-* and apo-*)
- 談到軌道,我們通常都用具體的天體名稱來指明軌道中心。因此,在這個遊戲中,對於環繞Kerbin的軌道,我們會用近Kerbin點(Perikee,Perikerb)、遠Kerbin點(Apokee,Apokerb)這樣的名稱。
- 升交點(ascending node)
- 以中心天體為參考系,軌道開始向“北”運動的點。 “北”向,是參考軌道中心天體的坐標系。
- 降交點(descending node)
- 以中心天體為參考系,軌道開始向南運動的點。
- 離心率(eccentricity)
- 描述軌道幾何特徵的參數。
- ecc = 0 → 圓形軌道;
- 0 < ecc < 1 → 橢圓軌道;
- ecc = 1 → 拋物線軌道- 這是一種逃逸軌道;
- ecc > 1 → 雙曲線軌道- 這是另一種逃逸軌道;
- 軌道傾角(inclination)
- 軌道平面與參考平面的夾角。 (例如,90° 赤道平面傾角軌道就是所謂的極地軌道。)
- 近Kerbin軌道(low Kerbin orbit, LKO)
- 大多數天體的低軌道都存在於其重力範圍內。該軌道高度低,但是穩定(高於大氣層)。低軌道通常都是後續飛行的基礎,位於上升段和向其他最終的目的地出發之間,在軌道的任意點都可以進行飛船脫離軌道的點火推進。其優點就是抵達低軌道所需要的燃料是最少的。
- 天頂(zenith)
- 地面座標系統中“正上方”的點,也就是火箭在發射場等待發射時指向的點,亦即,“天空中最高的點”。
- 天底(nadir)
- “天頂”的反向點。
- 軌道點(orbital nodes)
- 軌道中的特定點,如近點、遠點,以及與其他軌道的交匯點等等。
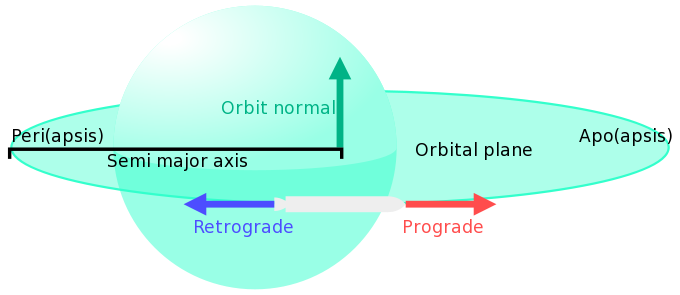
- 軌道法向(orbit normal)
- 軌道平面的正交方向矢量。飛船速度矢量方向與重力矢量方向的矢量和就是軌道法向。其遵照右手規則,飛船在軌道逆時針飛行時,其軌道法向朝“上”,順時針則朝下。而“上”也就是“北”,或“N+”,“下”也叫做“逆法向”,“南”或者“N-”。
- 軌道平面(orbital plane)
- 描述軌道環繞飛行平面的虛擬圓盤(通常用於表述軌道傾角)。
- 順行(prograde)
- 軌道路徑的前進方向。由於軌道為橢圓形,因此實際上它的方向是飛船所處軌道位置的切線方向。
- 逆行(retrograde)
- 順行的反向。
- 參考平面(reference plane)
- 所有飛行器在描述其所處軌道時都需要一個參考平面。對於行星軌道,通常是採用其赤道平面作為參照。類似太陽系的多天體平面為參考時,以黃道平面作為參考平面。在以其他軌道為目標飛行時,應採用目標軌道平面。軌道偏心率和上升點經度(以參考平面為坐標系)即可確定軌道平面。
- 半長軸(semi-major axis)
- 長軸是過焦點與橢圓相交的線長,而半長軸就是橢圓長軸的一半。在 KSP 中,半長軸的計算公式是:
。
軌道運行體的半長軸就是其中心橢圓軌道近點、遠點距離的平均值。由於軌道遠近點都是相對於軌道中心物體表面的距離,因此需要在公式中加入其半徑。半長軸相同的軌道運行週期相同,無論離心率如何。
- 亞軌道(sub-orbit)
- 亞軌道近點位於行星表面之下,亞軌道飛行最終會與該行星發生交會碰撞。
- 推重比(thrust-weight-ratio,TWR)
- 飛船總質量與動力段所有發動機總推力的比值。若TWR>1,飛船可以完成加速和上升。若TWR<1,飛船是無法克服重力和低飛行高度空氣阻力的,不過低TWR在太空或許可以足夠保證飛行器的運動。因為飛船重量(W)與其所處位置的重力加速度(g)成正比,TWR也跟具體位置有關。Mün表面的重力加速度只是Kerbin表面重力加速度的16.6%,因此,TWRKerbin = 1相當於TWRMün = 6。
太空機動
- 大氣層制動(atmospheric braking)
- → 全文: 空氣製動
- 降低軌道近點,使其進入行星的大氣層。這種飛行方式可以利用空氣阻力降低飛行器的速度。它可以用於再進入(參考下文),也可以應用於軌道的調整,同時節約燃料。
- 點火(burn)
- 點燃發動機,通常目的是進行軌道調整。
- 圓化調整(circularizing)
- 這種機動(發動機點火推進)的目的是把軌道的偏心率調整到近似於零。通常是在軌道近/遠點打開發動機推力來實現。
- 再入(re-entry)
- 就是再進入大氣層,並利用空氣阻力減速,使飛船進入地面返回軌道。由於需要足夠高的速度來避免大氣層把飛船“反彈”會太空,這種機動通常都會面臨著劇烈的升溫壓力。在目前的遊戲版本中,再進入過程只是個半成品,升溫和大氣反彈都沒有實現。(不過有相關的MOD實現這個特性)
- 反向點火(retroburn)
- 向飛船前進的反方向點火推進,例如,把發動機噴口轉向順行方向,飛船頭部對準逆行方向。這是一個常用的機動,可以在不改變其他軌道參數的情況下降低軌道速度。
物理
- 加速度(acceleration)
- 速度的改變率。加速度是矢量,單位為“米/秒2”(m/s2).
- 拋物線軌道(ballistic trajectory)
- 下落物體的軌道就是拋物線。在火箭飛行中,它就是指飛行器只受重力影響,本身沒有任何動力(如推力)的飛行軌道。
- 速度改變量(Δv, delta-v)
- 飛行器速度的實際改變量或可能改變量。測量單位為米每秒(m/s)。質量增大在單位時間內會降低Δv,而增加推力可以在單位時間內提高Δv。這是一個有效計算推進效率的參量。例如,飛行器脫離Kerbin大氣層並進入穩定軌道所需要的Δv大約是4,500 m/s。
- 能量(energy)
- 在軌飛行器的能量是其動能和勢能之和。勢能的計算公式是 ,動能的計算公式是 ,這裡G是萬有引力常量,M是行星的質量,m是飛行器的質量,R是距行星中心的距離,而v就是飛行器的速度。,總能量大於零,飛行器就進入逃逸軌道。相同半長軸的軌道能量相等。
- 逃逸速度(escape velocity)
- 脫離行星引力範圍所需要的速度,其計算公式為 ,G是萬有引力常量,M是行星的質量,r是行星半徑。
- g力(G-force)
- g力是一個加速度的量度,不過其考慮了重力的影響。地球海平面測量得到的重力加速度約為9.81 m/s²,將此定義為1G。地球表面物體的加速度大約都是1G。某物體如果其加速度為2G,其重力則增加一倍。在軌運行並關閉發動機的航天器處於自由落體狀態,此時為0G。
- 引力(gravity)
- 以物體的引力質量為力荷的力。本身非常微弱,只是那些質量很高的物體才能產生明顯的引力,如行星、月亮等。其大小與物體中心距離的平方呈反比。所以距離增加1倍,其引力會降低到1/22=1/4。
- 引力井(gravity wall)
- 行星引力的作用範圍。實際上這個區域是無限延伸的,但是由於引力會隨著距離的增大急劇降低,其範圍只是引力明顯起作用的區域。
- 當某物體具有足夠大的切線速度(而且其位於大氣層之外,無明顯的空氣阻力減速時),它會繞行星運行,並且不會落向該行星,這個運動軌跡就是軌道。穩定的軌道都是橢圓形(圓形軌道就是一個偏心率為零的橢圓軌道)。如果其切線速度大於逃逸速度,那麼它的軌道就成為拋物線或雙曲線軌道。
- 比衝(specific impulse,Isp)
- 比衝Isp 是對一個推進系統的燃燒效率的描述。比衝越高,單位燃料所產生的推力越大。通常比衝的單位可以用秒來表示,不過其正確的物理學單位為距離每單位時間,通常用米每秒 或英尺每秒。為避免與速度的單位混淆,物理學上會把比衝除以地球(或Kerbin)表面的重力加速度(9.81m/s²)再使用。這樣比衝的單位就是秒。在公式中實際使用比衝時,它必須轉化為正確的物理學單位——距離每單位時間,即再乘以地球(或Kerbin)表面的重力加速度(9.81 m/s²)。這種比沖值只是為了單位的轉換,比衝並不隨引力的變化而變化。
- 比衝是推力和燃料流量的比值,所以有時候會以作為其單位。這只是另一種數學形式, ,而力是質量和加速度之乘積,即,所以在國際單位制下可以得到。
- 作用範圍(sphere of influence, SoI, SOI)
- 以該天體為主要引力源的球體範圍。遊戲中在特定天體的作用範圍內的飛船隻考慮該天體的引力。
- 切向速度(tangential velocity)
- 物體沿其飛行軌跡切線方向的速度分量。瞬時速度的方向永遠是運動軌蹟的切線方向。
- 軌跡(trajectory)
- 軌跡是運動物體以時間為變量所得到的空間位置所組成的路徑。
- 速度(velocity)
- 位移隨時間的變化率。速度是矢量,單位為米每秒(m/s)。
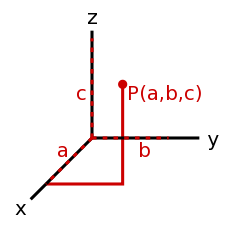
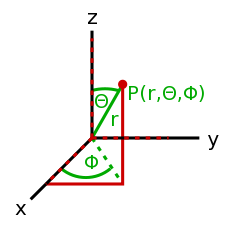







![{\displaystyle I_{sp}={\frac {T}{\dot {m}}},[I_{sp}]={\frac {m}{s}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ff940eef93d9743a07d72ba2bb808e3b0372c36)



