Difference between revisions of "Tutorial: Basic Orbiting/fr"
(→Stabiliser une orbite) |
(→Stabiliser une orbite) |
||
| Line 7: | Line 7: | ||
Vous trouverez facilement des calculateurs qui vous permettent de calculer tous les paramètres orbitaux et le <math>\Delta v</math> dont vous avez besoin pour vos manœuvres. que vous utilisiez un calculateur ou que vous calculiez vos orbites à la main, le mode opératoire est le même que celui explosé ci-dessous. | Vous trouverez facilement des calculateurs qui vous permettent de calculer tous les paramètres orbitaux et le <math>\Delta v</math> dont vous avez besoin pour vos manœuvres. que vous utilisiez un calculateur ou que vous calculiez vos orbites à la main, le mode opératoire est le même que celui explosé ci-dessous. | ||
| − | |||
| − | |||
Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante : | Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante : | ||
| Line 14: | Line 12: | ||
<math>v = \sqrt{\mu\left(\frac{2}{r}-\frac{1}{a}\right)}</math> | <math>v = \sqrt{\mu\left(\frac{2}{r}-\frac{1}{a}\right)}</math> | ||
| − | + | Où | |
| − | <math> | + | * <math>\mu=G \cdot M_{C}</math> est un paramètre gravitationnel du corps orbité (3530,461 km³/s² pour [[Kerbin]]). |
| + | * <math>G</math> est la [http://fr.wikipedia.org/wiki/Constante_gravitationnelle constante gravitationnelle] (<math>6,673 \times 10^{-11} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}</math>). | ||
| + | * <math>M_{C}</math> est la masse du corps orbité. | ||
| + | * <math>r</math> est votre distance au centre du corps que vous orbitez (c'est-à-dire la somme du rayon de la planète et de votre altitude) | ||
| + | * <math>a</math> est le [http://fr.wikipedia.org/wiki/Demi-grand_axe demi-grand axe] de votre orbite (qui est la demi somme des altitudes de vos périastre et apoastre et du diamètre de la planète. | ||
where <math>G</math> is the [[w:gravitational constant|gravitational constant]] <math>6.674 \cdot 10^{-11}\mathrm{\frac{m^3}{kg \cdot s^2}}</math>. Keep in mind that distances to the central body must account not only for altitude but also for the radius (<math>R</math>) of whatever body you are orbiting. The exact values of <math>M</math> and <math>R</math> may be found on their respective pages. | where <math>G</math> is the [[w:gravitational constant|gravitational constant]] <math>6.674 \cdot 10^{-11}\mathrm{\frac{m^3}{kg \cdot s^2}}</math>. Keep in mind that distances to the central body must account not only for altitude but also for the radius (<math>R</math>) of whatever body you are orbiting. The exact values of <math>M</math> and <math>R</math> may be found on their respective pages. | ||
Revision as of 14:09, 23 April 2014
Aller dans l'espace est relativement simple, mais y rester sans retomber au sol ou dériver sans fin dans l'espace est une autre paire de manches. Ce tutoriel vous expliquera comment procéder à une mise en orbite et à y rester, comment circulariser votre orbite ou créer une orbite elliptique et comment diminuer ou augmenter votre orbite.
Contents
Stabiliser une orbite
Lors d'une orbite, votre vaisseau va atteindre une altitude maximale, l''apoastre, et une altitude minimale, le périastre, diamétralement opposés l'un à l'autre. En ces deux points, la vitesse verticale (par rapport à la surface) est nulle, on peut donc aisément calculer notre vitesse orbitale (qui est la même que la vitesse surface). C'est en ces deux endroits qu'il est le plus facile (et le moins coûteux en carburant) de faire des corrections de trajectoire afin de modifier l'orbite. La différence d'altitude entre périastre et apoastre est caractérisée par l'excentricité de l'orbite. Une orbite très circulaire a une excentricité nulle et une orbite très elliptique a une excentricité proche de 1.
Vous trouverez facilement des calculateurs qui vous permettent de calculer tous les paramètres orbitaux et le dont vous avez besoin pour vos manœuvres. que vous utilisiez un calculateur ou que vous calculiez vos orbites à la main, le mode opératoire est le même que celui explosé ci-dessous.
Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante :
Où
- est un paramètre gravitationnel du corps orbité (3530,461 km³/s² pour Kerbin).
- est la constante gravitationnelle ().
- est la masse du corps orbité.
- est votre distance au centre du corps que vous orbitez (c'est-à-dire la somme du rayon de la planète et de votre altitude)
- est le demi-grand axe de votre orbite (qui est la demi somme des altitudes de vos périastre et apoastre et du diamètre de la planète.
where is the gravitational constant . Keep in mind that distances to the central body must account not only for altitude but also for the radius () of whatever body you are orbiting. The exact values of and may be found on their respective pages.
Returning to our case, the higher your orbit, the less gravity you'll feel from Kerbin, so the slower you'll need to go to be in a circular orbit. Determine the proper speed for your altitude at apoapsis or periapsis either by hand, by calculator, or by table. You'll probably want to watch your altimeter as you near one of the critical points, remember the altitude, determine your desired speed, and make the correction on your next pass. If you want to "round out" your orbit from apoapsis, you need to speed up to avoid falling back down to periapsis. Point your craft in the exact direction of travel (use the green circular indicator on the gimbal to line up), and apply thrust until you've gained enough speed. To round out an orbit from periapsis, you need to slow down to avoid climbing back up to apoapsis. Point your craft in the opposite direction of travel (indicated on the gimbal by a green circle with an "X" through it), and apply thrust until you have slowed to the speed indicated by the table. You should then be in an orbit that is very close to circular! Depending on how eccentric your initial orbit was, you may need to make a large correction on your first pass followed by a small correction on a subsequent pass to get very stable.
If you have version 0.11 or better, adding a set of RCS thrusters to your craft can help make minute adjustments to an orbit easier. Version 0.11 also allows you to see the current trajectory (and read periapsis and apoapsis altitudes) by switching to the Map view (M key)
Transfer Orbits
The most efficient way to transfer from a lower circular orbit to a higher circular orbit (or vice-versa) is to use an elliptical transfer orbit, also known as a Hohmann transfer orbit. To transfer, we make the periapsis of the elliptical orbit the same as the radius of the lower orbit, and the apoapsis of the elliptical orbit the same as the radius of the higher orbit. If you are going from low to high, you make a burn in the direction of travel to elongate your orbit. You will climb in altitude as you travel around the planet to the apoapsis of your transfer orbit. Then, make a second burn to round out the new, higher orbit (as described above). To go from high to low, do the opposite: Burn in the opposite direction of travel, then fall down to the periapsis of your transfer orbit, and make a second burn to round out the lower orbit (again in the opposite direction of travel).
Target Speed
The key to transfer orbits is figuring out how much speed to add or subtract to reach a desired new orbital altitude. To do this, use the formula below to determine the target velocity for your initial burn:
In this formula, rl and rh are the radii of the lower and higher orbits, respectively, and ri is the radius of the initial orbit. If you are transferring to a higher orbit, ri will be equal to rl, and v will be faster than your current speed, so burn in the direction of travel to reach v. If you are transferring to a lower orbit, ri will be equal to rh, and v will be slower than your current speed, so burn in the opposite direction to reach v. Remember, v is the target speed for your initial burn that puts you into the elliptical transfer orbit. Once you reach your new orbital altitude, you need to make a second burn to round out your orbit, using the same technique described in the stabilizing your orbit section.
Details of where this formula comes from are in the technical section below. When using this formula, take care to remember that the radius of an orbit is equal to the orbital altitude plus Kerbin's radius (600 000 m).
De-orbiting
The most efficient way to de-orbit from any altitude is to initiate a transfer orbit with a periapsis below 70000 m, the edge of Kerbin's atmosphere. Note that the upper atmosphere is very thin so if you do not want to wait for several orbits of aerobraking, aim for under 35000 m and thicker air. As you approach periapsis, the atmospheric drag will start to slow your craft and eventually it can no longer maintain orbit.
R code snippet for planning Hohmann transfer
hohmann <- function(from_alt,to_alt){
# provides information needed to perform
# a hohmann transfer from a circular ortbit
# at from_alt (km) to a circular orbit at to_alt (km)
mu <- 3530.394 # Gravitational parameter (km^3/s^2)
R <- 600 # Kerbin radius (km)
r1 <- from_alt+R # radius 1 (km)
r2 <- to_alt+R # radius 2 (km)
vc1 <- sqrt(mu/r1) # circular orbit velocity 1 (km/s)
vc2 <- sqrt(mu/r2) # circular orbit velocity 2 (km/s)
a <- (r1+r2)/2 # semi-major axis of transfer orbit (km)
T <- 2*pi*sqrt((a^3)/mu) # period of transfer orbit (s)
dv1 <- (sqrt(r2/a)-1)*vc1 # delta v1 (km/s)
dv2 <- (1-sqrt(r1/a))*vc2 # delta v2 (km/s)
b1 <- list(from=vc1,to=vc1+dv1) # burn one from-to velocities (km/s)
t <- T/2 # time between burns (s)
b2 <- list(from=vc2+dv2,to=vc2) # burn two from-to velocities (km/s)
out <- list(from_alt=from_alt,b1=b1,t=t,b2=b2,to_alt=to_alt)
return(out)}
Example usage
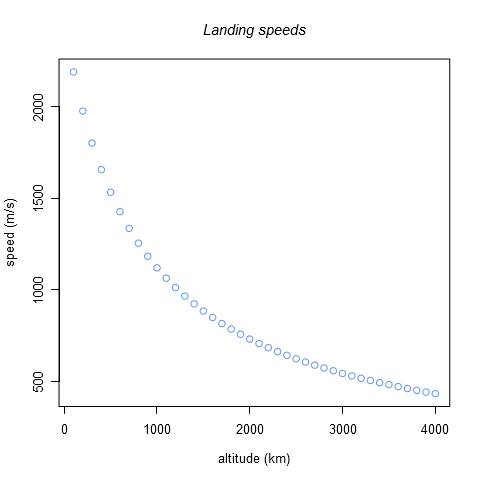
Produce a graph showing the speeds need to transfer from a range of circular orbit altitudes into a landing orbit.
plot(100*1:40,1000*hohmann(100*1:40,34)$b1$to,main="Landing speeds",xlab="altitude (km)",ylab="speed (m/s)")
R project Link [1]
Transfer Orbits
Coming soon!
Orbital Table
Note: The atmosphere previously had a sharp cutoff at 34.5 km, but now extends to approximately 68 km. Below this altitude, your orbit will gradually decay. The decay becomes quite rapid below about 45 km. The orbital parameters below 68 km are provided for reference, but understand that you will not be able to maintain these orbits without regular corrections to counteract the atmospheric drag.
| Altitude (m) | Horizontal Speed (m/s) | Orbital Period (min) |
|---|---|---|
| 40000 | 2348.7 | 28.54 |
| 50000 | 2330.6 | 29.21 |
| 60000 | 2312.8 | 29.88 |
| 70000 | 2295.5 | 30.56 |
| 80000 | 2278.6 | 31.25 |
| 85000 | 2270.3 | 31.60 |
| 90000 | 2262.0 | 31.94 |
| 100000 | 2245.8 | 32.64 |
| 110000 | 2229.9 | 33.34 |
| 120000 | 2214.4 | 34.05 |
| 130000 | 2199.2 | 34.76 |
| 140000 | 2184.3 | 35.48 |
| 150000 | 2169.6 | 36.20 |
| 160000 | 2155.3 | 36.93 |
| 170000 | 2141.3 | 37.66 |
| 180000 | 2127.5 | 38.39 |
| 190000 | 2114.0 | 39.13 |
| 200000 | 2100.7 | 39.88 |
| 210000 | 2087.7 | 40.63 |
| 220000 | 2075.0 | 41.38 |
| 230000 | 2062.4 | 42.14 |
| 240000 | 2050.1 | 42.91 |
| 250000 | 2038.0 | 43.68 |
| 260000 | 2026.1 | 44.45 |
| 270000 | 2014.5 | 45.23 |
| 280000 | 2003.0 | 46.01 |
| 290000 | 1991.7 | 46.79 |
| 300000 | 1980.6 | 47.59 |
| 310000 | 1969.7 | 48.38 |
| 320000 | 1959.0 | 49.18 |
| 330000 | 1948.4 | 49.98 |
| 340000 | 1938.0 | 50.79 |
| 350000 | 1927.8 | 51.61 |
| 360000 | 1917.7 | 52.42 |
| 370000 | 1907.8 | 53.24 |
| 380000 | 1898.0 | 54.07 |
| 390000 | 1888.4 | 54.90 |
| 400000 | 1879.0 | 55.73 |
| 410000 | 1869.6 | 56.57 |
| 420000 | 1860.5 | 57.41 |
| 430000 | 1851.4 | 58.26 |
| 440000 | 1842.5 | 59.11 |
| 450000 | 1833.7 | 59.96 |
| 460000 | 1825.0 | 60.82 |
| 470000 | 1816.5 | 61.69 |
| 480000 | 1808.0 | 62.55 |
| 490000 | 1799.7 | 63.42 |
| 500000 | 1791.5 | 64.30 |
| 510000 | 1783.4 | 65.18 |
| 520000 | 1775.5 | 66.06 |
| 530000 | 1767.6 | 66.95 |
| 540000 | 1759.8 | 67.84 |
| 550000 | 1752.1 | 68.73 |
| 560000 | 1744.6 | 69.63 |
| 570000 | 1737.1 | 70.53 |
| 580000 | 1729.7 | 71.44 |
| 590000 | 1722.4 | 72.35 |
| 600000 | 1715.3 | 73.26 |
| 610000 | 1708.2 | 74.18 |
| 620000 | 1701.1 | 75.10 |
| 630000 | 1694.2 | 76.03 |
| 640000 | 1687.4 | 76.96 |
| 650000 | 1680.6 | 77.89 |
| 660000 | 1673.9 | 78.83 |
| 670000 | 1667.3 | 79.77 |
| 680000 | 1660.8 | 80.71 |
| 690000 | 1654.3 | 81.66 |
| 700000 | 1648.0 | 82.61 |
| 710000 | 1641.7 | 83.56 |
| 720000 | 1635.4 | 84.52 |
| 730000 | 1629.3 | 85.48 |
| 740000 | 1623.2 | 86.45 |
| 750000 | 1617.2 | 87.42 |
| 760000 | 1611.2 | 88.39 |
| 770000 | 1605.3 | 89.37 |
| 780000 | 1599.5 | 90.35 |
| 790000 | 1593.7 | 91.33 |
| 800000 | 1588.0 | 92.32 |
| 810000 | 1582.4 | 93.31 |
| 820000 | 1576.8 | 94.31 |
| 830000 | 1571.3 | 95.30 |
| 840000 | 1565.8 | 96.31 |
| 850000 | 1560.4 | 97.31 |
| 860000 | 1555.0 | 98.32 |
| 870000 | 1549.7 | 99.33 |
| 880000 | 1544.5 | 100.35 |
| 885000 | 1541.9 | 100.86 |
| 890000 | 1539.3 | 101.37 |
| 900000 | 1534.2 | 102.39 |
| 910000 | 1529.1 | 103.41 |
| 920000 | 1524.0 | 104.44 |
| 930000 | 1519.1 | 105.47 |
| 940000 | 1514.1 | 106.51 |
| 950000 | 1509.2 | 107.55 |
| 960000 | 1504.4 | 108.59 |
| 970000 | 1499.6 | 109.64 |
| 980000 | 1494.8 | 110.69 |
| 990000 | 1490.1 | 111.74 |
| 1000000 | 1485.5 | 112.79 |
| 2 868 378 | 1008.910 | 6 hours |
| 8 140 000 | 635.4 | 24 hours |