Difference between revisions of "Tutorial: Basic Orbiting/fr"
(→Vitesse cible) |
m (→Stabiliser une orbite) |
||
| Line 10: | Line 10: | ||
Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante : | Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante : | ||
| − | <math>v = \sqrt{\mu\left(\frac{2}{r}-\frac{1}{a}\right)}</math> | + | :<math>v = \sqrt{\mu\left(\frac{2}{r}-\frac{1}{a}\right)}</math> |
Où | Où | ||
Revision as of 15:02, 23 April 2014
Aller dans l'espace est relativement simple, mais y rester sans retomber au sol ou dériver sans fin dans l'espace est une autre paire de manches. Ce tutoriel vous expliquera comment procéder à une mise en orbite et à y rester, comment circulariser votre orbite ou créer une orbite elliptique et comment diminuer ou augmenter votre orbite.
Contents
Stabiliser une orbite
Lors d'une orbite, votre vaisseau va atteindre une altitude maximale, l''apoastre, et une altitude minimale, le périastre, diamétralement opposés l'un à l'autre. En ces deux points, la vitesse verticale (par rapport à la surface) est nulle, on peut donc aisément calculer notre vitesse orbitale (qui est la même que la vitesse surface). C'est en ces deux endroits qu'il est le plus facile (et le moins coûteux en carburant) de faire des corrections de trajectoire afin de modifier l'orbite. La différence d'altitude entre périastre et apoastre est caractérisée par l'excentricité de l'orbite. Une orbite très circulaire a une excentricité nulle et une orbite très elliptique a une excentricité proche de 1.
Vous trouverez facilement des calculateurs qui vous permettent de calculer tous les paramètres orbitaux et le dont vous avez besoin pour vos manœuvres. que vous utilisiez un calculateur ou que vous calculiez vos orbites à la main, le mode opératoire est le même que celui explosé ci-dessous.
Vous pouvez calculer votre vitesse en tout point de l'orbite par la formule suivante :
Où
- est un paramètre gravitationnel du corps orbité (3530,461 km³/s² pour Kerbin).
- est la constante gravitationnelle ().
- est la masse du corps orbité.
- est votre distance au centre du corps que vous orbitez (c'est-à-dire la somme du rayon de la planète et de votre altitude)
- est le demi-grand axe de votre orbite (qui est la demi-somme des altitudes de vos périastre et apoastre et du diamètre de la planète).
Plus votre altitude est grande, moins vous êtes attirés par Kerbin (le corps orbité), moins votre vitesse doit être élevée pour rester dans une orbite circulaire. Vous pouvez calculer la vitesse appropriée à l'apoastre ou périastre de votre ellipse pour obtenir une orbite circulaire à cette altitude. Connaissant votre vitesse effective à ce point de votre ellipse, vous pouvez calculer de combien vous devez modifier votre vitesse pour obtenir une orbite circulaire. Pour ce faire, vous pouvez utiliser la formule ci-dessus, un calculateur ou une table (voir en fin d'article).
Rappelez-vous qu'en effectuant une manœuvre à une des extrémités de l'orbite, vous entraînerez une changement d'altitude de l'autre extrémité. Par exemple, si vous êtes au périastre (au plus bas, vitesse maximale) et que vous poussez dans la direction pro-grade (pour prendre de la vitesse), l'apoastre va prendre de l'altitude. Au contraire si vous poussez dans la direction rétrograde, votre apoastre va baisser.
En pratique, pour circulariser votre orbite depuis l'apoastre, vous devez prendre de la vitesse. Pointez le nez de la fusée dans la direction pro-grade (cible jaune sans la croix sur la Navball) et allumez les moteurs. Appuyez sur "M" pour passer en mode carte et surveiller l'évolution de votre périastre (qui est en train de monter). Quand apoastre et périastres s'inversent sur votre orbite, coupez les moteurs (touche "X"). Votre orbite est maintenant circulaire. Le moment ou les points s'inversent est très court, entraînez-vous à couper les moteurs au bon moment. Au contraire si vous voulez circulariser votre orbite depuis le périastre, vous devrez perdre de la vitesse. Orientez le vaisseau dans la direction rétrograde (cible jaune avec croix centrale) et effectuez la même opération. Il est périlleux d'effectuer cette manœuvre en un autre point quelconque de l'orbite car cela va modifier à la fois votre apoastre et votre périastre. Par ailleurs, lors de l'injection en orbite de Kerbin, la poussée est très longue et ne peut se faire uniquement à l'apoastre, ce qui entraîne une difficulté à faire une orbite ronde du premier coup. Néanmoins, si vous calculez la vitesse que vous voulez attendre, vous pouvez laisser vos moteurs allumés jusqu'à être à la bonne vitesse et vous garantir un orbite ronde (si vous êtes pile à la bonne altitude, bonne chance).
Orbite de transfert
La manière la plus efficace de passe d'une orbite circulaire à une autre orbite circulaire plus élevée (ou plus basse) est d'utiliser une orbite de transfert elliptique, appelée orbite de Hohmann. Le principe est de modifier notre orbite initiale afin que l'altitude de l'autre extrémité vaille le rayon de l'orbite finale. Ensuite, on patiente jusqu'à atteindre ce point, où on circularise l'orbite. Par exemple pour passer d'une orbite de 100 km à une orbite de 200 km, on effectue une poussé pro-grade et on fait monter notre apoastre à 200 km. Lorsqu'on atteint ce nouvel apoastre, on effectue une autre poussée pro-grade pour faire monter notre périastre à 200 km. Le principe est le même, bien qu'inversé, pour passer à orbite circulaire moins élevée.
Vitesse cible
La clé des orbites de transfert est de connaître la vitesse qu'il faut prendre ou perdre (le ) pour atteindre l'altitude désirée. Pour ce faire, on utilise cette formule, qui découle directement de la formule donnée plus haut.
Où et sont les rayons des orbites initiale et finale.
La différence entre votre vitesse actuelle et la vitesse calculée vous donne directement le (négatif ou positif) à appliquer pour passer sur l'orbite de transfert. Rappelez-vous que vous devrez refaire une poussée à la fin du transfert. Le de cette manœuvre se calcule grâce à la même formule.
Details of where this formula comes from are in the technical section below. When using this formula, take care to remember that the radius of an orbit is equal to the orbital altitude plus Kerbin's radius (600 000 m).
De-orbiting
The most efficient way to de-orbit from any altitude is to initiate a transfer orbit with a periapsis below 70000 m, the edge of Kerbin's atmosphere. Note that the upper atmosphere is very thin so if you do not want to wait for several orbits of aerobraking, aim for under 35000 m and thicker air. As you approach periapsis, the atmospheric drag will start to slow your craft and eventually it can no longer maintain orbit.
R code snippet for planning Hohmann transfer
hohmann <- function(from_alt,to_alt){
# provides information needed to perform
# a hohmann transfer from a circular ortbit
# at from_alt (km) to a circular orbit at to_alt (km)
mu <- 3530.394 # Gravitational parameter (km^3/s^2)
R <- 600 # Kerbin radius (km)
r1 <- from_alt+R # radius 1 (km)
r2 <- to_alt+R # radius 2 (km)
vc1 <- sqrt(mu/r1) # circular orbit velocity 1 (km/s)
vc2 <- sqrt(mu/r2) # circular orbit velocity 2 (km/s)
a <- (r1+r2)/2 # semi-major axis of transfer orbit (km)
T <- 2*pi*sqrt((a^3)/mu) # period of transfer orbit (s)
dv1 <- (sqrt(r2/a)-1)*vc1 # delta v1 (km/s)
dv2 <- (1-sqrt(r1/a))*vc2 # delta v2 (km/s)
b1 <- list(from=vc1,to=vc1+dv1) # burn one from-to velocities (km/s)
t <- T/2 # time between burns (s)
b2 <- list(from=vc2+dv2,to=vc2) # burn two from-to velocities (km/s)
out <- list(from_alt=from_alt,b1=b1,t=t,b2=b2,to_alt=to_alt)
return(out)}
Example usage
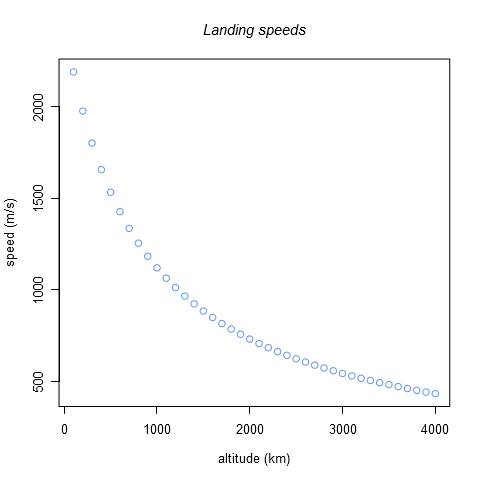
Produce a graph showing the speeds need to transfer from a range of circular orbit altitudes into a landing orbit.
plot(100*1:40,1000*hohmann(100*1:40,34)$b1$to,main="Landing speeds",xlab="altitude (km)",ylab="speed (m/s)")
R project Link [1]
Transfer Orbits
Coming soon!
Orbital Table
Note: The atmosphere previously had a sharp cutoff at 34.5 km, but now extends to approximately 68 km. Below this altitude, your orbit will gradually decay. The decay becomes quite rapid below about 45 km. The orbital parameters below 68 km are provided for reference, but understand that you will not be able to maintain these orbits without regular corrections to counteract the atmospheric drag.
| Altitude (m) | Horizontal Speed (m/s) | Orbital Period (min) |
|---|---|---|
| 40000 | 2348.7 | 28.54 |
| 50000 | 2330.6 | 29.21 |
| 60000 | 2312.8 | 29.88 |
| 70000 | 2295.5 | 30.56 |
| 80000 | 2278.6 | 31.25 |
| 85000 | 2270.3 | 31.60 |
| 90000 | 2262.0 | 31.94 |
| 100000 | 2245.8 | 32.64 |
| 110000 | 2229.9 | 33.34 |
| 120000 | 2214.4 | 34.05 |
| 130000 | 2199.2 | 34.76 |
| 140000 | 2184.3 | 35.48 |
| 150000 | 2169.6 | 36.20 |
| 160000 | 2155.3 | 36.93 |
| 170000 | 2141.3 | 37.66 |
| 180000 | 2127.5 | 38.39 |
| 190000 | 2114.0 | 39.13 |
| 200000 | 2100.7 | 39.88 |
| 210000 | 2087.7 | 40.63 |
| 220000 | 2075.0 | 41.38 |
| 230000 | 2062.4 | 42.14 |
| 240000 | 2050.1 | 42.91 |
| 250000 | 2038.0 | 43.68 |
| 260000 | 2026.1 | 44.45 |
| 270000 | 2014.5 | 45.23 |
| 280000 | 2003.0 | 46.01 |
| 290000 | 1991.7 | 46.79 |
| 300000 | 1980.6 | 47.59 |
| 310000 | 1969.7 | 48.38 |
| 320000 | 1959.0 | 49.18 |
| 330000 | 1948.4 | 49.98 |
| 340000 | 1938.0 | 50.79 |
| 350000 | 1927.8 | 51.61 |
| 360000 | 1917.7 | 52.42 |
| 370000 | 1907.8 | 53.24 |
| 380000 | 1898.0 | 54.07 |
| 390000 | 1888.4 | 54.90 |
| 400000 | 1879.0 | 55.73 |
| 410000 | 1869.6 | 56.57 |
| 420000 | 1860.5 | 57.41 |
| 430000 | 1851.4 | 58.26 |
| 440000 | 1842.5 | 59.11 |
| 450000 | 1833.7 | 59.96 |
| 460000 | 1825.0 | 60.82 |
| 470000 | 1816.5 | 61.69 |
| 480000 | 1808.0 | 62.55 |
| 490000 | 1799.7 | 63.42 |
| 500000 | 1791.5 | 64.30 |
| 510000 | 1783.4 | 65.18 |
| 520000 | 1775.5 | 66.06 |
| 530000 | 1767.6 | 66.95 |
| 540000 | 1759.8 | 67.84 |
| 550000 | 1752.1 | 68.73 |
| 560000 | 1744.6 | 69.63 |
| 570000 | 1737.1 | 70.53 |
| 580000 | 1729.7 | 71.44 |
| 590000 | 1722.4 | 72.35 |
| 600000 | 1715.3 | 73.26 |
| 610000 | 1708.2 | 74.18 |
| 620000 | 1701.1 | 75.10 |
| 630000 | 1694.2 | 76.03 |
| 640000 | 1687.4 | 76.96 |
| 650000 | 1680.6 | 77.89 |
| 660000 | 1673.9 | 78.83 |
| 670000 | 1667.3 | 79.77 |
| 680000 | 1660.8 | 80.71 |
| 690000 | 1654.3 | 81.66 |
| 700000 | 1648.0 | 82.61 |
| 710000 | 1641.7 | 83.56 |
| 720000 | 1635.4 | 84.52 |
| 730000 | 1629.3 | 85.48 |
| 740000 | 1623.2 | 86.45 |
| 750000 | 1617.2 | 87.42 |
| 760000 | 1611.2 | 88.39 |
| 770000 | 1605.3 | 89.37 |
| 780000 | 1599.5 | 90.35 |
| 790000 | 1593.7 | 91.33 |
| 800000 | 1588.0 | 92.32 |
| 810000 | 1582.4 | 93.31 |
| 820000 | 1576.8 | 94.31 |
| 830000 | 1571.3 | 95.30 |
| 840000 | 1565.8 | 96.31 |
| 850000 | 1560.4 | 97.31 |
| 860000 | 1555.0 | 98.32 |
| 870000 | 1549.7 | 99.33 |
| 880000 | 1544.5 | 100.35 |
| 885000 | 1541.9 | 100.86 |
| 890000 | 1539.3 | 101.37 |
| 900000 | 1534.2 | 102.39 |
| 910000 | 1529.1 | 103.41 |
| 920000 | 1524.0 | 104.44 |
| 930000 | 1519.1 | 105.47 |
| 940000 | 1514.1 | 106.51 |
| 950000 | 1509.2 | 107.55 |
| 960000 | 1504.4 | 108.59 |
| 970000 | 1499.6 | 109.64 |
| 980000 | 1494.8 | 110.69 |
| 990000 | 1490.1 | 111.74 |
| 1000000 | 1485.5 | 112.79 |
| 2 868 378 | 1008.910 | 6 hours |
| 8 140 000 | 635.4 | 24 hours |