Terminology/zh-cn
From Kerbal Space Program Wiki
KSP 中使用了大量物理学和轨道飞行的术语,面对这些词语时,非专业人员无疑是会异常困惑,更不要说还有大量的其他科学词汇和缩写了。 本页就是一个相关术语简洁的查询表单,希望能帮助你顺利的走上专业宇航员之路。
Contents
有用的术语
数学与几何学
- 椭圆(elliptical)
- 椭圆形的,一般用于你的轨道的参考。
- 法向量(normal vector)
- 一条与平面垂直的向量。
- 标量(scalar)
- 一个没有方向的数值。标量一般会有测量单位的后缀,表明这个标量的量纲。 比如 3 米每秒(m/s), 3 米(m),3 秒(s) 都是标量:他们有不同的表示速度,长度/距离和时间的单位,但是都没有方向。
- 向量/矢量(vector)
- 一个方向和大小的集合。比如前进方向和速率放在一起就是速度。一个向量如何被表示取决于采用的坐标系,以及多少个维度被使用。 <35°, 12>是一个二维的极坐标向量,而<14, 9, -20>则是一个三维笛卡尔(直角)坐标向量。也有其他的坐标系,但这些是最常用的
- <35°, 12>看起来像是一个12个单位长的箭头,从原点(零点,角度在这里没有意义,因为这是一个没有长度的点)出发,结束在一个与偏离极轴(通常是x轴,逆时针旋转为正角度)35°的点。
- <14, 9, -20>看起来像是一个从原点(<0,0,0>)出发,在一个x坐标为14,y坐标为9,z坐标为20的点终止的箭头。
- 使用直角坐标系的优点是你可以准确的知道向量的终止位置在哪里,但是计算向量的长度则比较麻烦。而在极坐标系中,向量长度十分易得,终止位置却很难得出。
- 速度、加速度、力、动量等物理量都是矢量。
一个三维坐标系需要:
- 一个原点。
- 3个单位向量。这些向量定义了沿着坐标轴的基本量度和坐标轴的方向。
- 3个标量,这可以是角度或坐标,用来描述坐标空间中的位置。
轨道
- 轨道远点(apoapsis)
- 椭圆轨道上,距离轨道中心天体最远的点。
- 轨道近点(periapsis)
- 椭圆轨道上,距离轨道中心天体最近的点。
- 近-* 和 远-* (peri-* and apo-*)
- 谈到轨道,我们通常都用具体的天体名称来指明轨道中心。因此,在这个游戏中,对于环绕 Kerbin 的轨道,我们会用近 Kerbin 点(Perikee 或 Perikerb)、远 Kerbin 点这样的名称(Apokee 或 Apokerb)。
- 升交点(ascending node)
- 以中心天体为参考系,轨道开始向“北”运动的点。“北”向,是参考轨道中心天体的坐标系。
- 降交点(descending node)
- 以中心天体为参考系,轨道开始向南运动的点。
- 离心率(eccentricity)
- 描述轨道几何特征的参数。
- ecc = 0 → 圆形轨道;
- 0 < ecc < 1 → 椭圆轨道;
- ecc = 1 → 抛物线轨道 - 这是一种逃逸轨道;
- ecc > 1 → 双曲线轨道 - 这是另一种逃逸轨道;
- 轨道倾角(inclination)
- 轨道平面与参考平面的夹角。(例如,90° 赤道平面倾角轨道就是所谓的极地轨道。)
- 近Kerbin轨道(low Kerbin orbit, LKO)
- 大多数天体的低轨道都存在于其重力范围内。该轨道高度低,但是稳定(高于大气层)。低轨道通常都是后续飞行的基础,位于上升段和向其他最终的目的地出发之间,在轨道的任意点都可以进行飞船脱离轨道的点火推进。其优点就是抵达低轨道所需要的燃料是最少的。
- 天顶(zenith)
- 地面座标系统中“正上方”的点,也就是火箭在发射场等待发射时指向的点,亦即,“天空中最高的点”。
- 天底(nadir)
- “天顶”的反向点。
- 轨道点(orbital nodes)
- 轨道中的特定点,如近点、远点,以及与其他轨道的交汇点等等。
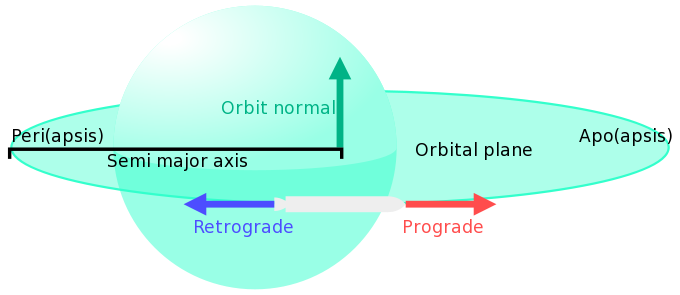
- 轨道法向(orbit normal)
- 轨道平面的正交方向矢量。飞船速度矢量方向与重力矢量方向的矢量和就是轨道法向。其遵照右手规则,飞船在轨道逆时针飞行时,其轨道法向朝“上”,顺时针则朝下。而“上”也就是“北”,或“N+”,“下”也叫做“逆法向”,“南”或者 “N-”。
- 轨道平面(orbital plane)
- 描述轨道环绕飞行平面的虚拟圆盘(通常用于表述轨道倾角)。
- 顺行(prograde)
- 轨道路径的前进方向。由于轨道为椭圆形,因此实际上它的方向是飞船所处轨道位置的切线方向。
- 逆行(retrograde)
- 顺行的反向。
- 参考平面(reference plane)
- 所有飞行器在描述其所处轨道时都需要一个参考平面。对于行星轨道,通常是采用其赤道平面作为参照。类似太阳系的多天体平面为参考时,以黄道平面作为参考平面。在以其他轨道为目标飞行时,应采用目标轨道平面。轨道偏心率和上升点经度(以参考平面为坐标系)即可确定轨道平面。
- 半长轴(semi-major axis)
- 长轴是过焦点与椭圆相交的线长,而半长轴就是椭圆长轴的一半。在 KSP 中,半长轴的计算公式是:
。 轨道运行体的半长轴就是其中心椭圆轨道近点、远点距离的平均值。由于轨道远近点都是相对于轨道中心物体表面的距离,因此需要在公式中加入其半径。半长轴相同的轨道运行周期相同,无论离心率如何。
- 亚轨道(sub-orbital)
- 亚轨道近点位于行星表面之下,亚轨道飞行最终会与该行星发生交会碰撞。
- 推重比(thrust-weight-ratio, TWR)
- 飞船总质量与动力段所有发动机总推力的比值。若TWR>1,飞船可以完成加速和上升。若TWR<1,飞船是无法克服重力和低飞行高度空气阻力的,不过低 TWR 在太空或许可以足够保证飞行器的运动。因为飞船重量(W)与其所处位置的重力加速度(g)成正比,TWR也跟具体位置有关。Mün表面的重力加速度只是Kerbin表面重力加速度的16.6%,因此,TWRKerbin = 1相当于TWRMün = 6。
太空机动
- 大气层制动(Atmospheric Braking)
- → 全文: 空气制动
- 降低轨道近点,使其进入行星的大气层。这种飞行方式可以利用空气阻力降低飞行器的速度。它可以用于再进入(参考下文),也可以应用于轨道的调整,同时节约燃料。
- 点火(Burn)
- 点燃发动机,通常目的是进行轨道调整。
- 圆化调整(Circularizing)
- 这种机动(发动机点火推进)的目的是把轨道的偏心率调整到零,或近似于零。通常是在轨道近/远点打开发动机推力来实现。
- 再进入(Re-entry)
- 就是再进入大气层,并利用空气阻力减速,使飞船进入地面返回轨道。由于需要足够高的速度来避免大气层把飞船“反弹”会太空,这种机动通常都会面临着剧烈的升温压力。在目前的游戏版本中,再进入过程只是个半成品,升温和大气反弹都没有实现。(不过有相关的 MOD)
- 反向点火
- 向飞船前进的反方向点火推进,例如,把发动机喷口转向顺行方向,飞船头部对准逆行方向。这是一个常用的机动,可以在不改变其他轨道参数的情况下降低轨道速度。
物理学
- 加速度(Acceleration)
- 速度的改变率。加速度是矢量,单位为“米/秒2"(m/s2).
- 抛物线轨道(Ballistic trajectory)
- 下落物体的轨道就是抛物线。在火箭飞行中,它就是指飞行器只受重力影响,本身没有任何动力(如推力)的飞行轨道。
- 速度改变量(Delta-v (Δv))
- 飞行器速度的实际改变量或可能改变量。测量单位为米/秒 (m/s)。质量增大会降低 Δv,而增加推力可以提高Δv。这是一个有效计算推进效率的参量。例如,飞行器脱离 Kerbin 大气层并进入稳定轨道所需要的 Δv 大约是 4,000 m/s。
- 能量
- 在轨飞行器的能量是其动能和势能之和。势能的计算公式是 ,动能的计算公式是 ,这里 G 是 万有引力常量,M 是行星的质量,m 是飞行器的质量,R 是距行星中心的距离,而 v 就是飞行器的速度。。总能量大于零,飞行器就进入逃逸轨道。相同半长轴的轨道能量相等。
- 逃逸速度Escape Velocity
- The velocity needed to escape a given planet's gravity well, as given by where G is the gravitational constant, M is the mass of the planet, and r is the radius of the planet.
- g-force (G)
- A measurement of acceleration as expressed in the sea-level force of Earth's gravity with 1 G being about 9.81 m/s². An object at Earth's surface is accelerated at 1 G. The object weighs twice as much when at 2 G acceleration and is weightless when accelerated with 0 G. In orbit and without an engine running all objects experience no acceleration which can be expressed as 0 G.
- Gravity
- The force exerted by all objects with mass. Very weak. Usually only objects with very high mass - ie. planets, moons - have any noticeable effect. Diminishes with the square of distance from the center of mass. So for an object twice as far, experiences only 1/22 = 1/4 of the gravity.
- Gravity Well
- The area around a planet affected by gravity. Actually extends to infinity, but as gravity decreases exponentially with distance, it is only significant within the planet's sphere of influence.
- Orbit
- When an object has sufficient tangential velocity (and is outside the atmosphere, so drag won't slow it down) so that it will keep falling "next" to the planet (never touching ground) its trajectory is called an orbit. Stable orbits are elliptical (a circle is an ellipse with zero eccentricity). If the objects tangential speed exceeds escape velocity it's orbit will be either para- or hyperbolic.
- Specific Impulse (Isp)
- The Isp defines how effective a propulsion system is. The higher the Isp the more powerful is the thrust applied to the rocket with the same fuel mass. The Isp is usually given in seconds but actually the physically correct unit is distance per time which is usually given in meters per second or feet per second. To avoid confusion which unit of speed is used, the physical correct Isp (in distance/time) is divided by the surface gravity of Earth/Kerbin (9.81 m/s²). This results in a value given in seconds. To use this Isp in formulas it must to be converted back into distance per time which requires multiplying with the surface gravity of Earth/Kerbin again. As this value is only used to convert between those two units, the specific impulse doesn't change when the gravity changes.
- As the specific impulse is the ratio of thrust and fuel flow is sometimes given as the unit. This is mathematically another form of because force is the multiplication of mass and acceleration defining . So with the later begin simply only in SI base units.
- Sphere of influence
- The radius around a celestial body where its gravity well is non-neglectable. Commonly known as SoI/SOI.
- Tangential velocity
- The component of your velocity that's perpendicular to your trajectory. Instantaneous velocity - velocity when the time of measurement approaches zero - is always tangential to your trajectory.
- Trajectory
- A trajectory is the path that a moving object follows through space as a function of time.
- Velocity
- Rate of change of your position. Your speed and direction. Velocity is a vector, measured in meters per second (m/s).
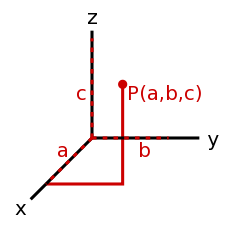
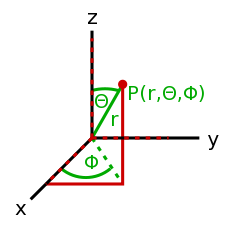







![I_{{sp}}={\frac {T}{{\dot m}}},[I_{{sp}}]={\frac {m}{s}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ff940eef93d9743a07d72ba2bb808e3b0372c36)



