Difference between revisions of "Tutorial:Satellite Coverage"

Latest revision as of 20:23, 2 May 2019

This tutorial is about how to calculate the satellite coverage of a celestial body. This is particularly useful for RemoteTech. Note: When placing multiple satellites in one orbit, it is more important that the semi-major axis is identical for all satellites. With an identical semi-major axis, nil eccentricity, and approximately identical inclination the exact positioning of the apsides is not critical. So long as the eccentricity is as close to nil as possible, variances in apside positioning and inclination will only result in a small oscillation (analemma).

Distance between satellites

Illustrating the calculation

The distance between two satellites (if their angular distance is known) can be calculated with following formula:

l=2\cdot \sin \left({\frac {1}{2}}\alpha \right)\cdot (a+r)

Where $\alpha$ is the angular distance, $a$ the altitude above mean sea level, and $r$ the radius of the orbited body - it is basically an isosceles triangle, where the base length is the distance between the satellites and the legs are from the center of mass of the orbited body to the satellites. For example: two satellites at GSO around Kerbin with a distance of 90° are 4.9 Mm away. This calculation does not work if the altitude of the two satellites is not equal.

Satellite Line-of-Sight communication

Error creating thumbnail: /bin/bash: rsvg-convert: command not found

Six satellites in orbit around a celestial body in a regular polygon shape

Satellites require line-of-sight for communications. Depending on the number of satellites and altitude, it is not always possible to communicate with the other satellites in the same orbit. To mitigate this, either a higher orbit is chosen or more satellites are required. With the following formulas the altitude is linked with the number of satellites to determine at which altitude (and in what quantity) the satellites are required to allow communication.

When all satellites in orbit have the same orbital period, the most efficient way to position them is in the corners of a regular convex polygon. Neighboring satellites should have an angular distance of $\alpha$ . Each satellite is placed on the same circular orbit and their position is a multiple of the following angle:

\alpha ={\frac {\tau }{n}}={\frac {360^{\circ }}{n}}={\frac {2\pi }{n}}

In other words, a satellite is positioned at every multiple of $\alpha$ . The connection between two neighboring satellites and the center of the orbited body form a triangle where the distance from the satellites to the body's center is identical, forming an isoceles triangle. The height of the triangle is the shortest distance between the body's surface and the connection between the satellites. To calculate the height the following formula can be used:

h=\cos \left({\frac {1}{2}}\alpha \right)\cdot (a+r)

Note that $h$ must be greater or equal to $r$ to allow a successful line-of-sight connection:

a\geq \left({\frac {1}{\cos \left({\frac {\tau }{2n}}\right)}}-1\right)\cdot r

To determine how many satellites are needed for a specific altitude (as before, $h$ must be greater than $r$ ):

n\geq {\frac {\tau }{2\cdot \arccos \left({\frac {r}{a+r}}\right)}}

Tau ( $\tau$ ) is equivalent to $2\cdot \pi$ (or 360°). The unit needed depends on which unit is used by cosine and arccosine in the calculations. Note that the number of satellites, $n$ , must be greater than or equal to 3.

Two satellite configuration

When using two satellites it is not possible to position them 180° apart, as the orbited body obstructs the line-of-sight they require. To provide near-100% coverage of an orbital body with only two satellites (at 180° separation) requires a very large $a$ to $r$ ratio and is not optimal. Keep in mind that the two satellites cannot communicate directly (via line-of-sight) and you will need to take measures to ensure connectivity is maintained.

@@ Line 1: / Line 1: @@
-This tutorial is about how to calculate the coverage of a celestial body. This is for example useful for [[Tutorial:RemoteTech|RemoteTech]]. When placing multiple satellites in one orbit, it is more important that the semi-major axis is identical for all satellites. As long as the eccentricity is not very high this is more precise, than trying to make both apsides equal.
+This tutorial is about how to calculate the satellite coverage of a celestial body. This is particularly useful for [[Tutorial:RemoteTech|RemoteTech]]. Note: When placing multiple satellites in one orbit, it is more important that the semi-major axis is identical for all satellites. With an identical semi-major axis, nil eccentricity, and approximately identical inclination the exact positioning of the apsides is not critical. So long as the eccentricity is as close to nil as possible, variances in apside positioning and inclination will only result in a small oscillation ([[w:Analemma|analemma]]).
 == Distance between satellites ==
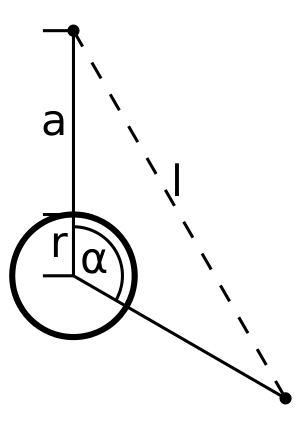
 [[File:Sat-dist.svg|thumb|Illustrating the calculation]]
-To determine the distance between two satellites if their angular distance is known can be calculated with following formula:
+The distance between two satellites (if their angular distance is known) can be calculated with following formula:
 :<math>l = 2\cdot\sin\left(\frac{1}{2}\alpha\right)\cdot(a+r)</math>
-With <math>\alpha</math> being the angular distance, <math>a</math> the altitude above mean sea level and <math>r</math> the radius of the orbited body. It is basically a isosceles triangle, where the base length is the distance between the satellites and the other both sides are from the center of mass of the orbited body to the satellites. For example two satellites at GSO around Kerbin with a distance of 90° are 4.9 Mm away. This calculation don't work, if the altitude of the two satellites isn't equal.
-== General coverage calculations ==
+Where <math>\alpha</math> is the angular distance, <math>a</math> the altitude above mean sea level, and <math>r</math> the radius of the orbited body - it is basically an isosceles triangle, where the base length is the distance between the satellites and the legs are from the center of mass of the orbited body to the satellites. For example: two satellites at GSO around Kerbin with a distance of 90° are 4.9 Mm away. This calculation does not work if the altitude of the two satellites is not equal.
-To determine what altitude is needed to cover a complete body only the radius of the orbited body and the number of used satellites is important.
+== Satellite Line-of-Sight communication ==
+[[File:Sat-polygon.svg|thumb|right|Six satellites in orbit around a celestial body in a regular polygon shape]]
+Satellites require line-of-sight for communications. Depending on the number of satellites and altitude, it is not always possible to communicate with the other satellites in the same orbit. To mitigate this, either a higher orbit is chosen or more satellites are required. With the following formulas the altitude is linked with the number of satellites to determine at which altitude (and in what quantity) the satellites are required to allow communication.
+When all satellites in orbit have the same orbital period, the most efficient way to position them is in the corners of a [[w:Regular polygon|regular]] [[w:Convex and concave polygons|convex]] polygon. Neighboring satellites should have an [[w:Angular distance|angular distance]] of <math>\alpha</math>. Each satellite is placed on the same circular orbit and their position is a multiple of the following angle:
+:<math>\alpha = \frac{\tau}{n} = \frac{360^\circ}{n} = \frac{2\pi}{n}</math>
+In other words, a satellite is positioned at every multiple of <math>\alpha</math>. The connection between two neighboring satellites and the center of the orbited body form a triangle where the distance from the satellites to the body's center is identical, forming an [[w:Triangle#By relative lengths of sides|isoceles triangle]]. The height of the triangle is the shortest distance between the body's surface and the connection between the satellites. To calculate the height the following formula can be used:
+:<math>h = \cos\left(\frac{1}{2}\alpha\right)\cdot(a+r)</math>
-When all satellites in orbit have the same orbital period, the most efficient way to place them is, is in the corners of a [[w:Regular polygon|regular]] [[w:Convex and concave polygons|convex]] polygon. The interior angle of each point is then expressed with following formula:
+Note that <math>h</math> must be greater or equal to <math>r</math> to allow a successful line-of-sight connection:
-:<math>\alpha = \frac{n - 2}{n} \cdot 180^\circ</math>
-Each satellite is placed on the same circle with following distance:
-:<math>\delta = \frac{360^\circ}{n}</math>
-The satellites with an angle of <math>\delta</math> ahead and behind need to be at least <math>\alpha</math> degrees away. The celestial body with a radius of <math>r</math> has at an altitude of <math>a</math> above mean sea level this angular size:
-:<math>\beta = 2 \cdot \sin^{-1}\left(\frac{r}{r+a}\right)</math>
-To have the satellites in sight the celestial body's size <math>\beta</math> has to be lower than <math>\alpha</math>:
-:<math>\frac{n - 2}{n} \cdot 180^\circ = \left(1 - \frac{2}{n}\right) \cdot 180^\circ = \alpha \geq \beta = 2 \cdot \sin^{-1}\left(\frac{r}{r+a}\right)</math>
-The lowest altitude is then, when <math>\alpha = \beta</math>:
-:<math>\begin{align}
-  \left(1 - \frac{2}{n}\right) \cdot 180^\circ & = 2 \cdot \sin^{-1}\left(\frac{r}{r+a}\right)\\
-  \sin\left(\left(1 - \frac{2}{n}\right) \cdot \frac{180^\circ}{2}\right) & = \frac{r}{r+a}\\
-  \frac{1}{\sin\left(\left(1 - \frac{2}{n}\right) \cdot 90^\circ\right)} & = \frac{r+a}{r} = 1+\frac{a}{r}\\
-  \left(\frac{1}{\sin\left(\left(1 - \frac{2}{n}\right) \cdot 90^\circ\right)} - 1\right) \cdot r & = a\\
-\end{align}</math>
-This determines the height needed for ''n'' satellites, but can be reversed to get how many satellites are needed for a specific altitude:
-:<math>\begin{align}
-  \left(1 - \frac{2}{n}\right) \cdot 180^\circ & = 2 \cdot \sin^{-1}\left(\frac{r}{r+a}\right)\\
-- \frac{2}{n} & = \frac{2}{180^\circ} \cdot \sin^{-1}\left(\frac{r}{r+a}\right)\\
-  -\frac{2}{n} & = \frac{1}{90^\circ} \cdot \sin^{-1}\left(\frac{r}{r+a}\right) - 1\\
-  \frac{1}{n} & = -\frac{\frac{1}{90^\circ} \cdot \sin^{-1}\left(\frac{r}{r+a}\right) - 1}{2}\\
-  n & = -\frac{2}{\frac{1}{90^\circ} \cdot \sin^{-1}\left(\frac{r}{r+a}\right) - 1}\\
-\end{align}</math>
-These calculations work only with at least three satellites.
+:<math>a \geq \left(\frac{1}{\cos\left(\frac{\tau}{2n}\right)}-1\right)\cdot r</math>
+To determine how many satellites are needed for a specific altitude (as before, <math>h</math> must be greater than <math>r</math>):
+:<math>n \geq \frac{\tau}{2\cdot\arccos\left(\frac{r}{a+r}\right)}</math>
+Tau (<math>\tau</math>) is equivalent to <math>2\cdot\pi</math> (or 360°). The unit needed depends on which unit is used by cosine and [[w:Inverse trigonometric functions|arccosine]] in the calculations. Note that the number of satellites, <math>n</math>, must be greater than or equal to 3.
 == Two satellite configuration ==
-When using two satellites it is not possible to place them 180° apart, as they have no connection to each other than. So only two satellites can cover the complete celestial body. But when making the distance between both satellites as high as possible to 180°, it is possible to cover most of the body.
-[[Category:Tutorials]]
+When using two satellites it is not possible to position them 180° apart, as the orbited body obstructs the line-of-sight they require. To provide near-100% coverage of an orbital body with only two satellites (at 180° separation) requires a very large <math>a</math> to <math>r</math> ratio and is not optimal. Keep in mind that the two satellites cannot communicate directly (via line-of-sight) and you will need to take measures to ensure connectivity is maintained.
+[[Category:Tutorials|Satellite Coverage]]

Difference between revisions of "Tutorial:Satellite Coverage"

Latest revision as of 20:23, 2 May 2019

Distance between satellites

Satellite Line-of-Sight communication

Two satellite configuration

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation

KSP links

Quick access

Languages

Data templates

Tools