Difference between revisions of "Terminology/th"
m |
|||
| (32 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | KSP มีคำศัพท์หลายคำที่เกี่ยวข้องกับ วงโคจรและฟิสิกส์ที่ใช้บ่อยและอาจสับสนกับคำศัพท์ธรรมดา และยังมีคำศัพท์ทางวิทยาศาสตร์และตัวย่อที่มักจะใช้ในอธิบายภายในเกมส์ | |
| − | + | หน้านี้ได้ถูกออกแบบมาให้กระชับในการค้นหาคำศัพท์ต่างที่จะช่วยคุณเรียนรู้เพื่อจะเป็นนักบินอวกาศมากความสามารถในอนาคต | |
| − | == | + | == คณิตศาสตร์== |
| − | <div style="float:right;">[[File:cartesian.svg|thumb|upright|left| | + | <div style="float:right;">[[File:cartesian.svg|thumb|upright|left|ระบบพิกัดคาร์ทีเซียน - ใช้พิกัดฉาก]][[File:polar.svg|thumb|upright|ระบบพิกัดเชิงขั้ว - ใช้เฉพาะมุมและความยาว]]</div> |
| − | ;Elliptical | + | ;วงรี (Elliptical) |
| − | : | + | :รูปทรงวงรี ส่วนมากใช้บอกถึงลักษณะวิถีวงโคจรที่เป็นรูปวงรี |
| − | ;Hyperbolic | + | ;ไฮเปอร์โบลา (Hyperbolic) |
| − | : | + | :เส้นวิถีโค้งปลายเปิด ปกติจะเป็นการแสดงวิถีออกจากวงโคจร(escape trajectories) |
| − | ;Normal vector | + | ;เว็กเตอร์ตั้งฉาก (Normal vector) |
| − | : | + | :เวกเตอร์ที่ตั้งฉากกับยานอวกาศของคุณ |
| − | ;Scalar | + | ;สเกลาร์ (Scalar) |
| − | : | + | :เป็นหน่วยที่มีขนาด แต่ไม่มีทิศทาง, ซึ่งจำนวนสเกลาร์มักจะใช้ในหน่วยที่วัดต่างๆ เช่น 3 m/s (เมตร/วินาที), 3 m(เมตร),3 s(วินาที) เป็นต้น ซึ่งหน่วยต่างๆดังกล่าว จะบอกถึงค่าของความเร็ว ความยาว หรือเวลา แต่จะไม่บอกทิศทางของหน่วยนั้นๆ |
| − | ;Vector | + | ;เว็กเตอร์ (Vector) |
| − | : | + | :เป็นหน่วยที่่มีทั้งขนาดและทิศทาง เช่น ทิศทางการบิน(Heading) และอัตราเร็ว(Speed) และจะได้ ความเร็ว(Velocity). เว็กเตอร์จะถูกเขียนได้หลายแบบซึ่งขึ้นอยู่กับระบบพิกัด(Coordinate system) เช่น <35°, 12> คือเว็กเตอร์เชิงขั้วสองมิติ หรือ <14, 9, -20> เวกเตอร์คาร์ทีเซียนสามมิติ นอกจากนี้ยังมีระบบพิกัดอีกหลายแบบ แต่สองแบบนี้มักจะใช้บ่อยที่สุด |
| + | :<35°, 12> หน้าตาคล้ายกับลูกศรที่ยาว 12 หน่วย และเริ่มจากจุดเริ่มต้นทำมุม 35° กับแกนฐานของจุดเริ่มต้น (โดยปกติจะวัดทำมุมกับแกน x และวัดทวนเข็มนาฬิกา) | ||
| − | :< | + | :<14, 9, -20> หน้าตาคล้ายกับลูกศรที่มีจุดเริ่มต้น (<0,0,0>) และจุดสุดท้ายมีพิกัดที่แกน x ที่ 14 หน่วย แกน y ที่ 9 หน่วย และแกน z ที่ -20 |
| − | : | + | :ข้อดีของการใช้เว็กเตอร์แบบต่างๆ เว็กเตอร์คาร์ทีเซียนจะสามารถบอกจตำแหน่งสุดท้ายได้ แต่จะยากในหาความยาวของเว็กเตอร์ แต่สำหรับเว็กเตอร์เชิงขั้วจะง่ายมากในการหาความยาวของเว็กเตอร์แต่จะยากในการหาตำแหน่งสุดท้ายของเว็กเตอร์ |
| − | : | + | :เว็กเตอร์ต่างๆที่ใช้ในทางฟิสิกส์: '''ความเร็ว (velocity)''', '''ความเร่ง (acceleration)''', '''แรง (force)''' |
| − | : | + | ระนาบสามมิติ ต้องการ: |
| + | * จุดอ้างอิง ส่วนมากคือจุดเริ่มต้น (<0,0,0>) | ||
| + | * 3 เว็กเตอร์ฐาน จะเป็นตัวกำหนดหน่วยฐานในการวัดในแนวแกนต่างๆ (แกน x,y,z) | ||
| + | * การผสมของสเกลาร์ 3 ตัว อาจจะเป็นได้ทั้ง มุม หรือพิกัด ที่จะสามารถแสดง ตำแหน่งในระนาบได้ | ||
| − | + | == ศัพท์เกี่ยวกับวงโคจร == | |
| − | + | [[File:Orbit.svg|thumb|upright=2.25|ภาพแสดงถึงตัวแปลทั่วไปของวงโคจร]] | |
| − | + | ;<span id="ap">จุดไกลที่สุด (Apoapsis)</span> | |
| − | + | ;<span id="pe">จุดใกล้ที่สุด (Periapsis)</span> | |
| − | |||
| − | == | ||
| − | [[File:Orbit.svg|thumb|upright=2.25| | ||
| − | ;<span id="ap">Apoapsis</span> | ||
| − | ;<span id="pe">Periapsis</span> | ||
;Apsis | ;Apsis | ||
{{See also|Orbit|section=Apoapsis and periapsis}} | {{See also|Orbit|section=Apoapsis and periapsis}} | ||
| − | : | + | :ทุกวงโคจรที่เป็นวงรี จะมีสองด้านเสมอ(2 apsides). '''periapsis''' (<tt>q</tt>) คือจุดที่ใกล้กับดาวมากที่สุดในวงโคจร (จุดต่ำที่สุดในวงโคนจร) และ '''apoapsis''' (<tt>Q</tt>) จุดที่อยู่ตรงข้างในวงโคจร และมีระยะใกลที่สุดจากดาวในวงโคจร (จุดสูงสุดในวงโคจร). '''apsides''' ปกติจะเป็นค่าความสูงจากพื้นผิวของดาว แต่การคำนวนต่างๆจะต้องคิดจากจุดศูนย์กลางของดาวเสมอ เพราะฉนั้นเราจำเป็นต้องบวกรัศมีของดาวเข้าไปในการคำนวนเสมอ |
;<span id="appe">Peri-* and Apo-*</span> | ;<span id="appe">Peri-* and Apo-*</span> | ||
| − | : | + | :ในการพูดเกี่ยวกับวงโคจร, บางครั้งคำว่า "periapsis" และ"apoapsis" อาจจะถูกดัดแปลงเพื่อเรียกเฉพาะกับดาวหรือดวงจันทร์ที่มีวงโคจรอยู่รอบๆ ตัวอย่างเช่น -kee และ -kerb มักจะใช้ในการอ้างถึงวงโคจรรอบๆ Kerbin และทำให้เกิดคำว่า Perikee/Perikerb and Apokee/Apokerb เป็นต้น |
| − | ;<span id="an">Ascending node</span> | + | ;<span id="an">จุดตัดขึ้น (Ascending node)</span> |
| − | : | + | :จุดตัด([[#on|orbital node]]) ที่ทำให้การเคลื่อนที่มุ่งไปทางทิศเหนือ (เหนือในที่นี้คือ ทิศทางที่ตั้งฉากกับวงโคจร (Orbital Normal)) |
| − | ;<span id="dn">Descending node</span> | + | ;<span id="dn">จุดตัดลง (Descending node)</span> |
| − | : | + | :จุดตัด([[#on|orbital node]]) ที่ทำให้การเคลื่อนที่มุ่งไปทางทิศใต้ |
| − | ;<span id="ecc">Eccentricity</span> | + | ;<span id="ecc">ความรี (Eccentricity)</span> |
{{See also|Orbit|section=Eccentricity}} | {{See also|Orbit|section=Eccentricity}} | ||
<math style="float:right;padding:0.5em;">\text{ecc} = 1 - \frac{2}{\frac{Ap}{Pe}+1}</math> | <math style="float:right;padding:0.5em;">\text{ecc} = 1 - \frac{2}{\frac{Ap}{Pe}+1}</math> | ||
| − | : | + | :หน่วยสเกล่าที่อธิบายถึงความไม่กลมของวงโคจร ดังนี้ |
| − | :* ecc = 0 → | + | :* ecc = 0 → วงโคจรแบบกลม. |
| − | :* 0 < ecc < 1 → | + | :* 0 < ecc < 1 → วงโคจรแบบวงรี. |
| − | :* ecc = 1 → | + | :* ecc = 1 → วงโคจรแบบพาราโบลา - วิถีออกจากวงโคจร |
| − | :* ecc > 1 → | + | :* ecc > 1 → วงโคจรแบบไฮเปอร์โบลา - วิถีออกจากวงโคจร |
| − | ;<span id="inc">Inclination</span> | + | ;<span id="inc">ความเอียง (Inclination)</span> |
{{See also|Orbit|section=Inclination}} | {{See also|Orbit|section=Inclination}} | ||
| − | + | มุมที่ทำระหว่างระนาบวงโคจรกับระนาบอ้างอิง (เช่น วงโคจรที่มีความเอียง 90° กับระนาบเส้นศูนย์สูตร จะเรียกว่า โพลา (polar)) | |
| − | ;<span id="lo">Low orbit</span> | + | ;<span id="lo">วงโคจรระดับต่ำ (Low orbit)</span> |
| − | : | + | :วงโคจรที่สูงพอที่จะไม่ถูกรบกวนจากสภาวะแวดล้อมของดาว เช่น แรงเสียดทานจากชั้นบรรยากาศ เป็นต้น วงโคจรระดับต่ำมักจะใช้เป็นบันไดพักขั้นแรกหลังจากที่เราทำการเพิ่มความสูงและก่อนที่จะทำการจุดเครื่องยนต์เพื่อจะไปยังดวงดาว หรือวัตถุอื่นๆในอวกาศ. ทั้งยังสามารถทำการจุดเครื่องยนต์ไปได้ในทุกทิศทาง และต้องการเชื้อเพลิงไม่มากในการมาถึงจากพื้นผิวของดาว วงโคจรระดับต่ำสำหรับ [[Kerbin]] นั้นอยู่ระหว่างประมาณ 80 -100 กิโลเมตร สำหรับดาวที่ไม่มีชั้นบรรยากาศสามารถทำวงโคจรในทางทฤษฎี ได้ทุกความสูงเหนือพื้นผิว แต่การทำวงโคจรที่ต่ำกว่าระดับ 10 กิโลเมตรนั้นมีความเสี่ยงที่จะชนกับภูเขาหรือพื้นผิวที่มีความสูงมาก ส่วน [[time warp]] จะมีข้อจำกัดในการบินในวงโคจรระดับต่ำ |
| − | ;<span id="on">Orbital node</span> ''(astronomical definition)'' | + | |
| − | : | + | ;<span id="on">จุดตัด (Orbital node)</span> ''ความหมายในทางอวกาศ(astronomical definition)'' |
| − | ;<span id="node">Orbital nodes</span> ''(as in game)'' | + | :จุดที่วงโคจรตัดผ่านระนาบอ้างอิง ณ จุดตัดขึ้น [[#an|จุดตัดขึ้น (ascending node)]] ยานจะเคลื่อนผ่านระนาบอ้างอิงในทิศตั้งฉากกับวงโคจร(Orbital Normal) โดยปกติแล้วจุดขึ้นมักจะชี้ไปทางทิศเหนือและจุดลงจะชี้ไปยังทิศใต้ |
| − | : | + | ;<span id="node">จุดตัด (Orbital nodes)</span> ''ภายในเกมส์(as in game)'' |
| − | ;<span id="orbnorm">Orbit normal</span> | + | :จุดอ้างอิงจำเพาะทุกจุดที่อยู่บนวงโคจรเช่น [[#ap|จุดไกลสุด (Apoapsis)]], [[#pe|จุดใกล้สุด (Periapsis)]],จุดตัดกับวงโคจรอื่น เป็นต้น |
| − | : | + | ;<span id="orbnorm">ทิศตั้งฉากกับวงโคจร (Orbit normal)</span> |
| − | ;<span id="orbplane">Orbital plane</span> | + | :เว็กเตอร์ตั้งฉากกับระนาบวงโคจร โดยปกติจะเกิดจากผลคูณไขว้ของความเร็วยานกับแรงโน้มท่วง และทำให้เว็กเตอร์สอดคล้องกับกฏมีอขวา จากมุมมองที่ยานทำวงโคจรทวนเข็มนาฬิกาเว็กเตอร์นี้จะชี้ขึ้น ในทางตรงกันข้ามถ้ายานทำวงโคจรตามเข็มนาฬิกาเว็กเตอร์จะชี้ลง โดยปกติแล้ว "ขึ้น" มักจะถูกเรียกว่า "ทิศเหนือ(North)" หรือ "N+" ในส่วนของ "ลง" มักจะเรียกว่า "Anti-Normal","ใต้ (South)" หรือ "N-" |
| − | : | + | ;<span id="orbplane">ระนาบวงโคจร (Orbital plane)</span> |
| − | ;<span id=" | + | :แผ่นกลมในจินตนาการโดยเป็นวิถีของวงโคจรรอบดาว (โดยปกติใช้ใช้อธิบายความเอียง) |
| − | : | + | ;<span id="orb speed">อัตราเร็ววงโคจร (Orbital speed)</span> |
| − | ;<span id="prograde">Prograde</span> | + | :อัตราเร็วของการโคจรของดาวใดๆนั้น คือความเร็วที่โคจรรอบศูนย์กลางแรงโน้มท่วงของระบบ, โดยปกติจะเป็นดาวที่มีมวลมหาศาล และยังสามารถหมายถึงความเร็วในการทำวงโคจร เช่น ค่าเฉลี่ยความเร็วที่สามารถทำให้วงโคจรสมบูลย์ หรือความเร็วในจุดใดจุดหนึ่งบนวงโคจร |
| − | : | + | ;<span id="prograde">ทิศเดินหน้า Prograde</span> |
| − | ;<span id="retrograde"> | + | :ทิศทางที่ยานเดินทางตามวิถีของวงโคจร เมื่อวงโคจรเป็นวงรี มันมักจะเป็นเส้นสัมผัส(Tangent)กับวิถีวงโคจร ณจุดที่ยานอยู่ |
| − | : | + | ;<span id="retrograde">ทิศถอยหลังRetrograde</span> |
| − | ;<span id="refplane">Reference plane</span> | + | :ส่วนกลับของทิศเดินหน้า จะย้อนกลับตามวิถีวงโคจร |
| − | : | + | ;<span id="refplane">ระนาบอ้างอิง (Reference plane)</span> |
| − | ;<span id="sma">Semi-major axis</span> | + | :ทุกระนาบที่ใช้เป็นระนาบอ้างอิงเพื่อจะอธิบายวงโคจรปัจจุบันของคุณ สำหรับวงโคจรรอบดาวเคราะห์ มักจะใช้ระนาบเส้นศูนย์สูตร(Equatorial plane)เป็นระนาบอ้างอิง หากมีดาวหลายๆในระบบสุริยะระนาบวงรีก็สามารถใช้ได้ สำหรับการตัดกันของวงโคจรของดาว วงโคจรของดาวที่กำลังจะตัดกันอาจจะใช้เป็นระนาบอ้างอิงได้ ระนาบวงโคจรสามารถให้ข้อมูลเกี่ยวกับ ความเอียง และ เส้นแวงของจุดขึ้น ที่สัมพันธ์กับระนาบอ้างอิงได้ |
| + | ;<span id="sma">ระยะกึ่งแกนเอก (Semi-major axis)</span> | ||
<math class="float-right">\text{a} = \text{R} + \frac{Q+q}{2}</math> | <math class="float-right">\text{a} = \text{R} + \frac{Q+q}{2}</math> | ||
{{See also|Orbit|section=Semi-major axis}} | {{See also|Orbit|section=Semi-major axis}} | ||
| − | : | + | :แกนเอกคือแกนที่ยาวที่สุดของวงรี และระยะกึ่งแกนเอก(<tt>a</tt>)คือระยะครึ่งหนึ่งของแกนเอก ซึ่งจะเป็นค่าเฉลี่ยของจุดสูงสุด(Apoapsis) (<tt>Q</tt>) และจุดต่ำสุด (Periapsis)(<tt>q</tt>) ที่คำนวนจากศูนย์กลางของดาว ซึ่งทั้งสองสัมพันธ์กับพื้นผิวของดาว โดยที่รัศมีของดาว (<tt>R</tt>) จำเป็นต้องบวกเข้าไปด้วย และทุกๆวงโคจรที่มีระยะกึ่งแกนเอกเท่ากันจะมีคาบเวลาวงโคจรเท่ากัน โดยไม่คำนึงถึงความรีของวงโคจร |
| − | ;<span id="sidereal period">Sidereal period</span> | + | ;<span id="sidereal period">คาบดาราคติ (Sidereal period)</span> |
| − | : | + | :คาบดาราคิติคือคาบเวลาขณะหนึ่งที่วัตถุทำวงโคจรครบรอบ เมื่อเทียบกับดวงดาว ซึ่งเป็นคาบวงโคจรที่ใช้แรงเฉื่อยเป็นกรอบการอ้างอิง(ไม่ใช้การหมุน) |
| − | ;<span id="suborb">Sub-orbital</span> | + | ;<span id="suborb">วงโคจรย่อย (Sub-orbital)</span> |
| − | : | + | :การอธิบายวงโคจรที่จุดต่ำสุด(Periapsis)นั้นอยู่ใต้พิ้นผิวของดาวนั้นๆ ถ้าเรายังเดินทางตามวิถีของวงโคจรย่อยเราก็จะกลับมาชนกับดาวที่เราทำวงโคจรอยู่ |
| − | ;<span id="synodic period">Synodic period</span> | + | ;<span id="synodic period">คาบซินโนดิค (Synodic period)</span> |
| − | : | + | :คาบซินโนดิคคือคาบเวลาขณะหนึ่งที่ทำให้วัตถุนั้นกลับมาอยู่ในตำแหน่งเดิมที่มีความสัมพันธ์ตั้งแต่ สองขึ้นไป ตัวอย่างเช่น เมื่อ [[Mun|Mun]] มีความสัมพันธ์กับ [[Kerbol]] และหาสังเกตการจาก [[Kerbin]] ในแต่ละคาบเราจะกลับมาอยู่เฟสด้านสว่างเหมือนกัน คาบซินโนดิคคือเวลาที่ผ่านไประหว่างวัตถุสองวัตถุ และมีสันธานร่วมกันอย่างสมบูลย์ที่ [[Kerbol]] - [[Kerbin]] เรียงตัวกันในแนวเส้นตรงตามลำดับ ซึ่ง คาบซินโนดิคจะต่างจากคาบดาราคติตรงที่การโคจรของ Kerbin รอบๆ Kerbol |
| − | == Ship Orientation == | + | == ทิศทางของยาน (Ship Orientation) == |
| + | ทิศทางของยานปกติจะต้องมีความสัมพันธ์กับวัตถุใดวัตถุหนึ่ง โดยปกติจะอ้างอิงกับ ห้องนักบิน | ||
The ship orientation is always relative to a specific object. The terms are usually defined relative to the cockpit. | The ship orientation is always relative to a specific object. The terms are usually defined relative to the cockpit. | ||
| − | ;Zenith | + | ;จุดสูงสุด (Zenith) |
| − | : | + | :ด้านบนของบาน ปกติจะอยู่ห่างจากดาวที่ทำวงโคจรอยู่ และอยู่ตรงข้ามกับจุดต่ำสุด (nadir) |
| − | ;Nadir | + | ;จุดต่ำสุด (Nadir) |
| − | : | + | :ด้านล่างของยานซึ่งปกติจะหันไปทางดาวที่ทำวงโคจรอยู่ และอยู่ตรงข้ามกับจุดสูงสุด (Zenith) |
| − | ;Port(side) | + | ;พอร์ท (Port(side)) |
| − | : | + | :ด้านซ้ายของตัวยาน ตรงข้ามกัน สตาร์บอร์ด(Starboard) |
| − | ;Starboard | + | ;สตาร์บอร์ด (Starboard) |
| − | : | + | :ด้านขวาของตัวยาน ตรงกันข้ามกันพอร์ท(Portside) |
| − | ;Front | + | ;ด้านหน้า (Front) |
| − | : | + | :ด้านหน้าของยานปกติจะอยู่ทางจมูกยานหรือเว็กเตอร์ทิศเดินหน้า(Prograde) |
| − | ;Aft | + | ;อัฟท์ (Aft)* |
| − | : | + | :ด้านหลังโดยปกติจะเป็นที่อยู่ของเครื่องยนต์หลัก และหันหน้าไปทาง ทิศย้อนกลับ(Retrograde) |
| − | == Space Maneuvers == | + | ==การเคลื่อนในอวกาศ (Space Maneuvers) == |
| − | ;Atmospheric braking | + | ;เบรคด้วยชั้นบรรยากาศ (Atmospheric braking) |
{{Main article|Aerobraking}} | {{Main article|Aerobraking}} | ||
| − | :Lowering the periapsis so it is inside a planetary atmosphere. This will lead to the vessel being slowed by atmospheric drag. Can lead to atmospheric entry, but also is used to reduce the necessary burn time for significant orbit alterations. | + | :ลดระดับของจุดต่ำสุด(Periapsis) ให้อยู่ในระยะของชั้นบรรยากาศของดาว การกระทำเช่นนี้จะทำให้ยานสามารถลดความเร็วจากแรงเสียดทานในชั้นบรรยากาศได้ และยังสามารถนำไปสู่การกับเข้าชั้นบรรยากาศได้อีกด้วยซึ่งช่วยลดการใช้เชื้อเพลิงในการเปลี่ยนรูปแบบวงโคจร |
| − | ;Lithobraking | + | Lowering the periapsis so it is inside a planetary atmosphere. This will lead to the vessel being slowed by atmospheric drag. Can lead to atmospheric entry, but also is used to reduce the necessary burn time for significant orbit alterations. |
| + | ;ลิโทรเบรคกิ้ง (Lithobraking) | ||
{{See also||{{Wikipedia|Lithobraking}}}} | {{See also||{{Wikipedia|Lithobraking}}}} | ||
| − | : | + | :แทนที่เราจะใช้อากาศในการช่วยเบรค แต่นี้เราใช้ "พื้น" แทนอากาศ ปกติเราจะใช้คำเพื่อล้อเลียนการลงแบบตกกระแทกพื้น ซึ่งไม่ได้อยู่ในแผนที่วางไว้ ซึ่งคำนี้เกิดจากการผวนมาจากคำว่า "Aerobreaking" โดยที่เปลี่ยนจาก "Aero" มาเป็น "lithos" ซึ่งแปลว่า หิน ในภาษากรีก |
| − | ;<span id="atmospheric entry">Atmospheric entry</span> | + | ;<span id="atmospheric entry">เข้าสู่ชั้นบรรยากาศ (Atmospheric entry)</span> |
{{Main article|Atmospheric entry}} | {{Main article|Atmospheric entry}} | ||
| − | : | + | :การเข้าสู่ชั้นบรรยากาศและใช้แรงเสียดทานในการลดความเร็วของยาน เพื่อให้เข้าสู่วิถีลงพื้น. ในโลกความจริงของวิทยาศาสตร์ นี้จะสร้างความเครียดที่เกิดจากความร้อนบนวัตถุ ฉนั้นยานจะต้องมีความเร็วที่เพียงพอที่จะไม่เด้งกลับไปยังอวกาศอีกครั้ง ปัจจุบันการเข้าสู่บรรยากาศในเกมส์ยังพัฒนาเพียงส่วนหนึ่งมีเพียงผลกระทบบางอย่าง แต่ไม่รวมถึงความร้อนและการเด้งออกสู่อวกาศยังไม่ถูกพัฒนา แต่ก็สามารถใช้ ส่วนเสริมของเกมส์ที่สามารถทำให้ชิ้นส่วนยานร้อนเกินไปได้ ([[Overheating|overheat]]) และปกติจะเรียกว่า รีเอ็นทรี่(re-entry/reentry) |
| − | ;Burn | + | ;เบิร์น (Burn) |
| − | : | + | :การจุดเครื่องยนต์ ,ใช้ในการเปลี่ยนวิถีการบิน |
| − | ;Circularizing | + | ;เซอร์เคิลไลซิงก์(Circularizing) |
| + | การลดความรี([[#ecc|eccentricity]])ของวงโคจรให้เข้าใกล้ 0 มากที่สุด ส่วนมาจะเบิร์นใกล้ๆ จุด apsis | ||
:Reducing an orbit's [[#ecc|eccentricity]] to 0 or close to it. This is usually achieved by a burn close to an apsis. | :Reducing an orbit's [[#ecc|eccentricity]] to 0 or close to it. This is usually achieved by a burn close to an apsis. | ||
| − | ;Maneuver node | + | ;จุดเปลี่ยนทิศทาง (Maneuver node) |
{{Main article|Maneuver node}} | {{Main article|Maneuver node}} | ||
| − | : | + | :เป็นการวางแผนการเปลี่ยนเส้นทางบนแผนที่ จึงต้องใช้ [[#burn|burn]] ในการทำ. |
| − | ;Radial-in burn | + | ;เบิร์นเข้าสู่ศูนย์กลาง(Radial-in burn) |
| − | : | + | :การเบิร์นเข้าสู่ศูนย์กลางของดาวเคราะห์ และจะทำการหมุนวงโคจร ทวนเข็มนาฬิกาจนกว่าจุดต่ำสุด(Periapsis)จะผ่านจุดศูนย์ถ่วงของดาวเคราะห์ และตรงข้ากับเบิร์นออกจากศูนย์กลาง |
| − | ;Radial-out burn | + | ;เบิร์นออกจากศูนย์กลาง(Radial-out burn) |
| − | : | + | :การเบิร์นออกจากศูนย์กลางดาวเคราะห์โดยตรง และจะทำให้การหมุนวงโคจร หมนตามเข็มนาฬิกาจนจุดต่ำสุด(Periapsis)จะผ่านจุดศูนย์ถ่วงของดาวเคราะห์ |
;Radial burn | ;Radial burn | ||
{{See also|Maneuver node|Maneuver node}} | {{See also|Maneuver node|Maneuver node}} | ||
;Re-entry | ;Re-entry | ||
{{See also|#atmospheric entry|Atmospheric entry}} | {{See also|#atmospheric entry|Atmospheric entry}} | ||
| − | ;Retroburn | + | ;รีโทรเบิร์น(Retroburn) |
| − | : | + | :การเบิร์นที่ทำให้เกิดการ "ถอยหลัง", เช่น การทำให้เครื่องยนหันไปทางด้านหน้า(Prograde) และด้านหน้าหักไปทางด้านหลัง(Retrograde) โดยปกติจะใช้ท่าการบินนี้สำหรับการลดระดับจุดต่ำสุด([[#periapsis|periapsis]]) และจุดสูงสุด([[#apoapsis|apoapsis]]) |
| − | == Physics == | + | == ฟิสิกค์(Physics) == |
| − | ;Acceleration | + | ;ความเร่ง(Acceleration) |
| − | : | + | :อัตราการเปลี่ยนแปลงของความเร็ว(Velocity), ความเร่งเป็นเว็คเตอร์ และมีหนวยเป็น "m/s<sup>2</sup>" |
| − | ;Ballistic trajectory | + | ;วิถีกระสุน(Ballistic trajectory) |
| − | : | + | :การร่วงหล่นของวัตถุจะมีวิธีที่เป็นวิถีแบบกระสุน ในเรื่องที่เกี่ยวกับจรวดจะแสดงถึงวัตถุที่มีปฏิสัมพันธ์กับแรงดึงดูดเท่านั้นและไม่มีแรงอื่นมากระทำไม่เว้นแม้แต่แรงขับจรวด |
| − | ;Delta-v (Δv) | + | ;เดลต้าวี(Delta-v (Δv)) |
| − | : | + | :การเปลี่ยนของความเร็วที่กำเนิดมาจากยานอวกาศ และมีหน่วยในการวัดเป็นเมตรต่อวินาที(m/s) มวลที่มากขี้นจะลดเดลต้าวีให้ลดลง แต่หากมีแรงขับมากขึ้นจะสามารถเพิ่มเดลต้าวีได้ ค่านี้เป็นค่าที่สำคัญในการคำนวนความคุ้มค้าและประสิทธิภาพของจรวด ตัวอย่างเช่น การยิงยานต้องการเดลต้าวีประมาณ 4500 m/s ในการออกจากชั้นบรรยากาศและการทำวงโคจรที่มีเสถียรภาพ |
| − | : | + | :จากนิยาม: <math>\Delta{v} = \int_{t_0}^{t_1} {\frac {|T|} {m}}\, dt</math> |
| − | : | + | :เมื่อ''T'' คือแรงขับ, ''m'' คือมวลที่แท้จริง |
| − | : | + | :ถ้าไม่มีแรงภายนอกมากระทำ และทิศทางที่เปลี่ยนไป ผลของการเปลี่ยนแปลงความเร็ว: |
: <math>\Delta{v} = \int_{t_0}^{t_1} {\frac {|T|} {m}}\ dt = \int_{t_0}^{t_1} {|a|}\ dt = | {v}_1 - {v}_0 |\,</math> | : <math>\Delta{v} = \int_{t_0}^{t_1} {\frac {|T|} {m}}\ dt = \int_{t_0}^{t_1} {|a|}\ dt = | {v}_1 - {v}_0 |\,</math> | ||
| − | : | + | :ในกรณีที่มีการคิดถึงแรงพลักจำเพาะ(Specific Impulse): |
: <math>\Delta{v} = | {v}_1 - {v}_0 |_{max}\ = -\int_{t_0}^{t_1} {I_{sp} \cdot g\ \cdot \frac{\dot{m}} {m}}\ dt = {I_{sp} \cdot g \cdot ln( \frac {m_0} {m_1})}\,</math> | : <math>\Delta{v} = | {v}_1 - {v}_0 |_{max}\ = -\int_{t_0}^{t_1} {I_{sp} \cdot g\ \cdot \frac{\dot{m}} {m}}\ dt = {I_{sp} \cdot g \cdot ln( \frac {m_0} {m_1})}\,</math> | ||
| − | ;Energy | + | ;พลังงาน(Energy) |
| − | + | ดูเพิ่มเติมที่ {{Wikipedia|Specific orbital energy}} | |
| − | : | + | :พลังงานของวัตถุทีอยู่บนวงโคจรคือ ผลรวมทั้งหมดของพลังงานศักย์(potential energy) และพลังงานจล (kinetic energy) ซึ่งพลังงานศักย์คือ <math>E_p = -\frac{G M m}{R}</math> และ พลังงานจล คือ<math>E_k = \frac{1}{2} m v^2</math> เมื่อให้ ''G'' คือ [[w:Gravitational constant|ค่าคงตัวแรงโนมถ่วง]], 'M'' คือมวลของ[[celestial body|ดาว]], 'm'' คือมวลของ[[craft | ยาน]], ''R'' คือรัศมีของดาว และ ''v'' คือความเร็วของยาน ทั้งหมดนี้จะได้ผลลัพท์ คือ <math>E = E_k + E_p = \frac{1}{2} m v^2 - \frac{G M m}{R}</math>, ผลรวมนี้จะไม่มีการเปลี่ยนแปลงเมื่อไม่มีแรงขับ (trust) เกิดขึ้น. เมื่อเราเดินทางเข้าใกล้จุดต่ำสุดของวงโคจร (periapsis) พลังงานศักย์จะถ่ายเทไปเป็นพลังงาน จล หลังจากผ่านจุดต่ำสุดของวงโคจร พลังงานจลก็จะถูกถ่ายเทกลับมาเป็นพลังงานศักย์ เมือพลังงาน หรือ ค่าจำเพาะพลังงานวงโคจร มากกว่า 0 ยานจะเข้าสู่วิถีออกจากวงโคจร (escape trajectory) |
| − | : | + | :จากความคิดพื้นฐานจากกฏการเคลื่อนที่ของดาว ของเคปเลอร์ (Kepler's laws of planetry motion) ซึ่งเป็นผลให้เกิดขึ้นของการประมาณการวงโคจร (patched conics approxmation) ซึ่ง วงรีคือเซทของจุนที่อยู่บนระนาบ ที่ผลรวมของระยะทางจากจุดใดๆบนวงรี ถึง จุดโฟกัสสองจุดของวงรี(the foci) จะเป็นค่าคงตัวเสมอ. ซึ่งหนึ่งในโฟกัสของวงโคจรเคปเลอร์ จะอยู่จุดศูนถ่วงของดาวที่โคจรรอบ เมื่อมีวัตถุที่วิ่งเข้าหา จะมีการ แลกเปลี่ยนพลังงานเป็น พลังงานจล และเมื่อวัตถุออกห่างไปจะเปลี่ยนเป็นพลังงานศักย์ และถ้าจุดโฟกัสของวงลี อยู่บนวิถี จะทำให้ พลังงานศักย์ หรือพลังงานจลเป็นศูนย์เสมอ และในกรณีที่ วงโคจรเป็นวงกลมโดยสมบูรณ์ โฟกัสของวงรีก็จะรวมกันที่จุดๆเดียว |
| − | : | + | :ยังมีพลังงานจำเพาะในวงโคจร (<math>\epsilon</math>) ที่ไม่จำเป็นต้องมีมวลของยาน math>E_p = \epsilon_p m</math>, <math>E_k = \epsilon_k m</math>, <math>E = \epsilon \, m = (\epsilon_k + \epsilon_p) m = -\frac{G M}{2 a}</math> และทุกวงโคจรที่มีแกนหลักและรองเหมือนกัน (''a'') ก็จะมีพลังงานจำเพาะวงโคจรเท่ากัน |
| − | ;Escape Velocity | + | ;ความเร็วหลุดพ้น (Escape Velocity) |
| − | : | + | :ความเร็วที่ต้องการในการออกจากแรงดึงดูดของดาวหนึ่งนั้น. โดย <math>v_e = \sqrt{\frac{2GM}{r}},</math> กำหนดให้ G คือ ค่าคงตัวของแรงดึงดูด ([[w:Gravitational constant|gravitational constant]]), M คือ มวลของดาวนั้นๆ และ r คือ รัศมีของดาว |
| − | ;g-force (G) | + | ;แรงจี (g-force (G)) |
| − | : | + | :การวัดค่าอัตราเร่งของแรงดึงดูดโลกมักจะวัดค่าที่อยู่ในระดับน้ำทะเล ด้วยค่า G ประมาณ 9.81 m/s² โดยปกตแล้ววัตถุที่อยู่บนผิวโลกจะมีค่าความเร่งที่ 1 G และวัตถุจะมีน้ำหนักมากขึ้นเป็น 2เท่าตัวเมื่อมีความเร่งเท่ากับ 2 G หรือ วัตถุจะมีสภาพไร้น้ำหนักเมื่อมีความเร่งเท่ากับ 0 G ซึ่งในการตกอย่างอิสระ (free fall) เช่น การอยู่บนวงโคจรและไม่มีการทำงานของเครื่องยนต์ หรือ หรือสิ่งแวดล้อมที่แรงเสียดทานที่ทำให้ความเร่งเป็น 0 แล้วจะแสดงว่าเป็นสภาพ 0 G |
| − | ;Gravity | + | ;แรงโน้มถ่วง (Gravity) |
| − | : | + | :แรงที่กระทำต่อวัตถุทุกชิ้นที่มีมวล ซึ่งมีกำลังน้อยมาก ปกติจะเกิดขึ้นในวิตถุที่มีมวลเยอะมาก เช่น ดาวเคราะห์ ,ดวงจันทร์-อาจจะไม่รับรู้ถึงผลกระทบ เป็นต้น และจะแรงลดลงเป็นกำลังสองของระยะทางจากจุดศูนย์ถ่วงของมวล ดังนั้นเมื่อวัตถุที่ห่างออกไปไกลสองเท่า จะรับรู้ได้เพียง 1/2<sup>2</sup> = 1/4 ของแรงดึงดูดเท่านั้น |
| − | ;Gravity Well | + | ;สนามแรงโน้มถ่วง (Gravity Well) |
| − | : | + | :พื้นที่รอบดาวนั้นจะมีผลกระทบกับแรงโน้มถ่วง และน่าจะมีขอบเขตที่ระยะอนันต์ แต่แรงโนมถ่วงน้ำมีค่าลดลงด้วยค่าทวีคูณจากระยะห่าง (เพียงห่าง 2 เท่าแรงโน้มถ่วงจะลดลงไปถึง 4 เท่า) ทำให้นัยสำคัญของแรงโน้มถ่วงจะกิดขึ้นใกล้ๆกับทรงกลมรอบๆดาวเท่านั้น และใจความจริงของ KSP ไม่สามารถจำลองสภาพที่อยู่เกินออกไปจาก ทรงกลมรอบๆดาวได้ทำให้ต้องใช้ การประมาณการวงโคจร (patched conics approxmation)มาช่วยในการจำลอง |
| − | ;Orbit | + | ;วงโคจร (Orbit) |
{{Main article|Orbit}} | {{Main article|Orbit}} | ||
| − | : | + | :เมื่อวัตถุที่มีความเร็วในมุมที่ขนานกับพื้นดาว(tangential velocity) สูงพอ (และ อยู่นอกชั้นบรรยากาศ เพื่อไม่มีแรงเสียดทานทำให้ช้าลง) ซึ่งทำให้วัตถุนั้นตกลงไปที่หน้าของดาวเสมอ (คือไม่สัมผัสพื้น) และวิถีการเดินทางนี้เรียกว่า วงโคจร ซึ่งวงโคจรที่มีความเสถียจะเป็นวงรี (อาจจะเป็นวงกลมก็ได้) และหาวัตถุนั้นมีความเร็วสูงกว่าความเร็วหลุดพ้น วงโคจรจะถูกเปลี่ยนเป็น พาราโบร่า หรือ ไฮเปอโบร่าฃ |
| − | ;<span id="isp">Specific Impulse (I<sub>sp</sub>)</span> | + | ;<span id="isp">ค่าจำเพาะของแรงดล(Specific Impulse) (I<sub>sp</sub>)</span> |
{{Main article|Specific impulse}} | {{Main article|Specific impulse}} | ||
:<math style="float:center">I_{sp}= \frac{T}{\dot m},</math><span style="padding:1em"></span><math style="float:center"> [I_{sp}] = \frac{m}{s}</math> | :<math style="float:center">I_{sp}= \frac{T}{\dot m},</math><span style="padding:1em"></span><math style="float:center"> [I_{sp}] = \frac{m}{s}</math> | ||
| − | : | + | :เมือนิยาม I<sub>sp</sub> เป็นความคุ้มค่าของเครื่องยนต์ ซึ่งหาก I<sub>sp</sub> มีค่าสูงแสดวงว่าเครื่องยนต์จะให้พลังขับมากกว่าเมื่อเทียบกับการใช้เชื้อเพลิงในปริมาณเท่ากัน โดยปกติแล้ว I<sub>sp</sub>จะอยู่ในหน่วย "วินาที" (S) แต่ที่ถูกต้องทางฟิสิกส์จะมีหน่วยเป็น "ระยะทาง ต่อ วินาที" ซึ่งอาจจะเป็น "เมตร ต่อ วินาที" หรือ "ฟุต ต่อ วินาที" ก็ได้ เพื่อไม่ให้สับสนกับหน่วยของความเร็ว เราจึงนำ I<sub>sp</sub> (ในหน่วย ระยะทาง ต่อ เวลา) หารด้วย แรงโน้มถ่วงของโลก (9.81 m/s²) ซึ่งจะให้ค่าออกมาในหน่วย ของ "วินาที" หากต้องการเปลี่ยน I<sub>sp</sub>กลับมาเป็นหน่วย (ระยะทาง ต่อ เวลา) ก็เพียงนำมาคูณกับแรงโน้มถ่วงของโลกอีกครั้ง ซึ่งค่านี้เอาไว้แปลงระหว่างสองหน่วยนี้ '''ค่าจำเพาะของแรงดล จะไม่เปลี่ยน เมื่อค่าแรงโน้มถ่วงเปลี่ยน''' และใน KSP จะใช้ค่า 9.82 m/s² ซึ่งจะทำให้ใช้เชื่อเพลิงน้อยลงจากการคำนวน |
| − | : | + | :ค่าจำเพาะแรงดล คือ สัดส่วนของ กำลังขับ และ อัตราการใหลของเชื้อเพลิง <math>\frac{Ns}{kg}</math> ซึ่งใช้เป็นหน่วยของค่าจำเพาะแรงดล และการคำนวนอีกรูปแบบหนึ่ง <math>\frac{m}{s} = kg \cdot \frac{m}{s^2} \cdot \frac{s}{kg}</math> เนื่องจาก แรงขับ คือ ผลคูณของ มวล และ ความเร่ง เมื่อนิยาม <math>N = kg \cdot \frac{m}{s^2}</math> แล้ว <math>1 \frac{Ns}{kg} = 1 \frac{m}{s}</math> (อยู่ในหน่วย SI) |
| − | ;<span id="soi">Sphere of influence</span> | + | ;<span id="soi">เขตอิทธิพลแรงโน้มถ่วง (Sphere of influence)</span> |
{{Main article|Sphere of influence}} | {{Main article|Sphere of influence}} | ||
| − | : | + | :คือรัศมีรอบดาวเคราะห์ ซึ่งแรงโน้มถ่วงนั้นมีผลกระทบ โดยทั่วไปจะรู้จักในชื่อว่า SoI/SOI. |
| − | ;Tangential velocity | + | ;ความเร็วเส้นสัมผัส (Tangential velocity) |
| − | : | + | :คือส่วนประกอบของความเร็วที่สัมผัสกับวิถีโคจร ซึ่งความเร็วขณะหนึ่ง เมื่อการวัดเวลาเข้าใกล้ศูนย์ มักจะขนานสัมผัสกับวิถีโคจรเสมอ |
| − | ;<span id="TWR">Thrust-to-weight ratio</span> | + | ;<span id="TWR">อัตราส่วนแรงขับต่อน้ำหนัก (Thrust-to-weight ratio)</span> |
{{See also|Thrust-to-weight ratio}} | {{See also|Thrust-to-weight ratio}} | ||
| − | :<math style="float:right;padding:.5em;">\text{TWR} = \frac{T}{W} = \frac{T}{m \cdot g}</math> | + | :<math style="float:right;padding:.5em;">\text{TWR} = \frac{T}{W} = \frac{T}{m \cdot g}</math> เป็นอัตราส่วนระหว่างมวลทั้งหมดของยาน และแรงขับทั้งหมดในขั้นตอน(Stage)นั้น ซึ้งถ้ามีอัตราส่วนมากกว่า 1 ยานจะมีความสามารถในการเร่งในแนวตั้งและเพิ่มความสูงได้ แต่ถ้าอัตราส่วนน้อยกว่า 1 นั้นยานจะไม่สามารถสู้กับแรงโน้มถ่วง และแรงเสียดทานที่ความสูงระดับต่ำได้ แต่ในอวกาศนั้นจะเป็นเพียงแค่การเปลี่ยนท่าทางการบินที่นานขึ้นกว่าเดิมเท่านั้น เพราะ น้ำหนัก(W) จะขึ้นอยู่กับแรงโน้มถ่วง(g) ทำให้อัตราส่วนแรงขับต่อน้ำหนักจะขึ้นอยู่กับดาวที่มีอิทธิพลกับยานเท่านั้น เช่นความเร่งอยู่บนพื้นผิว [[Mun]] มีเพียงแค่ 16.6 % ของความเร่งที่ Kerbin ดังนั้น ที่พื้นผิว TWR<sub>Kerbin</sub> = 1 จะทำให้ TWR<sub>Mun</sub> = 6. |
| − | ;Trajectory | + | ;วิถีโคจร (Trajectory) |
| − | : | + | :วิถีโคจร คือเส้นทางที่วัตถุเคลื่อนที่ผ่านอวกาศในฟังค์ชั่นของเวลา |
| − | ;Velocity | + | ;ความเร็ว (Velocity) |
| − | : | + | :อัตราการเปลี่ยนแปลงของตำแหน่ง ซึ่งประกอบด้วย อัตราเร็ว และทิศทาง ซึ่งความเร็วนั้นเป็นเว็กเตอร์ มีหน่วยเป็น เมตรต่อวินาที (m/s) |
==See also== | ==See also== | ||
| Line 177: | Line 180: | ||
* [[Acronyms and Initialisms]] | * [[Acronyms and Initialisms]] | ||
* [[Deep Space Kraken]] | * [[Deep Space Kraken]] | ||
| + | |||
| + | [[Category:Thai Language pages]] | ||
Latest revision as of 01:28, 25 November 2021
KSP มีคำศัพท์หลายคำที่เกี่ยวข้องกับ วงโคจรและฟิสิกส์ที่ใช้บ่อยและอาจสับสนกับคำศัพท์ธรรมดา และยังมีคำศัพท์ทางวิทยาศาสตร์และตัวย่อที่มักจะใช้ในอธิบายภายในเกมส์
หน้านี้ได้ถูกออกแบบมาให้กระชับในการค้นหาคำศัพท์ต่างที่จะช่วยคุณเรียนรู้เพื่อจะเป็นนักบินอวกาศมากความสามารถในอนาคต
Contents
คณิตศาสตร์
- วงรี (Elliptical)
- รูปทรงวงรี ส่วนมากใช้บอกถึงลักษณะวิถีวงโคจรที่เป็นรูปวงรี
- ไฮเปอร์โบลา (Hyperbolic)
- เส้นวิถีโค้งปลายเปิด ปกติจะเป็นการแสดงวิถีออกจากวงโคจร(escape trajectories)
- เว็กเตอร์ตั้งฉาก (Normal vector)
- เวกเตอร์ที่ตั้งฉากกับยานอวกาศของคุณ
- สเกลาร์ (Scalar)
- เป็นหน่วยที่มีขนาด แต่ไม่มีทิศทาง, ซึ่งจำนวนสเกลาร์มักจะใช้ในหน่วยที่วัดต่างๆ เช่น 3 m/s (เมตร/วินาที), 3 m(เมตร),3 s(วินาที) เป็นต้น ซึ่งหน่วยต่างๆดังกล่าว จะบอกถึงค่าของความเร็ว ความยาว หรือเวลา แต่จะไม่บอกทิศทางของหน่วยนั้นๆ
- เว็กเตอร์ (Vector)
- เป็นหน่วยที่่มีทั้งขนาดและทิศทาง เช่น ทิศทางการบิน(Heading) และอัตราเร็ว(Speed) และจะได้ ความเร็ว(Velocity). เว็กเตอร์จะถูกเขียนได้หลายแบบซึ่งขึ้นอยู่กับระบบพิกัด(Coordinate system) เช่น <35°, 12> คือเว็กเตอร์เชิงขั้วสองมิติ หรือ <14, 9, -20> เวกเตอร์คาร์ทีเซียนสามมิติ นอกจากนี้ยังมีระบบพิกัดอีกหลายแบบ แต่สองแบบนี้มักจะใช้บ่อยที่สุด
- <35°, 12> หน้าตาคล้ายกับลูกศรที่ยาว 12 หน่วย และเริ่มจากจุดเริ่มต้นทำมุม 35° กับแกนฐานของจุดเริ่มต้น (โดยปกติจะวัดทำมุมกับแกน x และวัดทวนเข็มนาฬิกา)
- <14, 9, -20> หน้าตาคล้ายกับลูกศรที่มีจุดเริ่มต้น (<0,0,0>) และจุดสุดท้ายมีพิกัดที่แกน x ที่ 14 หน่วย แกน y ที่ 9 หน่วย และแกน z ที่ -20
- ข้อดีของการใช้เว็กเตอร์แบบต่างๆ เว็กเตอร์คาร์ทีเซียนจะสามารถบอกจตำแหน่งสุดท้ายได้ แต่จะยากในหาความยาวของเว็กเตอร์ แต่สำหรับเว็กเตอร์เชิงขั้วจะง่ายมากในการหาความยาวของเว็กเตอร์แต่จะยากในการหาตำแหน่งสุดท้ายของเว็กเตอร์
- เว็กเตอร์ต่างๆที่ใช้ในทางฟิสิกส์: ความเร็ว (velocity), ความเร่ง (acceleration), แรง (force)
ระนาบสามมิติ ต้องการ:
- จุดอ้างอิง ส่วนมากคือจุดเริ่มต้น (<0,0,0>)
- 3 เว็กเตอร์ฐาน จะเป็นตัวกำหนดหน่วยฐานในการวัดในแนวแกนต่างๆ (แกน x,y,z)
- การผสมของสเกลาร์ 3 ตัว อาจจะเป็นได้ทั้ง มุม หรือพิกัด ที่จะสามารถแสดง ตำแหน่งในระนาบได้
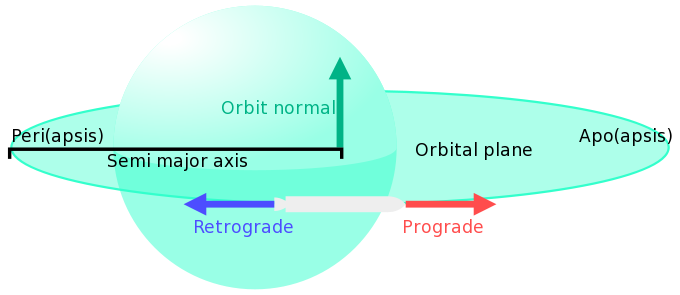
ศัพท์เกี่ยวกับวงโคจร
- จุดไกลที่สุด (Apoapsis)
- จุดใกล้ที่สุด (Periapsis)
- Apsis
- → See also: “Apoapsis and periapsis” section in Orbit
- ทุกวงโคจรที่เป็นวงรี จะมีสองด้านเสมอ(2 apsides). periapsis (q) คือจุดที่ใกล้กับดาวมากที่สุดในวงโคจร (จุดต่ำที่สุดในวงโคนจร) และ apoapsis (Q) จุดที่อยู่ตรงข้างในวงโคจร และมีระยะใกลที่สุดจากดาวในวงโคจร (จุดสูงสุดในวงโคจร). apsides ปกติจะเป็นค่าความสูงจากพื้นผิวของดาว แต่การคำนวนต่างๆจะต้องคิดจากจุดศูนย์กลางของดาวเสมอ เพราะฉนั้นเราจำเป็นต้องบวกรัศมีของดาวเข้าไปในการคำนวนเสมอ
- Peri-* and Apo-*
- ในการพูดเกี่ยวกับวงโคจร, บางครั้งคำว่า "periapsis" และ"apoapsis" อาจจะถูกดัดแปลงเพื่อเรียกเฉพาะกับดาวหรือดวงจันทร์ที่มีวงโคจรอยู่รอบๆ ตัวอย่างเช่น -kee และ -kerb มักจะใช้ในการอ้างถึงวงโคจรรอบๆ Kerbin และทำให้เกิดคำว่า Perikee/Perikerb and Apokee/Apokerb เป็นต้น
- จุดตัดขึ้น (Ascending node)
- จุดตัด(orbital node) ที่ทำให้การเคลื่อนที่มุ่งไปทางทิศเหนือ (เหนือในที่นี้คือ ทิศทางที่ตั้งฉากกับวงโคจร (Orbital Normal))
- จุดตัดลง (Descending node)
- จุดตัด(orbital node) ที่ทำให้การเคลื่อนที่มุ่งไปทางทิศใต้
- ความรี (Eccentricity)
- → See also: “Eccentricity” section in Orbit
- หน่วยสเกล่าที่อธิบายถึงความไม่กลมของวงโคจร ดังนี้
- ecc = 0 → วงโคจรแบบกลม.
- 0 < ecc < 1 → วงโคจรแบบวงรี.
- ecc = 1 → วงโคจรแบบพาราโบลา - วิถีออกจากวงโคจร
- ecc > 1 → วงโคจรแบบไฮเปอร์โบลา - วิถีออกจากวงโคจร
- ความเอียง (Inclination)
- → See also: “Inclination” section in Orbit
มุมที่ทำระหว่างระนาบวงโคจรกับระนาบอ้างอิง (เช่น วงโคจรที่มีความเอียง 90° กับระนาบเส้นศูนย์สูตร จะเรียกว่า โพลา (polar))
- วงโคจรระดับต่ำ (Low orbit)
- วงโคจรที่สูงพอที่จะไม่ถูกรบกวนจากสภาวะแวดล้อมของดาว เช่น แรงเสียดทานจากชั้นบรรยากาศ เป็นต้น วงโคจรระดับต่ำมักจะใช้เป็นบันไดพักขั้นแรกหลังจากที่เราทำการเพิ่มความสูงและก่อนที่จะทำการจุดเครื่องยนต์เพื่อจะไปยังดวงดาว หรือวัตถุอื่นๆในอวกาศ. ทั้งยังสามารถทำการจุดเครื่องยนต์ไปได้ในทุกทิศทาง และต้องการเชื้อเพลิงไม่มากในการมาถึงจากพื้นผิวของดาว วงโคจรระดับต่ำสำหรับ Kerbin นั้นอยู่ระหว่างประมาณ 80 -100 กิโลเมตร สำหรับดาวที่ไม่มีชั้นบรรยากาศสามารถทำวงโคจรในทางทฤษฎี ได้ทุกความสูงเหนือพื้นผิว แต่การทำวงโคจรที่ต่ำกว่าระดับ 10 กิโลเมตรนั้นมีความเสี่ยงที่จะชนกับภูเขาหรือพื้นผิวที่มีความสูงมาก ส่วน time warp จะมีข้อจำกัดในการบินในวงโคจรระดับต่ำ
- จุดตัด (Orbital node) ความหมายในทางอวกาศ(astronomical definition)
- จุดที่วงโคจรตัดผ่านระนาบอ้างอิง ณ จุดตัดขึ้น จุดตัดขึ้น (ascending node) ยานจะเคลื่อนผ่านระนาบอ้างอิงในทิศตั้งฉากกับวงโคจร(Orbital Normal) โดยปกติแล้วจุดขึ้นมักจะชี้ไปทางทิศเหนือและจุดลงจะชี้ไปยังทิศใต้
- จุดตัด (Orbital nodes) ภายในเกมส์(as in game)
- จุดอ้างอิงจำเพาะทุกจุดที่อยู่บนวงโคจรเช่น จุดไกลสุด (Apoapsis), จุดใกล้สุด (Periapsis),จุดตัดกับวงโคจรอื่น เป็นต้น
- ทิศตั้งฉากกับวงโคจร (Orbit normal)
- เว็กเตอร์ตั้งฉากกับระนาบวงโคจร โดยปกติจะเกิดจากผลคูณไขว้ของความเร็วยานกับแรงโน้มท่วง และทำให้เว็กเตอร์สอดคล้องกับกฏมีอขวา จากมุมมองที่ยานทำวงโคจรทวนเข็มนาฬิกาเว็กเตอร์นี้จะชี้ขึ้น ในทางตรงกันข้ามถ้ายานทำวงโคจรตามเข็มนาฬิกาเว็กเตอร์จะชี้ลง โดยปกติแล้ว "ขึ้น" มักจะถูกเรียกว่า "ทิศเหนือ(North)" หรือ "N+" ในส่วนของ "ลง" มักจะเรียกว่า "Anti-Normal","ใต้ (South)" หรือ "N-"
- ระนาบวงโคจร (Orbital plane)
- แผ่นกลมในจินตนาการโดยเป็นวิถีของวงโคจรรอบดาว (โดยปกติใช้ใช้อธิบายความเอียง)
- อัตราเร็ววงโคจร (Orbital speed)
- อัตราเร็วของการโคจรของดาวใดๆนั้น คือความเร็วที่โคจรรอบศูนย์กลางแรงโน้มท่วงของระบบ, โดยปกติจะเป็นดาวที่มีมวลมหาศาล และยังสามารถหมายถึงความเร็วในการทำวงโคจร เช่น ค่าเฉลี่ยความเร็วที่สามารถทำให้วงโคจรสมบูลย์ หรือความเร็วในจุดใดจุดหนึ่งบนวงโคจร
- ทิศเดินหน้า Prograde
- ทิศทางที่ยานเดินทางตามวิถีของวงโคจร เมื่อวงโคจรเป็นวงรี มันมักจะเป็นเส้นสัมผัส(Tangent)กับวิถีวงโคจร ณจุดที่ยานอยู่
- ทิศถอยหลังRetrograde
- ส่วนกลับของทิศเดินหน้า จะย้อนกลับตามวิถีวงโคจร
- ระนาบอ้างอิง (Reference plane)
- ทุกระนาบที่ใช้เป็นระนาบอ้างอิงเพื่อจะอธิบายวงโคจรปัจจุบันของคุณ สำหรับวงโคจรรอบดาวเคราะห์ มักจะใช้ระนาบเส้นศูนย์สูตร(Equatorial plane)เป็นระนาบอ้างอิง หากมีดาวหลายๆในระบบสุริยะระนาบวงรีก็สามารถใช้ได้ สำหรับการตัดกันของวงโคจรของดาว วงโคจรของดาวที่กำลังจะตัดกันอาจจะใช้เป็นระนาบอ้างอิงได้ ระนาบวงโคจรสามารถให้ข้อมูลเกี่ยวกับ ความเอียง และ เส้นแวงของจุดขึ้น ที่สัมพันธ์กับระนาบอ้างอิงได้
- ระยะกึ่งแกนเอก (Semi-major axis)
- → See also: “Semi-major axis” section in Orbit
- แกนเอกคือแกนที่ยาวที่สุดของวงรี และระยะกึ่งแกนเอก(a)คือระยะครึ่งหนึ่งของแกนเอก ซึ่งจะเป็นค่าเฉลี่ยของจุดสูงสุด(Apoapsis) (Q) และจุดต่ำสุด (Periapsis)(q) ที่คำนวนจากศูนย์กลางของดาว ซึ่งทั้งสองสัมพันธ์กับพื้นผิวของดาว โดยที่รัศมีของดาว (R) จำเป็นต้องบวกเข้าไปด้วย และทุกๆวงโคจรที่มีระยะกึ่งแกนเอกเท่ากันจะมีคาบเวลาวงโคจรเท่ากัน โดยไม่คำนึงถึงความรีของวงโคจร
- คาบดาราคติ (Sidereal period)
- คาบดาราคิติคือคาบเวลาขณะหนึ่งที่วัตถุทำวงโคจรครบรอบ เมื่อเทียบกับดวงดาว ซึ่งเป็นคาบวงโคจรที่ใช้แรงเฉื่อยเป็นกรอบการอ้างอิง(ไม่ใช้การหมุน)
- วงโคจรย่อย (Sub-orbital)
- การอธิบายวงโคจรที่จุดต่ำสุด(Periapsis)นั้นอยู่ใต้พิ้นผิวของดาวนั้นๆ ถ้าเรายังเดินทางตามวิถีของวงโคจรย่อยเราก็จะกลับมาชนกับดาวที่เราทำวงโคจรอยู่
- คาบซินโนดิค (Synodic period)
- คาบซินโนดิคคือคาบเวลาขณะหนึ่งที่ทำให้วัตถุนั้นกลับมาอยู่ในตำแหน่งเดิมที่มีความสัมพันธ์ตั้งแต่ สองขึ้นไป ตัวอย่างเช่น เมื่อ Mun มีความสัมพันธ์กับ Kerbol และหาสังเกตการจาก Kerbin ในแต่ละคาบเราจะกลับมาอยู่เฟสด้านสว่างเหมือนกัน คาบซินโนดิคคือเวลาที่ผ่านไประหว่างวัตถุสองวัตถุ และมีสันธานร่วมกันอย่างสมบูลย์ที่ Kerbol - Kerbin เรียงตัวกันในแนวเส้นตรงตามลำดับ ซึ่ง คาบซินโนดิคจะต่างจากคาบดาราคติตรงที่การโคจรของ Kerbin รอบๆ Kerbol
ทิศทางของยาน (Ship Orientation)
ทิศทางของยานปกติจะต้องมีความสัมพันธ์กับวัตถุใดวัตถุหนึ่ง โดยปกติจะอ้างอิงกับ ห้องนักบิน The ship orientation is always relative to a specific object. The terms are usually defined relative to the cockpit.
- จุดสูงสุด (Zenith)
- ด้านบนของบาน ปกติจะอยู่ห่างจากดาวที่ทำวงโคจรอยู่ และอยู่ตรงข้ามกับจุดต่ำสุด (nadir)
- จุดต่ำสุด (Nadir)
- ด้านล่างของยานซึ่งปกติจะหันไปทางดาวที่ทำวงโคจรอยู่ และอยู่ตรงข้ามกับจุดสูงสุด (Zenith)
- พอร์ท (Port(side))
- ด้านซ้ายของตัวยาน ตรงข้ามกัน สตาร์บอร์ด(Starboard)
- สตาร์บอร์ด (Starboard)
- ด้านขวาของตัวยาน ตรงกันข้ามกันพอร์ท(Portside)
- ด้านหน้า (Front)
- ด้านหน้าของยานปกติจะอยู่ทางจมูกยานหรือเว็กเตอร์ทิศเดินหน้า(Prograde)
- อัฟท์ (Aft)*
- ด้านหลังโดยปกติจะเป็นที่อยู่ของเครื่องยนต์หลัก และหันหน้าไปทาง ทิศย้อนกลับ(Retrograde)
การเคลื่อนในอวกาศ (Space Maneuvers)
- เบรคด้วยชั้นบรรยากาศ (Atmospheric braking)
- → Main article: Aerobraking
- ลดระดับของจุดต่ำสุด(Periapsis) ให้อยู่ในระยะของชั้นบรรยากาศของดาว การกระทำเช่นนี้จะทำให้ยานสามารถลดความเร็วจากแรงเสียดทานในชั้นบรรยากาศได้ และยังสามารถนำไปสู่การกับเข้าชั้นบรรยากาศได้อีกด้วยซึ่งช่วยลดการใช้เชื้อเพลิงในการเปลี่ยนรูปแบบวงโคจร
Lowering the periapsis so it is inside a planetary atmosphere. This will lead to the vessel being slowed by atmospheric drag. Can lead to atmospheric entry, but also is used to reduce the necessary burn time for significant orbit alterations.
- ลิโทรเบรคกิ้ง (Lithobraking)
- → See also: Lithobraking on Wikipedia
- แทนที่เราจะใช้อากาศในการช่วยเบรค แต่นี้เราใช้ "พื้น" แทนอากาศ ปกติเราจะใช้คำเพื่อล้อเลียนการลงแบบตกกระแทกพื้น ซึ่งไม่ได้อยู่ในแผนที่วางไว้ ซึ่งคำนี้เกิดจากการผวนมาจากคำว่า "Aerobreaking" โดยที่เปลี่ยนจาก "Aero" มาเป็น "lithos" ซึ่งแปลว่า หิน ในภาษากรีก
- เข้าสู่ชั้นบรรยากาศ (Atmospheric entry)
- → Main article: Atmospheric entry
- การเข้าสู่ชั้นบรรยากาศและใช้แรงเสียดทานในการลดความเร็วของยาน เพื่อให้เข้าสู่วิถีลงพื้น. ในโลกความจริงของวิทยาศาสตร์ นี้จะสร้างความเครียดที่เกิดจากความร้อนบนวัตถุ ฉนั้นยานจะต้องมีความเร็วที่เพียงพอที่จะไม่เด้งกลับไปยังอวกาศอีกครั้ง ปัจจุบันการเข้าสู่บรรยากาศในเกมส์ยังพัฒนาเพียงส่วนหนึ่งมีเพียงผลกระทบบางอย่าง แต่ไม่รวมถึงความร้อนและการเด้งออกสู่อวกาศยังไม่ถูกพัฒนา แต่ก็สามารถใช้ ส่วนเสริมของเกมส์ที่สามารถทำให้ชิ้นส่วนยานร้อนเกินไปได้ (overheat) และปกติจะเรียกว่า รีเอ็นทรี่(re-entry/reentry)
- เบิร์น (Burn)
- การจุดเครื่องยนต์ ,ใช้ในการเปลี่ยนวิถีการบิน
- เซอร์เคิลไลซิงก์(Circularizing)
การลดความรี(eccentricity)ของวงโคจรให้เข้าใกล้ 0 มากที่สุด ส่วนมาจะเบิร์นใกล้ๆ จุด apsis
- Reducing an orbit's eccentricity to 0 or close to it. This is usually achieved by a burn close to an apsis.
- จุดเปลี่ยนทิศทาง (Maneuver node)
- → Main article: Maneuver node
- เป็นการวางแผนการเปลี่ยนเส้นทางบนแผนที่ จึงต้องใช้ burn ในการทำ.
- เบิร์นเข้าสู่ศูนย์กลาง(Radial-in burn)
- การเบิร์นเข้าสู่ศูนย์กลางของดาวเคราะห์ และจะทำการหมุนวงโคจร ทวนเข็มนาฬิกาจนกว่าจุดต่ำสุด(Periapsis)จะผ่านจุดศูนย์ถ่วงของดาวเคราะห์ และตรงข้ากับเบิร์นออกจากศูนย์กลาง
- เบิร์นออกจากศูนย์กลาง(Radial-out burn)
- การเบิร์นออกจากศูนย์กลางดาวเคราะห์โดยตรง และจะทำให้การหมุนวงโคจร หมนตามเข็มนาฬิกาจนจุดต่ำสุด(Periapsis)จะผ่านจุดศูนย์ถ่วงของดาวเคราะห์
- Radial burn
- → See also: Maneuver node
- Re-entry
- → See also: Atmospheric entry
- รีโทรเบิร์น(Retroburn)
- การเบิร์นที่ทำให้เกิดการ "ถอยหลัง", เช่น การทำให้เครื่องยนหันไปทางด้านหน้า(Prograde) และด้านหน้าหักไปทางด้านหลัง(Retrograde) โดยปกติจะใช้ท่าการบินนี้สำหรับการลดระดับจุดต่ำสุด(periapsis) และจุดสูงสุด(apoapsis)
ฟิสิกค์(Physics)
- ความเร่ง(Acceleration)
- อัตราการเปลี่ยนแปลงของความเร็ว(Velocity), ความเร่งเป็นเว็คเตอร์ และมีหนวยเป็น "m/s2"
- วิถีกระสุน(Ballistic trajectory)
- การร่วงหล่นของวัตถุจะมีวิธีที่เป็นวิถีแบบกระสุน ในเรื่องที่เกี่ยวกับจรวดจะแสดงถึงวัตถุที่มีปฏิสัมพันธ์กับแรงดึงดูดเท่านั้นและไม่มีแรงอื่นมากระทำไม่เว้นแม้แต่แรงขับจรวด
- เดลต้าวี(Delta-v (Δv))
- การเปลี่ยนของความเร็วที่กำเนิดมาจากยานอวกาศ และมีหน่วยในการวัดเป็นเมตรต่อวินาที(m/s) มวลที่มากขี้นจะลดเดลต้าวีให้ลดลง แต่หากมีแรงขับมากขึ้นจะสามารถเพิ่มเดลต้าวีได้ ค่านี้เป็นค่าที่สำคัญในการคำนวนความคุ้มค้าและประสิทธิภาพของจรวด ตัวอย่างเช่น การยิงยานต้องการเดลต้าวีประมาณ 4500 m/s ในการออกจากชั้นบรรยากาศและการทำวงโคจรที่มีเสถียรภาพ
- จากนิยาม:
- เมื่อT คือแรงขับ, m คือมวลที่แท้จริง
- ถ้าไม่มีแรงภายนอกมากระทำ และทิศทางที่เปลี่ยนไป ผลของการเปลี่ยนแปลงความเร็ว:
- ในกรณีที่มีการคิดถึงแรงพลักจำเพาะ(Specific Impulse):
- พลังงาน(Energy)
ดูเพิ่มเติมที่ Specific orbital energy on Wikipedia
- พลังงานของวัตถุทีอยู่บนวงโคจรคือ ผลรวมทั้งหมดของพลังงานศักย์(potential energy) และพลังงานจล (kinetic energy) ซึ่งพลังงานศักย์คือ และ พลังงานจล คือ เมื่อให้ G คือ ค่าคงตัวแรงโนมถ่วง, 'M คือมวลของดาว, 'm คือมวลของ ยาน, R คือรัศมีของดาว และ v คือความเร็วของยาน ทั้งหมดนี้จะได้ผลลัพท์ คือ , ผลรวมนี้จะไม่มีการเปลี่ยนแปลงเมื่อไม่มีแรงขับ (trust) เกิดขึ้น. เมื่อเราเดินทางเข้าใกล้จุดต่ำสุดของวงโคจร (periapsis) พลังงานศักย์จะถ่ายเทไปเป็นพลังงาน จล หลังจากผ่านจุดต่ำสุดของวงโคจร พลังงานจลก็จะถูกถ่ายเทกลับมาเป็นพลังงานศักย์ เมือพลังงาน หรือ ค่าจำเพาะพลังงานวงโคจร มากกว่า 0 ยานจะเข้าสู่วิถีออกจากวงโคจร (escape trajectory)
- จากความคิดพื้นฐานจากกฏการเคลื่อนที่ของดาว ของเคปเลอร์ (Kepler's laws of planetry motion) ซึ่งเป็นผลให้เกิดขึ้นของการประมาณการวงโคจร (patched conics approxmation) ซึ่ง วงรีคือเซทของจุนที่อยู่บนระนาบ ที่ผลรวมของระยะทางจากจุดใดๆบนวงรี ถึง จุดโฟกัสสองจุดของวงรี(the foci) จะเป็นค่าคงตัวเสมอ. ซึ่งหนึ่งในโฟกัสของวงโคจรเคปเลอร์ จะอยู่จุดศูนถ่วงของดาวที่โคจรรอบ เมื่อมีวัตถุที่วิ่งเข้าหา จะมีการ แลกเปลี่ยนพลังงานเป็น พลังงานจล และเมื่อวัตถุออกห่างไปจะเปลี่ยนเป็นพลังงานศักย์ และถ้าจุดโฟกัสของวงลี อยู่บนวิถี จะทำให้ พลังงานศักย์ หรือพลังงานจลเป็นศูนย์เสมอ และในกรณีที่ วงโคจรเป็นวงกลมโดยสมบูรณ์ โฟกัสของวงรีก็จะรวมกันที่จุดๆเดียว
- ยังมีพลังงานจำเพาะในวงโคจร () ที่ไม่จำเป็นต้องมีมวลของยาน math>E_p = \epsilon_p m</math>, , และทุกวงโคจรที่มีแกนหลักและรองเหมือนกัน (a) ก็จะมีพลังงานจำเพาะวงโคจรเท่ากัน
- ความเร็วหลุดพ้น (Escape Velocity)
- ความเร็วที่ต้องการในการออกจากแรงดึงดูดของดาวหนึ่งนั้น. โดย กำหนดให้ G คือ ค่าคงตัวของแรงดึงดูด (gravitational constant), M คือ มวลของดาวนั้นๆ และ r คือ รัศมีของดาว
- แรงจี (g-force (G))
- การวัดค่าอัตราเร่งของแรงดึงดูดโลกมักจะวัดค่าที่อยู่ในระดับน้ำทะเล ด้วยค่า G ประมาณ 9.81 m/s² โดยปกตแล้ววัตถุที่อยู่บนผิวโลกจะมีค่าความเร่งที่ 1 G และวัตถุจะมีน้ำหนักมากขึ้นเป็น 2เท่าตัวเมื่อมีความเร่งเท่ากับ 2 G หรือ วัตถุจะมีสภาพไร้น้ำหนักเมื่อมีความเร่งเท่ากับ 0 G ซึ่งในการตกอย่างอิสระ (free fall) เช่น การอยู่บนวงโคจรและไม่มีการทำงานของเครื่องยนต์ หรือ หรือสิ่งแวดล้อมที่แรงเสียดทานที่ทำให้ความเร่งเป็น 0 แล้วจะแสดงว่าเป็นสภาพ 0 G
- แรงโน้มถ่วง (Gravity)
- แรงที่กระทำต่อวัตถุทุกชิ้นที่มีมวล ซึ่งมีกำลังน้อยมาก ปกติจะเกิดขึ้นในวิตถุที่มีมวลเยอะมาก เช่น ดาวเคราะห์ ,ดวงจันทร์-อาจจะไม่รับรู้ถึงผลกระทบ เป็นต้น และจะแรงลดลงเป็นกำลังสองของระยะทางจากจุดศูนย์ถ่วงของมวล ดังนั้นเมื่อวัตถุที่ห่างออกไปไกลสองเท่า จะรับรู้ได้เพียง 1/22 = 1/4 ของแรงดึงดูดเท่านั้น
- สนามแรงโน้มถ่วง (Gravity Well)
- พื้นที่รอบดาวนั้นจะมีผลกระทบกับแรงโน้มถ่วง และน่าจะมีขอบเขตที่ระยะอนันต์ แต่แรงโนมถ่วงน้ำมีค่าลดลงด้วยค่าทวีคูณจากระยะห่าง (เพียงห่าง 2 เท่าแรงโน้มถ่วงจะลดลงไปถึง 4 เท่า) ทำให้นัยสำคัญของแรงโน้มถ่วงจะกิดขึ้นใกล้ๆกับทรงกลมรอบๆดาวเท่านั้น และใจความจริงของ KSP ไม่สามารถจำลองสภาพที่อยู่เกินออกไปจาก ทรงกลมรอบๆดาวได้ทำให้ต้องใช้ การประมาณการวงโคจร (patched conics approxmation)มาช่วยในการจำลอง
- วงโคจร (Orbit)
- → Main article: Orbit
- เมื่อวัตถุที่มีความเร็วในมุมที่ขนานกับพื้นดาว(tangential velocity) สูงพอ (และ อยู่นอกชั้นบรรยากาศ เพื่อไม่มีแรงเสียดทานทำให้ช้าลง) ซึ่งทำให้วัตถุนั้นตกลงไปที่หน้าของดาวเสมอ (คือไม่สัมผัสพื้น) และวิถีการเดินทางนี้เรียกว่า วงโคจร ซึ่งวงโคจรที่มีความเสถียจะเป็นวงรี (อาจจะเป็นวงกลมก็ได้) และหาวัตถุนั้นมีความเร็วสูงกว่าความเร็วหลุดพ้น วงโคจรจะถูกเปลี่ยนเป็น พาราโบร่า หรือ ไฮเปอโบร่าฃ
- ค่าจำเพาะของแรงดล(Specific Impulse) (Isp)
- → Main article: Specific impulse
- เมือนิยาม Isp เป็นความคุ้มค่าของเครื่องยนต์ ซึ่งหาก Isp มีค่าสูงแสดวงว่าเครื่องยนต์จะให้พลังขับมากกว่าเมื่อเทียบกับการใช้เชื้อเพลิงในปริมาณเท่ากัน โดยปกติแล้ว Ispจะอยู่ในหน่วย "วินาที" (S) แต่ที่ถูกต้องทางฟิสิกส์จะมีหน่วยเป็น "ระยะทาง ต่อ วินาที" ซึ่งอาจจะเป็น "เมตร ต่อ วินาที" หรือ "ฟุต ต่อ วินาที" ก็ได้ เพื่อไม่ให้สับสนกับหน่วยของความเร็ว เราจึงนำ Isp (ในหน่วย ระยะทาง ต่อ เวลา) หารด้วย แรงโน้มถ่วงของโลก (9.81 m/s²) ซึ่งจะให้ค่าออกมาในหน่วย ของ "วินาที" หากต้องการเปลี่ยน Ispกลับมาเป็นหน่วย (ระยะทาง ต่อ เวลา) ก็เพียงนำมาคูณกับแรงโน้มถ่วงของโลกอีกครั้ง ซึ่งค่านี้เอาไว้แปลงระหว่างสองหน่วยนี้ ค่าจำเพาะของแรงดล จะไม่เปลี่ยน เมื่อค่าแรงโน้มถ่วงเปลี่ยน และใน KSP จะใช้ค่า 9.82 m/s² ซึ่งจะทำให้ใช้เชื่อเพลิงน้อยลงจากการคำนวน
- ค่าจำเพาะแรงดล คือ สัดส่วนของ กำลังขับ และ อัตราการใหลของเชื้อเพลิง ซึ่งใช้เป็นหน่วยของค่าจำเพาะแรงดล และการคำนวนอีกรูปแบบหนึ่ง เนื่องจาก แรงขับ คือ ผลคูณของ มวล และ ความเร่ง เมื่อนิยาม แล้ว (อยู่ในหน่วย SI)
- เขตอิทธิพลแรงโน้มถ่วง (Sphere of influence)
- → Main article: Sphere of influence
- คือรัศมีรอบดาวเคราะห์ ซึ่งแรงโน้มถ่วงนั้นมีผลกระทบ โดยทั่วไปจะรู้จักในชื่อว่า SoI/SOI.
- ความเร็วเส้นสัมผัส (Tangential velocity)
- คือส่วนประกอบของความเร็วที่สัมผัสกับวิถีโคจร ซึ่งความเร็วขณะหนึ่ง เมื่อการวัดเวลาเข้าใกล้ศูนย์ มักจะขนานสัมผัสกับวิถีโคจรเสมอ
- อัตราส่วนแรงขับต่อน้ำหนัก (Thrust-to-weight ratio)
- → See also: Thrust-to-weight ratio
- เป็นอัตราส่วนระหว่างมวลทั้งหมดของยาน และแรงขับทั้งหมดในขั้นตอน(Stage)นั้น ซึ้งถ้ามีอัตราส่วนมากกว่า 1 ยานจะมีความสามารถในการเร่งในแนวตั้งและเพิ่มความสูงได้ แต่ถ้าอัตราส่วนน้อยกว่า 1 นั้นยานจะไม่สามารถสู้กับแรงโน้มถ่วง และแรงเสียดทานที่ความสูงระดับต่ำได้ แต่ในอวกาศนั้นจะเป็นเพียงแค่การเปลี่ยนท่าทางการบินที่นานขึ้นกว่าเดิมเท่านั้น เพราะ น้ำหนัก(W) จะขึ้นอยู่กับแรงโน้มถ่วง(g) ทำให้อัตราส่วนแรงขับต่อน้ำหนักจะขึ้นอยู่กับดาวที่มีอิทธิพลกับยานเท่านั้น เช่นความเร่งอยู่บนพื้นผิว Mun มีเพียงแค่ 16.6 % ของความเร่งที่ Kerbin ดังนั้น ที่พื้นผิว TWRKerbin = 1 จะทำให้ TWRMun = 6.
- วิถีโคจร (Trajectory)
- วิถีโคจร คือเส้นทางที่วัตถุเคลื่อนที่ผ่านอวกาศในฟังค์ชั่นของเวลา
- ความเร็ว (Velocity)
- อัตราการเปลี่ยนแปลงของตำแหน่ง ซึ่งประกอบด้วย อัตราเร็ว และทิศทาง ซึ่งความเร็วนั้นเป็นเว็กเตอร์ มีหน่วยเป็น เมตรต่อวินาที (m/s)
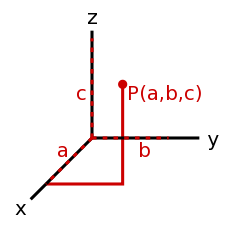
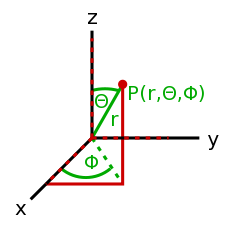













![{\displaystyle [I_{sp}]={\frac {m}{s}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/072515563895cdf8f2d19f1dab433618230ce14f)




