Difference between revisions of "Terminology/zh-cn"
From Kerbal Space Program Wiki
(→另见) |
|||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 10: | Line 10: | ||
;双曲线(Hyperbolic) | ;双曲线(Hyperbolic) | ||
:开放的光滑曲线,通常对应的是逃逸轨道。 | :开放的光滑曲线,通常对应的是逃逸轨道。 | ||
| − | ; | + | ;法向量(Normal Vector) |
| − | : | + | :一条与平面垂直的向量。(在赤道轨道上,法向量指向北极的方向) |
;标量(scalar) | ;标量(scalar) | ||
:一个没有方向的数值。标量一般会有测量单位的后缀,表明这个标量的量纲。 比如 3 米每秒(m/s), 3 米(m),3 秒(s) 都是标量:它们分别是速率(区分于速度)、路程(区分于位移)和时间的单位,但不含方向。 | :一个没有方向的数值。标量一般会有测量单位的后缀,表明这个标量的量纲。 比如 3 米每秒(m/s), 3 米(m),3 秒(s) 都是标量:它们分别是速率(区分于速度)、路程(区分于位移)和时间的单位,但不含方向。 | ||
| Line 26: | Line 26: | ||
一个三维坐标系需要: | 一个三维坐标系需要: | ||
| − | * | + | * 一个参考系原点。 |
* 3个单位向量。这些向量定义了沿着坐标轴的基本量度和坐标轴的方向。 | * 3个单位向量。这些向量定义了沿着坐标轴的基本量度和坐标轴的方向。 | ||
* 3个标量,这可以是角度或坐标,用来描述坐标空间中的位置。 | * 3个标量,这可以是角度或坐标,用来描述坐标空间中的位置。 | ||
| Line 39: | Line 39: | ||
;拱点 | ;拱点 | ||
{{See also|Orbit|section=Apoapsis and periapsis}} | {{See also|Orbit|section=Apoapsis and periapsis}} | ||
| − | :每个椭圆轨道都有两个拱点。'''periapsis''' (<tt>q</tt>)(近拱点)是距离轨道中心天体最近的点(轨道的最低点),'''apoapsis''' (<tt>Q</tt>) | + | :每个椭圆轨道都有两个拱点。'''periapsis''' (<tt>q</tt>)(近拱点)是距离轨道中心天体最近的点(轨道的最低点),'''apoapsis''' (<tt>Q</tt>) (远拱点)是另一侧距离轨道中心天体最远的点(轨道的最高点)。天体总是在椭圆的两个焦点之一上,远近拱点高度等于长轴两端到某一焦点的距离减去天体半径。 |
;近-* 和 远-* (peri-* and apo-*) | ;近-* 和 远-* (peri-* and apo-*) | ||
| Line 45: | Line 45: | ||
;<span id="an">升交点(ascending node)</span> | ;<span id="an">升交点(ascending node)</span> | ||
| − | : | + | :以中心天体为参考系,飞行器穿过赤道面,向“北极”运动的点。“北”向,是参考轨道中心天体的坐标系。 |
;降交点(descending node) | ;降交点(descending node) | ||
| − | : | + | :以中心天体为参考系,飞行器穿过赤道面,向“南极”运动的点。 |
;<span id="ecc">离心率(eccentricity)</span> | ;<span id="ecc">离心率(eccentricity)</span> | ||
{{See also|Orbit|section=Eccentricity}} | {{See also|Orbit|section=Eccentricity}} | ||
| Line 60: | Line 60: | ||
:轨道平面与参考平面的夹角。(例如,90° 赤道平面倾角轨道就是所谓的极地轨道。) | :轨道平面与参考平面的夹角。(例如,90° 赤道平面倾角轨道就是所谓的极地轨道。) | ||
;<span id="lo">低轨道</span> | ;<span id="lo">低轨道</span> | ||
| − | : | + | : 这种轨道的高度刚好可以脱离环绕天体对于轨道的不利影响,如空气阻力。低轨道通常都作为后续机动的“停泊轨道”,位于上升段和向其他最终的目的地出发之间,在轨道的任意点都可以进行飞船脱离轨道的点火推进。其优点就是抵达低轨道所需要的燃料是最少的。环绕 [[Kerbin]] 的低轨道高度通常介于 70km 到 100km。理论上而言,对于没有大气层的天体,其低轨道只需高于地表,但考虑到地形碰撞的影响,一般都高于 10km。在低轨道只能选择小比率快进[[time warp]]。 |
| − | ;<span id="on"> | + | ;<span id="on">轨道节点</span> ''(天文学定义)'' |
| − | : | + | :飞行器穿过轨道平面的点。飞行器在升交点穿过参考轨道平面,向轨道平面的法线方向运动。 通常升交点指向北极,降交点(反法线方向)指向南极。 |
| − | ;<span id="node"> | + | ;<span id="node">轨道节点</span> ''(游戏中)'' |
:轨道中的特定点,如近点、远点,以及与其他轨道的交汇点等等。 | :轨道中的特定点,如近点、远点,以及与其他轨道的交汇点等等。 | ||
;轨道法向(orbit normal) | ;轨道法向(orbit normal) | ||
| Line 69: | Line 69: | ||
;轨道平面(orbital plane) | ;轨道平面(orbital plane) | ||
:描述轨道环绕飞行平面的虚拟圆盘(通常用于表述轨道倾角)。 | :描述轨道环绕飞行平面的虚拟圆盘(通常用于表述轨道倾角)。 | ||
| − | ;<span id="orbspeed"> | + | ;<span id="orbspeed">轨道速度</span> |
| − | : | + | :轨道速度指的是环绕一个大质量天体重力中心的飞行器速度,可以用来表示在一个天体周围建立一个完整轨道所需要的速度,或是飞行器在轨道上某一点的瞬时速度。 |
;<span id="prograde">顺行(prograde)</span> | ;<span id="prograde">顺行(prograde)</span> | ||
:轨道路径的前进方向。由于轨道为椭圆形,因此实际上它的方向是飞船所处轨道位置的切线方向。 | :轨道路径的前进方向。由于轨道为椭圆形,因此实际上它的方向是飞船所处轨道位置的切线方向。 | ||
| Line 80: | Line 80: | ||
<math class="float-right">\text{a} = \text{R} + \frac{Q+q}{2}</math> | <math class="float-right">\text{a} = \text{R} + \frac{Q+q}{2}</math> | ||
{{See also|Orbit|section=Semi-major axis}} | {{See also|Orbit|section=Semi-major axis}} | ||
| − | : | + | :长轴是过焦点与椭圆相交的线长,而半长轴就是椭圆长轴的一半。轨道运行体的半长轴就是其中心椭圆轨道(近点+天体半径)、(远点距离+天体半径)的平均值。由于轨道远近点都是相对于轨道中心物体表面的距离,因此需要在公式中加入其半径。半长轴相同的轨道运行周期相同,无论离心率如何。 |
| − | ;<span id="sidereal period"> | + | ;<span id="sidereal period">恒星年</span> |
| − | : | + | :恒星年是一个天体或者飞行器围绕恒星转动一周所用的时间。这个周期在惯性参考系下成立。(不考虑广义相对论和系统自身的转动) |
;亚轨道(sub-orbit) | ;亚轨道(sub-orbit) | ||
:亚轨道近点位于行星表面之下,亚轨道飞行最终会与该行星发生交会碰撞。 | :亚轨道近点位于行星表面之下,亚轨道飞行最终会与该行星发生交会碰撞。 | ||
| − | ;<span id="synodic period"> | + | ;<span id="synodic period">朔望周期</span> |
| − | : | + | :朔望周期是一个天体在同一位置重新出现的时间周期,通常和两个以上的天体相关。 例如从地球上观察反射太阳光的月球,显现出相同的形状所需的时间。 朔望周期是[[Mun|Mun]]两次与Kerbol–Kerbin连成线的时间间隔. 月球的朔望周期和轨道周期不一样,因为地球在围着太阳转。 |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
| − | == Ship Orientation == | + | == 飞行器姿态(Ship Orientation) == |
| − | + | 飞行器姿态用来描述一个特定飞行器的状态。 这些术语通常以驾驶舱作为观察中心 | |
| − | ;Zenith | + | ;姿态(Attitude) |
| − | : | + | :飞行器和飞行速度矢量方向的角度。 |
| − | ;Nadir | + | ;天顶(Zenith) |
| − | : | + | :从天体重心出发经过飞行器的矢量。代指飞行器的上方 |
| − | ;Port | + | ;天底(Nadir) |
| − | : | + | :从飞行器出发指向天体重心的矢量。代指飞行器的下方,天顶的反方向。 |
| − | ;Starboard | + | ;左舷(Port) |
| − | : | + | :飞行器左侧 |
| − | ;Front | + | ;右舷(Starboard) |
| − | : | + | :飞行器右侧 |
| − | ;Aft | + | ;前方(Front) |
| − | : | + | :飞行器前方通常指向速度的方向 |
| + | ;后方(Aft) | ||
| + | :前方的反方向 | ||
| − | == 太空机动 == | + | == 太空机动(Space Maneuvers) == |
;大气层制动(atmospheric braking) | ;大气层制动(atmospheric braking) | ||
:→ 全文: [[Aerobraking|空气制动]] | :→ 全文: [[Aerobraking|空气制动]] | ||
:降低轨道近点,使其进入行星的大气层。这种飞行方式可以利用空气阻力降低飞行器的速度。它可以用于再进入(参考下文),也可以应用于轨道的调整,同时节约燃料。 | :降低轨道近点,使其进入行星的大气层。这种飞行方式可以利用空气阻力降低飞行器的速度。它可以用于再进入(参考下文),也可以应用于轨道的调整,同时节约燃料。 | ||
| + | ;石头制动(Lithobraking) | ||
| + | {{See also||{{Wikipedia|Lithobraking}}}} | ||
| + | :类似于空气刹车的制动方式,只不过从空气换成了地面。用这个有点戏谑的词表示这种减速方式不是为了把东西摔的稀巴烂。 lithos'', 是 “rock” 或者 “stone”的意思. | ||
| + | ;<span id="atmospheric entry">大气再入</span> | ||
| + | {{Main article|Atmospheric entry}} | ||
| + | :运用空气阻力给飞行器减速,创造一条落地的轨道。当飞行器速度很大时,会产生大量的摩擦热,所以必须进行防热处理,防止飞行器“弹”回太空。再入(Re-entry)通常指通过大气再入回到Kerbin,大气再入是更广义的词; | ||
;点火(burn) | ;点火(burn) | ||
:点燃发动机,通常目的是进行轨道调整。 | :点燃发动机,通常目的是进行轨道调整。 | ||
;圆化调整(circularizing) | ;圆化调整(circularizing) | ||
:这种机动(发动机点火推进)的目的是把轨道的偏心率调整到近似于零。通常是在轨道近/远点打开发动机推力来实现。 | :这种机动(发动机点火推进)的目的是把轨道的偏心率调整到近似于零。通常是在轨道近/远点打开发动机推力来实现。 | ||
| + | ;引力弹弓(Gravity assist) | ||
| + | :飞行器通过天体的双曲线轨道,和天体的引力势井作用,改变速度的大小和方向。飞行器速度大小增加,速度方向朝着天体运行方向改变。更大的天体质量和更低的近点(Pe)会造成更大的改变。(不撞上去) | ||
| + | ;捕获 | ||
| + | :进入一个天体的引力范围。 sphere of influence (SOI) | ||
| + | ;机动节点 | ||
| + | {{Main article|Maneuver node}} | ||
| + | :在大地图里计划一个机动,预测点火[[#burn|burn]]以后的新轨道,以便更好的执行机动。 | ||
| + | ;径向向内点火(Radial-in burn) | ||
| + | :一次向着天体重心的点火 (与法线(Normal)和顺行(Prograde)都垂直). 它会逆时针转动轨道,直到低点(Pe)穿过天体重心。与径向向外点火相反( radial-out burn) 这是返回地面最快的方式,但不是最有效率的。 | ||
| + | ;径向向外点火 | ||
| + | :一次向天体重心反方向的点火。它会顺时针转动轨道,直到低点(Pe)穿过天体重心。 与径向向内点火相反 | ||
;再入(re-entry) | ;再入(re-entry) | ||
| − | + | {{See also|#atmospheric entry|大气再入}} | |
;反向点火(retroburn) | ;反向点火(retroburn) | ||
:向飞船前进的反方向点火推进,例如,把发动机喷口转向顺行方向,飞船头部对准逆行方向。这是一个常用的机动,可以在不改变其他轨道参数的情况下降低轨道速度。 | :向飞船前进的反方向点火推进,例如,把发动机喷口转向顺行方向,飞船头部对准逆行方向。这是一个常用的机动,可以在不改变其他轨道参数的情况下降低轨道速度。 | ||
| Line 130: | Line 140: | ||
== 物理 == | == 物理 == | ||
| − | |||
;加速度(acceleration) | ;加速度(acceleration) | ||
| − | : | + | :速度的改变率(位移对于时间进行一阶求导得到了速度,二阶求导得到了加速度)。加速度是矢量,单位为“米/秒<sup>2</sup>”(m/s<sup>2</sup>). |
| − | ; | + | ;弹道轨迹(ballistic trajectory) |
| − | : | + | :普通下落物体的轨道为抛物线,一般的天体轨道为椭圆,逃逸轨道为双曲线。在火箭飞行中,它就是指飞行器只受重力影响,本身没有任何动力(如推力)的飞行轨道。 |
;速度改变量(Δv, delta-v) | ;速度改变量(Δv, delta-v) | ||
:飞行器速度的实际改变量或可能改变量。测量单位为米每秒(m/s)。质量增大在单位时间内会降低Δv,而增加推力可以在单位时间内提高Δv。这是一个有效计算推进效率的参量。例如,飞行器脱离Kerbin大气层并进入稳定轨道所需要的Δv大约是4,000 m/s。 | :飞行器速度的实际改变量或可能改变量。测量单位为米每秒(m/s)。质量增大在单位时间内会降低Δv,而增加推力可以在单位时间内提高Δv。这是一个有效计算推进效率的参量。例如,飞行器脱离Kerbin大气层并进入稳定轨道所需要的Δv大约是4,000 m/s。 | ||
| + | :定义为:<math>\Delta{v} = \int_{t_0}^{t_1} {\frac {|T|} {m}}\, dt</math> | ||
| + | :''T'' 是推力,''m'' 是实际的质量 | ||
| + | :无外力和方向变化时,其结果就是速度的变化: | ||
| + | : <math>\Delta{v} = \int_{t_0}^{t_1} {\frac {|T|} {m}}\ dt = \int_{t_0}^{t_1} {|a|}\ dt = | {v}_1 - {v}_0 |\,</math> | ||
| + | :如果以比冲计算的话: | ||
| + | : <math>\Delta{v} = | {v}_1 - {v}_0 |_{max}\ = -\int_{t_0}^{t_1} {I_{sp} \cdot g\ \cdot \frac{\dot{m}} {m}}\ dt = {I_{sp} \cdot g \cdot ln( \frac {m_0} {m_1})}\,</math> | ||
;能量(energy) | ;能量(energy) | ||
| − | :在轨飞行器的能量是其动能和势能之和。势能的计算公式是 <math>E_p = -\frac{G \cdot M \cdot m}{R}</math>,动能的计算公式是 <math>E_k = -\frac{1}{2} \cdot m \cdot v^2</math>,这里''G''是[[w:zh-cn:万有引力常数|万有引力常量]],''M''是行星的质量,''m''是飞行器的质量,''R''是距行星中心的距离,而''v'' | + | {{See also||{{Wikipedia|Specific orbital energy}}}} |
| + | :在轨飞行器的能量是其动能和势能之和。势能的计算公式是 <math>E_p = -\frac{G \cdot M \cdot m}{R}</math>,动能的计算公式是 <math>E_k = -\frac{1}{2} \cdot m \cdot v^2</math>,这里''G''是[[w:zh-cn:万有引力常数|万有引力常量]],''M''是行星的质量,''m''是飞行器的质量,''R''是距行星中心的距离,而''v''就是飞行器的速度。则在轨飞行器的能量计算公式就是<math>E = E_k + E_p = \frac{1}{2} m v^2 - \frac{G M m}{R}</math>。无推动时能量和保持不变:接近轨道近拱点时,势能转化为动能。而经过近拱点之后,动能就开始向势能转化。总能量大于零,飞行器就进入逃逸轨道。 | ||
| + | :KSP中圆锥曲线近似的模拟轨道,体现了开普勒定律的基本概念。 椭圆是平面上到两个固定点(焦点)的距离之和为常数的点之轨迹。 其中一个焦点是天体的重心。 当飞行器向天体移动,飞行器的重力势能向动能转化。如果轨道是椭圆,当飞行器远离天体向另一个焦点移动,动能向重力势能转化。如果飞行器在两个焦点之间直线移动,远/近点刚好和两个焦点重合。在一个焦点上,重力势能为0,另一个焦点上动能为0。如果轨道正好是圆形,轨道上每一点都是远/近点. | ||
| + | :还有一个特殊的量表示轨道能量 (<math>\epsilon</math>) ,但不考虑飞行器质量: <math>E_p = \epsilon_p m</math>, <math>E_k = \epsilon_k m</math>, <math>E = \epsilon \, m = (\epsilon_k + \epsilon_p) m = -\frac{G M}{2 a}</math>.所有具有相同半长轴 (''a'')的轨道有相同的轨道能量。 | ||
;逃逸速度(escape velocity) | ;逃逸速度(escape velocity) | ||
:脱离行星引力范围所需要的速度,其计算公式为 <math>v_e = \sqrt{\frac{2GM}{r}}</math> ,G是[[w:zh-cn:万有引力常数|万有引力常量]],M是行星的质量,r是行星半径。 | :脱离行星引力范围所需要的速度,其计算公式为 <math>v_e = \sqrt{\frac{2GM}{r}}</math> ,G是[[w:zh-cn:万有引力常数|万有引力常量]],M是行星的质量,r是行星半径。 | ||
;g力(G-force) | ;g力(G-force) | ||
| − | :g力是一个加速度的量度,不过其考虑了重力的影响。地球海平面测量得到的重力加速度约为9.81 m/ | + | :g力是一个加速度的量度,不过其考虑了重力的影响。地球海平面测量得到的重力加速度约为9.81 m/s²,将此定义为1G。地球表面物体的加速度大约都是1G。如果某物体受到的加速度为2G,其重量增加一倍。在轨运行并关闭发动机的航天器处于自由落体状态,此时为0G。(严格来说他们还是受到了重力产生的加速度,只不过加速度是径向向内的,不过不计算在G力里。) |
;引力(gravity) | ;引力(gravity) | ||
| − | : | + | :以物体的引力质量为力荷的力。本身非常微弱,只是那些质量很高的物体才能产生明显的引力,如行星、月亮等。其大小与物体中心距离的平方呈反比。所以距离增加到原先的两倍,其引力会降低到1/2<sup>2</sup>=1/4。 |
;引力井(gravity wall) | ;引力井(gravity wall) | ||
| − | : | + | :行星引力的作用范围。实际上这个区域是无限延伸的,但是由于引力会随着距离的增大急剧降低,其范围只是引力明显起作用的区域。但是采用圆锥曲线近似模拟的KSP里没有模拟出多个天体之间引力势井的影响。 |
;[[Orbit/zh-cn|轨道(orbit)]] | ;[[Orbit/zh-cn|轨道(orbit)]] | ||
| − | : | + | :当某物体具有足够大的切线速度(而且其位于大气层之外,无明显的空气阻力减速时),它会绕行星运行,并且不会落向该行星,这个运动轨迹就是轨道。稳定的轨道都是椭圆形(偏心率在0和1之间,圆形轨道就是一个偏心率为零的椭圆轨道)。如果其切线速度大于逃逸速度,那么它的轨道就成为抛物线(偏心率正好为1)或双曲线轨道(偏心率大于1)。 |
;<span id="isp">比冲(specific impulse, I<sub>sp</sub>)</span> | ;<span id="isp">比冲(specific impulse, I<sub>sp</sub>)</span> | ||
:<math style="float:right">I_{sp}= \frac{T}{\dot m}, [I_{sp}] = \frac{m}{s}</math>比冲 I<sub>sp</sub> 是对一个推进系统的燃烧效率的描述。比冲越高,单位燃料所产生的推力越大。通常比冲的单位可以用''秒''来表示,不过其正确的物理学单位为 ''距离每单位时间'',通常用 ''米每秒'' 或 ''英尺每秒''。为避免与速度的单位混淆,物理学上会把比冲除以地球(或Kerbin)表面的重力加速度(9.81 m/s²)再使用。这样比冲的单位就是''秒''。在公式中实际使用比冲时,它必须转化为正确的物理学单位——''距离每单位时间'',即再乘以地球(或Kerbin)表面的重力加速度(9.81 m/s²)。这种比冲值只是为了单位的转换,'''比冲并不随引力的变化而变化'''。 | :<math style="float:right">I_{sp}= \frac{T}{\dot m}, [I_{sp}] = \frac{m}{s}</math>比冲 I<sub>sp</sub> 是对一个推进系统的燃烧效率的描述。比冲越高,单位燃料所产生的推力越大。通常比冲的单位可以用''秒''来表示,不过其正确的物理学单位为 ''距离每单位时间'',通常用 ''米每秒'' 或 ''英尺每秒''。为避免与速度的单位混淆,物理学上会把比冲除以地球(或Kerbin)表面的重力加速度(9.81 m/s²)再使用。这样比冲的单位就是''秒''。在公式中实际使用比冲时,它必须转化为正确的物理学单位——''距离每单位时间'',即再乘以地球(或Kerbin)表面的重力加速度(9.81 m/s²)。这种比冲值只是为了单位的转换,'''比冲并不随引力的变化而变化'''。 | ||
| Line 156: | Line 174: | ||
;切向速度(tangential velocity) | ;切向速度(tangential velocity) | ||
:物体沿其飞行轨迹切线方向的速度分量。瞬时速度的方向永远是运动轨迹的切线方向。 | :物体沿其飞行轨迹切线方向的速度分量。瞬时速度的方向永远是运动轨迹的切线方向。 | ||
| + | ;<span id="TWR">推重比(thrust-weight-ratio, TWR)</span> | ||
| + | {{See also|Thrust-to-weight ratio}} | ||
| + | :<math style="float:right;padding:.5em;">\text{TWR} = \frac{T}{W} = \frac{T}{m \cdot g}</math>飞船总质量与动力段所有发动机总推力的比值。若TWR>1,飞船可以完成加速和上升。若TWR<1,飞船是无法克服重力和低飞行高度空气阻力的,不过低 TWR 在太空或许可以足够保证飞行器的运动。因为飞船重量(W)与其所处位置的重力加速度(g)成正比,TWR也跟具体位置有关。[[Mün]]表面的重力加速度只是Kerbin表面重力加速度的16.6%,因此,TWR<sub>Kerbin</sub> = 1相当于TWR<sub>Mün</sub> = 6。 | ||
;轨迹(trajectory) | ;轨迹(trajectory) | ||
:轨迹是运动物体以时间为变量所得到的空间位置所组成的路径。 | :轨迹是运动物体以时间为变量所得到的空间位置所组成的路径。 | ||
| Line 164: | Line 185: | ||
* [[Tutorials/zh-cn|教程]] | * [[Tutorials/zh-cn|教程]] | ||
* [[Acronyms and Initialisms|缩略词]] | * [[Acronyms and Initialisms|缩略词]] | ||
| − | * [[Deep Space Kraken]] | + | * [[Deep Space Kraken|深空海妖(en)]] |
Latest revision as of 05:39, 30 May 2022
KSP中使用了大量物理学和轨道飞行的术语,面对这些词语时,非专业人员无疑是会异常困惑,更不要说还有大量的其他科学词汇和缩写了。
本页就是一个相关术语简洁的查询表单,希望能帮助你顺利的走上专业宇航员之路。
Contents
[hide]数学
- 椭圆(Elliptical)
- 椭圆形,环绕轨道的常见状态。
- 双曲线(Hyperbolic)
- 开放的光滑曲线,通常对应的是逃逸轨道。
- 法向量(Normal Vector)
- 一条与平面垂直的向量。(在赤道轨道上,法向量指向北极的方向)
- 标量(scalar)
- 一个没有方向的数值。标量一般会有测量单位的后缀,表明这个标量的量纲。 比如 3 米每秒(m/s), 3 米(m),3 秒(s) 都是标量:它们分别是速率(区分于速度)、路程(区分于位移)和时间的单位,但不含方向。
- 向量, 矢量(vector)
- 一个方向和大小的集合。比如前进方向和速率放在一起就是速度。一个向量如何被表示取决于采用的坐标系,以及多少个维度被使用。 <35°, 12>是一个二维的极坐标向量,而<14, 9, -20>则是一个三维笛卡尔(直角)坐标向量。也有其他的坐标系,但这些是最常用的。
- <35°, 12>是一个12个单位长的箭头,从原点(零点,角度在这里没有意义,因为这是一个没有长度的点)出发,结束在一个与偏离极轴(通常是x轴,逆时针旋转为正角度)35°的点。
- <14, 9, -20>是一个从原点(<0,0,0>)出发,在一个x坐标为14,y坐标为9,z坐标为20的点终止的箭头。
- 使用直角坐标系的优点是你可以准确地知道向量的终止位置在哪里,但是计算向量的长度则比较麻烦。而在极坐标系中,向量长度十分易得,终止位置却较难得出。
- 速度、加速度、力、动量等物理量都是矢量。
一个三维坐标系需要:
- 一个参考系原点。
- 3个单位向量。这些向量定义了沿着坐标轴的基本量度和坐标轴的方向。
- 3个标量,这可以是角度或坐标,用来描述坐标空间中的位置。
轨道
- 轨道远拱点(apoapsis)
- 轨道近拱点(periapsis)
- 拱点
- → See also: “Apoapsis and periapsis” section in Orbit
- 每个椭圆轨道都有两个拱点。periapsis (q)(近拱点)是距离轨道中心天体最近的点(轨道的最低点),apoapsis (Q) (远拱点)是另一侧距离轨道中心天体最远的点(轨道的最高点)。天体总是在椭圆的两个焦点之一上,远近拱点高度等于长轴两端到某一焦点的距离减去天体半径。
- 近-* 和 远-* (peri-* and apo-*)
- 谈到轨道,我们通常都用具体的天体名称来指明轨道中心。因此,在这个游戏中,对于环绕Kerbin的轨道,我们会用近Kerbin点(Perikee, Perikerb)、远Kerbin点(Apokee, Apokerb)这样的名称。
- 升交点(ascending node)
- 以中心天体为参考系,飞行器穿过赤道面,向“北极”运动的点。“北”向,是参考轨道中心天体的坐标系。
- 降交点(descending node)
- 以中心天体为参考系,飞行器穿过赤道面,向“南极”运动的点。
- 离心率(eccentricity)
- → See also: “Eccentricity” section in Orbit
- 描述轨道近圆几何特征的参数。
- ecc = 0 → 圆形轨道;
- 0 < ecc < 1 → 椭圆轨道;
- ecc = 1 → 抛物线轨道 - 这是一种逃逸轨道;
- ecc > 1 → 双曲线轨道 - 这是另一种逃逸轨道;
- 轨道倾角(inclination)
- → See also: “Inclination” section in Orbit
- 轨道平面与参考平面的夹角。(例如,90° 赤道平面倾角轨道就是所谓的极地轨道。)
- 低轨道
- 这种轨道的高度刚好可以脱离环绕天体对于轨道的不利影响,如空气阻力。低轨道通常都作为后续机动的“停泊轨道”,位于上升段和向其他最终的目的地出发之间,在轨道的任意点都可以进行飞船脱离轨道的点火推进。其优点就是抵达低轨道所需要的燃料是最少的。环绕 Kerbin 的低轨道高度通常介于 70km 到 100km。理论上而言,对于没有大气层的天体,其低轨道只需高于地表,但考虑到地形碰撞的影响,一般都高于 10km。在低轨道只能选择小比率快进time warp。
- 轨道节点 (天文学定义)
- 飞行器穿过轨道平面的点。飞行器在升交点穿过参考轨道平面,向轨道平面的法线方向运动。 通常升交点指向北极,降交点(反法线方向)指向南极。
- 轨道节点 (游戏中)
- 轨道中的特定点,如近点、远点,以及与其他轨道的交汇点等等。
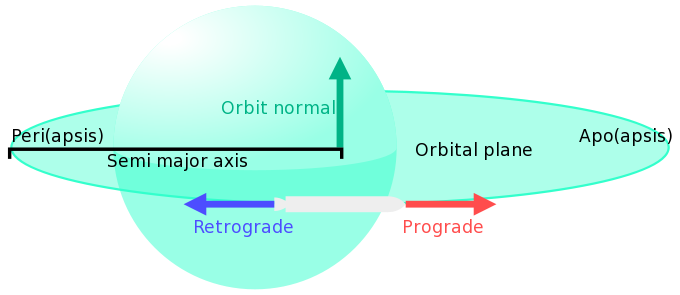
- 轨道法向(orbit normal)
- 轨道平面的正交方向矢量。飞船速度矢量方向与重力矢量方向的矢量和就是轨道法向。其遵照右手规则,飞船在轨道逆时针飞行时,其轨道法向朝“上”,顺时针则朝下。而“上”也就是“北”,或“N+”,“下”也叫做“逆法向”,“南”或者 “N-”。
- 轨道平面(orbital plane)
- 描述轨道环绕飞行平面的虚拟圆盘(通常用于表述轨道倾角)。
- 轨道速度
- 轨道速度指的是环绕一个大质量天体重力中心的飞行器速度,可以用来表示在一个天体周围建立一个完整轨道所需要的速度,或是飞行器在轨道上某一点的瞬时速度。
- 顺行(prograde)
- 轨道路径的前进方向。由于轨道为椭圆形,因此实际上它的方向是飞船所处轨道位置的切线方向。
- 逆行(retrograde)
- 顺行的反向。
- 参考平面(reference plane)
- 所有飞行器在描述其所处轨道时都需要一个参考平面。对于行星轨道,通常是采用其赤道平面作为参照。类似太阳系的多天体平面为参考时,以黄道平面作为参考平面。在以其他轨道为目标飞行时,应采用目标轨道平面。轨道偏心率和上升点经度(以参考平面为坐标系)即可确定轨道平面。
- 半长轴(semi-major axis)
- → See also: “Semi-major axis” section in Orbit
- 长轴是过焦点与椭圆相交的线长,而半长轴就是椭圆长轴的一半。轨道运行体的半长轴就是其中心椭圆轨道(近点+天体半径)、(远点距离+天体半径)的平均值。由于轨道远近点都是相对于轨道中心物体表面的距离,因此需要在公式中加入其半径。半长轴相同的轨道运行周期相同,无论离心率如何。
- 恒星年
- 恒星年是一个天体或者飞行器围绕恒星转动一周所用的时间。这个周期在惯性参考系下成立。(不考虑广义相对论和系统自身的转动)
- 亚轨道(sub-orbit)
- 亚轨道近点位于行星表面之下,亚轨道飞行最终会与该行星发生交会碰撞。
- 朔望周期
- 朔望周期是一个天体在同一位置重新出现的时间周期,通常和两个以上的天体相关。 例如从地球上观察反射太阳光的月球,显现出相同的形状所需的时间。 朔望周期是Mun两次与Kerbol–Kerbin连成线的时间间隔. 月球的朔望周期和轨道周期不一样,因为地球在围着太阳转。
飞行器姿态(Ship Orientation)
飞行器姿态用来描述一个特定飞行器的状态。 这些术语通常以驾驶舱作为观察中心
- 姿态(Attitude)
- 飞行器和飞行速度矢量方向的角度。
- 天顶(Zenith)
- 从天体重心出发经过飞行器的矢量。代指飞行器的上方
- 天底(Nadir)
- 从飞行器出发指向天体重心的矢量。代指飞行器的下方,天顶的反方向。
- 左舷(Port)
- 飞行器左侧
- 右舷(Starboard)
- 飞行器右侧
- 前方(Front)
- 飞行器前方通常指向速度的方向
- 后方(Aft)
- 前方的反方向
太空机动(Space Maneuvers)
- 大气层制动(atmospheric braking)
- → 全文: 空气制动
- 降低轨道近点,使其进入行星的大气层。这种飞行方式可以利用空气阻力降低飞行器的速度。它可以用于再进入(参考下文),也可以应用于轨道的调整,同时节约燃料。
- 石头制动(Lithobraking)
- → See also: Lithobraking on Wikipedia
- 类似于空气刹车的制动方式,只不过从空气换成了地面。用这个有点戏谑的词表示这种减速方式不是为了把东西摔的稀巴烂。 lithos, 是 “rock” 或者 “stone”的意思.
- 大气再入
- → Main article: Atmospheric entry
- 运用空气阻力给飞行器减速,创造一条落地的轨道。当飞行器速度很大时,会产生大量的摩擦热,所以必须进行防热处理,防止飞行器“弹”回太空。再入(Re-entry)通常指通过大气再入回到Kerbin,大气再入是更广义的词;
- 点火(burn)
- 点燃发动机,通常目的是进行轨道调整。
- 圆化调整(circularizing)
- 这种机动(发动机点火推进)的目的是把轨道的偏心率调整到近似于零。通常是在轨道近/远点打开发动机推力来实现。
- 引力弹弓(Gravity assist)
- 飞行器通过天体的双曲线轨道,和天体的引力势井作用,改变速度的大小和方向。飞行器速度大小增加,速度方向朝着天体运行方向改变。更大的天体质量和更低的近点(Pe)会造成更大的改变。(不撞上去)
- 捕获
- 进入一个天体的引力范围。 sphere of influence (SOI)
- 机动节点
- → Main article: Maneuver node
- 在大地图里计划一个机动,预测点火burn以后的新轨道,以便更好的执行机动。
- 径向向内点火(Radial-in burn)
- 一次向着天体重心的点火 (与法线(Normal)和顺行(Prograde)都垂直). 它会逆时针转动轨道,直到低点(Pe)穿过天体重心。与径向向外点火相反( radial-out burn) 这是返回地面最快的方式,但不是最有效率的。
- 径向向外点火
- 一次向天体重心反方向的点火。它会顺时针转动轨道,直到低点(Pe)穿过天体重心。 与径向向内点火相反
- 再入(re-entry)
- → See also: 大气再入
- 反向点火(retroburn)
- 向飞船前进的反方向点火推进,例如,把发动机喷口转向顺行方向,飞船头部对准逆行方向。这是一个常用的机动,可以在不改变其他轨道参数的情况下降低轨道速度。
物理
- 加速度(acceleration)
- 速度的改变率(位移对于时间进行一阶求导得到了速度,二阶求导得到了加速度)。加速度是矢量,单位为“米/秒2”(m/s2).
- 弹道轨迹(ballistic trajectory)
- 普通下落物体的轨道为抛物线,一般的天体轨道为椭圆,逃逸轨道为双曲线。在火箭飞行中,它就是指飞行器只受重力影响,本身没有任何动力(如推力)的飞行轨道。
- 速度改变量(Δv, delta-v)
- 飞行器速度的实际改变量或可能改变量。测量单位为米每秒(m/s)。质量增大在单位时间内会降低Δv,而增加推力可以在单位时间内提高Δv。这是一个有效计算推进效率的参量。例如,飞行器脱离Kerbin大气层并进入稳定轨道所需要的Δv大约是4,000 m/s。
- 定义为:
- T 是推力,m 是实际的质量
- 无外力和方向变化时,其结果就是速度的变化:
- 如果以比冲计算的话:
- 能量(energy)
- → See also: Specific orbital energy on Wikipedia
- 在轨飞行器的能量是其动能和势能之和。势能的计算公式是 ,动能的计算公式是 ,这里G是万有引力常量,M是行星的质量,m是飞行器的质量,R是距行星中心的距离,而v就是飞行器的速度。则在轨飞行器的能量计算公式就是。无推动时能量和保持不变:接近轨道近拱点时,势能转化为动能。而经过近拱点之后,动能就开始向势能转化。总能量大于零,飞行器就进入逃逸轨道。
- KSP中圆锥曲线近似的模拟轨道,体现了开普勒定律的基本概念。 椭圆是平面上到两个固定点(焦点)的距离之和为常数的点之轨迹。 其中一个焦点是天体的重心。 当飞行器向天体移动,飞行器的重力势能向动能转化。如果轨道是椭圆,当飞行器远离天体向另一个焦点移动,动能向重力势能转化。如果飞行器在两个焦点之间直线移动,远/近点刚好和两个焦点重合。在一个焦点上,重力势能为0,另一个焦点上动能为0。如果轨道正好是圆形,轨道上每一点都是远/近点.
- 还有一个特殊的量表示轨道能量 () ,但不考虑飞行器质量: , , .所有具有相同半长轴 (a)的轨道有相同的轨道能量。
- 逃逸速度(escape velocity)
- 脱离行星引力范围所需要的速度,其计算公式为 ,G是万有引力常量,M是行星的质量,r是行星半径。
- g力(G-force)
- g力是一个加速度的量度,不过其考虑了重力的影响。地球海平面测量得到的重力加速度约为9.81 m/s²,将此定义为1G。地球表面物体的加速度大约都是1G。如果某物体受到的加速度为2G,其重量增加一倍。在轨运行并关闭发动机的航天器处于自由落体状态,此时为0G。(严格来说他们还是受到了重力产生的加速度,只不过加速度是径向向内的,不过不计算在G力里。)
- 引力(gravity)
- 以物体的引力质量为力荷的力。本身非常微弱,只是那些质量很高的物体才能产生明显的引力,如行星、月亮等。其大小与物体中心距离的平方呈反比。所以距离增加到原先的两倍,其引力会降低到1/22=1/4。
- 引力井(gravity wall)
- 行星引力的作用范围。实际上这个区域是无限延伸的,但是由于引力会随着距离的增大急剧降低,其范围只是引力明显起作用的区域。但是采用圆锥曲线近似模拟的KSP里没有模拟出多个天体之间引力势井的影响。
- 轨道(orbit)
- 当某物体具有足够大的切线速度(而且其位于大气层之外,无明显的空气阻力减速时),它会绕行星运行,并且不会落向该行星,这个运动轨迹就是轨道。稳定的轨道都是椭圆形(偏心率在0和1之间,圆形轨道就是一个偏心率为零的椭圆轨道)。如果其切线速度大于逃逸速度,那么它的轨道就成为抛物线(偏心率正好为1)或双曲线轨道(偏心率大于1)。
- 比冲(specific impulse, Isp)
- 比冲 Isp 是对一个推进系统的燃烧效率的描述。比冲越高,单位燃料所产生的推力越大。通常比冲的单位可以用秒来表示,不过其正确的物理学单位为 距离每单位时间,通常用 米每秒 或 英尺每秒。为避免与速度的单位混淆,物理学上会把比冲除以地球(或Kerbin)表面的重力加速度(9.81 m/s²)再使用。这样比冲的单位就是秒。在公式中实际使用比冲时,它必须转化为正确的物理学单位——距离每单位时间,即再乘以地球(或Kerbin)表面的重力加速度(9.81 m/s²)。这种比冲值只是为了单位的转换,比冲并不随引力的变化而变化。
- 比冲是推力和燃料流量的比值,所以有时候会以作为其单位。这只是另一种数学形式, ,而力是质量和加速度之乘积,即,所以在国际单位制下可以得到 。
- 作用范围(sphere of influence, SoI, SOI)
- 以该天体为主要引力源的球体范围。游戏中在特定天体的作用范围内的飞船只考虑该天体的引力。
- 切向速度(tangential velocity)
- 物体沿其飞行轨迹切线方向的速度分量。瞬时速度的方向永远是运动轨迹的切线方向。
- 推重比(thrust-weight-ratio, TWR)
- → See also: Thrust-to-weight ratio
- 飞船总质量与动力段所有发动机总推力的比值。若TWR>1,飞船可以完成加速和上升。若TWR<1,飞船是无法克服重力和低飞行高度空气阻力的,不过低 TWR 在太空或许可以足够保证飞行器的运动。因为飞船重量(W)与其所处位置的重力加速度(g)成正比,TWR也跟具体位置有关。Mün表面的重力加速度只是Kerbin表面重力加速度的16.6%,因此,TWRKerbin = 1相当于TWRMün = 6。
- 轨迹(trajectory)
- 轨迹是运动物体以时间为变量所得到的空间位置所组成的路径。
- 速度(velocity)
- 位移随时间的变化率。速度是矢量,单位为米每秒(m/s)。
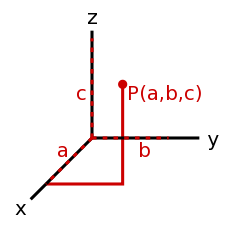
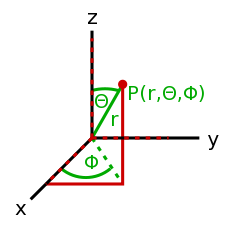













![I_{{sp}}={\frac {T}{{\dot m}}},[I_{{sp}}]={\frac {m}{s}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ff940eef93d9743a07d72ba2bb808e3b0372c36)




