Tutorial:Satellite Coverage

This tutorial is about how to calculate the satellite coverage of a celestial body. This is for example useful for RemoteTech. When placing multiple satellites in one orbit, it is more important that the semi-major axis is identical for all satellites. As long as the eccentricity is not very high it is more precise, than trying to make both apsides equal, and the orbital period only depends on the semi-major axis.

Distance between satellites

Illustrating the calculation

To determine the distance between two satellites if their angular distance is known can be calculated with following formula:

$l=2\cdot \sin \left({\frac {1}{2}}\alpha \right)\cdot (a+r)$

With $\alpha$ being the angular distance, $a$ the altitude above mean sea level and $r$ the radius of the orbited body. It is basically a isosceles triangle, where the base length is the distance between the satellites and the other both sides are from the center of mass of the orbited body to the satellites. For example two satellites at GSO around Kerbin with a distance of 90° are 4.9 Mm away. This calculation don't work, if the altitude of the two satellites isn't equal.

Satellite communication

Error creating thumbnail: /bin/bash: rsvg-convert: command not found

Six satellites in orbit around a celestial body in a regular polygon shape

The angular size β

Satellites are only able to communicate with each other, if both are in the line of sight. Depending on the number of satellites and altitude, it isn't always possible to communicate with the other satellites in the same orbit. To counteract this, either a higher orbit is chosen or more satellites are required. With the following formulas the altitude is linked with the number of satellites, so they determine at what altitude how many satellites are required to allow communication between them.

When all satellites in orbit have the same orbital period, the most efficient way to place them, is in the corners of a regular convex polygon. The interior angle of each point is then expressed with following formula:

$\alpha ={\frac {n-2}{n}}\cdot 180^{\circ }$

The next and previous satellite should have a angular distance of $\alpha$. Each satellite is placed on the same circular orbit and their position is a multiple of the following angle:

$\delta ={\frac {360^{\circ }}{n}}$

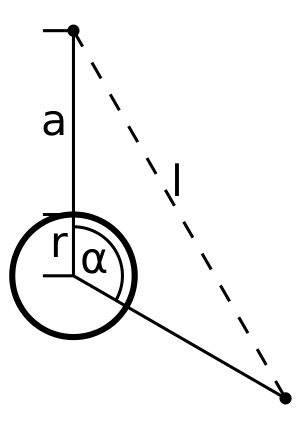
This means, that rotating the orbit with the value of $\delta$ the next and previous satellite are in the same spot than the observed one. Two satellites with a angular distance of $\delta$ need to be at least $\alpha$ degrees away. A celestial body with the radius of $r$ appears for a satellite with an altitude of $a$ above mean sea level of that body with this angular size:

$\beta =2\cdot \sin ^{-1}\left({\frac {r}{r+a}}\right)$

To have the next and previous satellites in sight the celestial body's size $\beta$ has to be lower than $\alpha$, so the other satellites appear above the horizon:

${\frac {n-2}{n}}\cdot 180^{\circ }=\left(1-{\frac {2}{n}}\right)\cdot 180^{\circ }=\alpha \geq \beta =2\cdot \sin ^{-1}\left({\frac {r}{r+a}}\right)$

The lowest altitude at which this is possible is when $\alpha =\beta$. Depending on what is given the following two equations are possible:

• There are n satellites and the minimum altitude a is required:

$a=\left({\frac {1}{\sin \left(\left(1-{\frac {2}{n}}\right)\cdot 90^{\circ }\right)}}-1\right)\cdot r$

• There is a desired altitude a and the required satellite count n is searched:

$n=-{\frac {2}{{\frac {1}{90^{\circ }}}\cdot \sin ^{-1}\left({\frac {r}{r+a}}\right)-1}}$

These calculations work only with at least three satellites.

Two satellite configuration

When using two satellites it is not possible to place them 180° apart, as they have no connection to each other than. So only two satellites can cover the complete celestial body. But when making the distance between both satellites as high as possible to 180°, it is possible to cover most of the body.