Terminology/hu
From Kerbal Space Program Wiki
A KSP-ben sok fizikára és pályák leírására vonatkozó kifejezés található, melyek zavaróak lehetnek a hozzá nem értőek számára, valamint egyéb változatos tudományos kifejezések és rövidítések melyekkel leírják a közkifejezéseket.
Ez a lap egy tömör szószedete a szükséges kifejezéseknek, mely segedelmével elindulhattok azon az úton amelyen zöldfülűekből képzett asztronautákká vagy rakétatudósokká válhattok! Mivel ez egy szószedet ezért a magyar kifejezés mellet megtalálhatjátok szögletes zárójelben a KSP világában található angol kifejezést is.
Contents
Matematika
- Elliptikus [Elliptical]
- Ovális-jellegű zárt pályagörbe, gyakran utalnak rá a pályák leírásakor.
- Normális avagy normál vektor [Normal vector]
- Egy az adott síkra merőleges egységvektor.
- Skalár [Scalar]
- Egy egyszerű érték irány nélkül. A skalárokat rendszerint a mértékegység követi, mely elárulja annak dimenzióját. Például 3 m/s, 3 m,3 s a "3" a skalár az utánuk következő mértékegységek elárulják, hogy sebesség, hossz/távolság vagy idő, de mindezt irány nélkül.
- Vektor [Vector]
- Irányok és értékek készlete. Például adott irányok és az arra mutató sebességkomponensek együtt megadják a sebességet. A vektor kifejezés függ a koordináta-rendszer fajtájától, valamint hogy mennyi dimenziót vettünk figyelembe. A <35°, 12> egy két dimenziós polár-vektor, míg a <14, 9, -20> egy háromdimenziós Descartes-féle derékszögű koordináta rendszerben értelmezhető vektor. 3 dimenzióban az előbb említett Descartes-féle derékszögű koordináta rendszer mellett gyakran alkalmazott - főleg egy bolygóhoz viszonyított helyzet megadására - a gömbi koordináta rendszer melyben két szög(szélesség, hosszúság) és a magasság adja meg a helyzetet amely egy 3 dimenziós polár koordináta-rendszer. Természetesen léteznek egyéb koordináta rendszerek, de ezek most számunkra lényegtelenek...
- <35°, 12> olyan mint egy 12 egység hosszú nyíl, amely az origóból indul ki és az alapvonallal bezáró 35°-os szög irányába mutat. Az alapvonal tipikusan az x-tengely és a szögeltolás az óramutatóval ellentétes irányba mutat.
- <14, 9, -20> olyan mint egy nyíl amelyik a kiindulási pontból(origóból)(<0,0,0>) kiindulva egy olyan pontban végződik amelynek az x koordinátája 14, az y koordinátája 9 és a z koordinátája -20.
- Descartes-féle derékszögű koordináta rendszer előnye, hogy pontosan megmutatja a végpont helyét, de nem ad közvetlen információt a vektor hosszáról, a polár koordináta rendszerben magától adódik a vektor hossza, de a végpont helyének meghatározása már nem olyan egyszerű.
- A következő fizikai mennyiségek mind vektorok: sebesség, gyorsulás, erő
Egy 3D koordináta rendszerhez az alábbiak kellenek:
- Egy referencia pont. Ez a kiindulási pont.
- 3 bázisvektorok. Ezek meghatározzák az alapértékét a tengelyirányú viszonyításnak és magát az adott tengelyt.
- Egy skalár hármas, amik lehetnek hosszak illetve szögek melyek meghatároznak egy helyet a koordináta rendszerben.
Pálya leíró kifejezések
- Apoapszis[Apoapsis]
- Periapszis[Periapsis]
- Apszis [Apsis]
- → Lásd még: “Apoapsis and periapsis” bekezdést a következő cikkből: Orbit
- Minden elliptikus pályának két apszisa van. A periapszis (q) a legközelebbi pontja a pályának (a legalacsonyabban ilyenkor van a keringő test) és az apoapszis (Q) amely a pálya túloldalán van és a legtávolabbi pont is egyben(a keringő test ilyenkor van a legmagasabban). Az apszisok értékeit gyakran az adott égitest felszínétől adják meg, miközben a legtöbb egyenlet számára a tömegközépponttól számított távolsággal dolgozik, így ilyenkor a felszíntől számított értékekhez hozzá kell adni a test sugarát.
- Peri-* és Apo-*
- Mikor pályákról beszélünk, gyakran a "periapszis" és "apoapszis" módosulnak a pálya közepén lévő égitest nevével. Például, -kee és -kerb mind gyakran használtak a Kerbin körüli pályák leírásakor, minek folytán Perikee/Perikerb és Apokee/Apokerb kifelyezésekkel is találkozhatunk.
- Felszálló csomó [Ascending node]
- Az a pont amelynél a pálya észak felé haladva metszi a referenciasíkot. Itt, "észak" a referenciasík normálisát jelenti.
- Leszálló csomó [Descending node]
- Az a pont ahol a a pálya délfelé haladva metszi a referencia síko.
- Excentricitás [Eccentricity]
- Egy skalár amely kifejezi a pálya körtől való eltérését .
- ecc = 0 → kör pálya.
- 0 < ecc < 1 → elliptikus pálya.
- ecc = 1 → parabolikus pálya - ez szökési pálya.
- ecc > 1 → hiperbolikus pálya - ez is szökési pálya.
- Inklínáció vagy pályahajlás [Inclination]
- A pályasík és a referenciasík által bezárt szög. (megjegyzés az egyenlítő síkjával 90°-ot bezáró pályát poláris-nak nevezik)
- Alacsony pálya [Low orbit]
- Egy stabil és biztonságos pálya amely csak éppen annyira magas, hogy elkerülje a veszélyeket, mint a légkörben való lefékeződést vagy éppen a hegyeknek való ütközést. Az alacsony pálya egy lépcsőfok amely a felemelkedés után várakozhatunk, hogy egy gyorsítással találkozhassunk egy másik járművel vagy égitesttel, vagy éppen az ellenkező irányban a legkevesebb üzemanyag felhasználásával szállhassunk le. A légkörrel rendelkező égitestek esetén, mint amilyen a Kerbin ez a közvetlenül a légkör feletti részt jelenti(70km-100km). A légkör nélküli égitesteknél ez elméletileg bármely felszin feletti magasság lehetne, de egy magasság alatt már a hegyek és magaslatok veszélyeztetik a pályát. Ilyenkor nem árt tudni a magaslatokról! Az időgyorsítás time warp nem korlátozva van az alacsony pályán, és lehetetlen az alatt.
- Pályacsomók [Orbital nodes]
- Bármely pályán lévő specifikus referenciapontok mint az Apoapszis, Periapszis, vagy a más pályákkal való metszéspontok[intersect points].
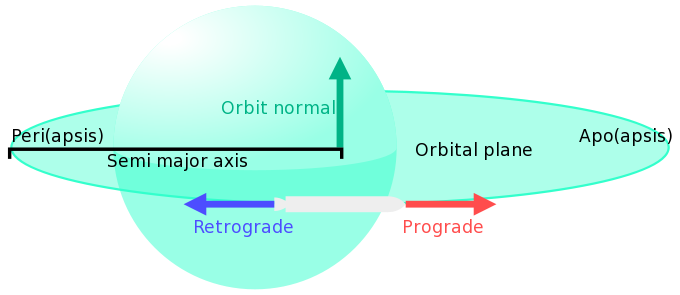
- Pályanormális [Orbit normal]
- A pályasík normálisa. Ezt a hajó sebessége és a gravitáció vektoriális szorzata adja. Mivel ez a jobbkéz szabályt követi, olyan nézőponból, ahonnan a hajó pozitív(az órajárással ellentétes) irányba kering felfelé(a szemlélő felé), ellenkező esetben pedig lefelé(a szelélőtől el) fog mutatni. A "Fel"["Up"] gyakran mint "észak"["North"] or "N+", és a párja mint "Le"["Down"] másként "Anti-Normál"["Anti-Normal"] avagy "Dél"["South"] vagy "N-" van jelölve.
- Pályasík [Orbital plane]
- Egy sík, melyet a keringés pályája feszít ki.
- Prográd [Prograde]
- Az az irány amely felé a test halad a pályája mentén. Elliptikus pálya esetén ez mindig a test tartozkodási helyén vett érintő iránya.
- Retrográd [Retrograde]
- A prográd ellentetje, háttal a pályán haladási iránnyal.
- Referenciasík [Reference plane]
- Bármely sík, amelyet az aktuális pálya leírásakor viszonyítási alapként felhasználunk. A bolygók körüli pályák esetén ez ttöbbnyire az egyenlítő síkja. Több test esetén az elipszis síkját használhatják. Egy másik keringő test befogása esetén a befogandó test pályasíkját használják. Egy pályasíkot teljesen leír egy referenciasikhoz viszonyított pályaelhajlás és a felszálló csomó hosszúsági szöge[longitude].
- Fél nagytengely [Semi-major axis]
- → Lásd még: “Semi-major axis” bekezdést a következő cikkből: Orbit
- A nagy tegely a hosszú tengelye az ellipszisnek a fél nagytegely(a) ennek a fele. It's the average of the apoapsis (Q) and periapsis (q) computed relative to the center of the body. As both are relative to the body's surface, the radius (R) must be added. All orbits with the same semi-major axis have the same period, regardless of their eccentricity.
- Sub-orbital
- Describes an orbit where the periapsis is below the surface of a planetary body. If a suborbital path is followed for too long the orbiter will collide with the body being orbited.
- Thrust-to-weight ratio
- → Lásd még: Thrust-to-weight ratio
- The Ratio between the total mass of the vehicle and the available thrust of all propulsion devices of the vehicle/current stage. A TWR greater than 1 means the craft will have enough thrust to accelerate vertically and gain altitude. A TWR below 1 means that the craft won't be able to counteract gravity and drag at low altitudes, although in space it only means that maneuvers will take longer. Because the weight (W) depends on the current gravitational acceleration (g) the TWR depends on which body is currently influencing the craft. The acceleration on the Mun's surface is only 16.6 % of Kerbin's acceleration, so at the surface a TWRKerbin = 1 would be a TWRMun = 6.
Ship Orientation
The ship orientation is always relative to a specific object. The terms are usually defined relative to the cockpit.
- Zenith
- Top side of the ship which is usually oriented away from the orbited body. Opposite of nadir.
- Nadir
- Bottom side of the ship which usually oriented towards the orbited body. Opposite of zenith.
- Port(side)
- Left side of the ship. Opposite of starboard.
- Starboard
- Right side of the ship. Opposite of portside.
- Front
- Front side/end of the ship which is usually towards the nose or prograde vector. Opposite of aft.
- Aft
- Back side/end of the ship which is usually housing the primary rockets and facing in retrograde. Opposite of front.
Space Maneuvers
- Atmospheric braking
- → Főcikk: Aerobraking
- Lowering the periapsis so it is inside a planetary atmosphere. This will lead to the vessel being slowed by atmospheric drag. Can lead to atmospheric entry, but also is used to reduce the necessary burn time for significant orbit alterations.
- Atmospheric entry
- → Főcikk: Atmospheric entry
- Entering atmosphere and using drag to decelerate a vessel to a groundwards trajectory. In real-world science this causes intense heat stress on the object as the vessel requires sufficient speed to not "bounce" back from the atmosphere into space. Currently (0.23[outdated]) atmospheric entry is only partially implemented with effects but heat and bounce are not yet implemented, there are mods however which allow parts to overheat. This is usually called re-entry/reentry but in theory only correct in Kerbin's atmosphere; atmospheric entry being the more general term.
- Burn
- firing of the engines, usually to alter trajectory in some way.
- Circularizing
- A maneuver (firing of the engines) that makes an orbit's eccentricity 0, or close to zero. This is usually achieved by a burn close to an apsis.
- Maneuver node
- → Főcikk: Maneuver node
- Maneuver nodes are a nice tool to plan and project trajectory changes in map view prior to doing the actual burn.
- Re-entry
- → Lásd még: Atmospheric entry
- Retroburn
- A burn performed "backwards", e.g. with the engines facing towards prograde and nose towards retrogade (hence the name). This is a common maneuver to used to lower the height of the orbit without altering any other orbital parameters.
Physics
- Acceleration
- Rate of change to the velocity. Acceleration is a vector, measured in "m/s2".
- Ballistic trajectory
- A falling object's trajectory is ballistic. In rocketry it usually indicates that the object in question is only influenced by gravity and does not exert any force (ie. thrust) of its own.
- Delta-v (Δv)
- The change in velocity that has or can be exerted by the spacecraft. This is measured in meters per second (m/s). More mass can reduce the delta-v, while more propulsion can increase it. This makes it a useful value to calculate the effectiveness of launch vehicles. For example, a launch vehicle requires about 4,500 m/s of delta-v to escape Kerbin's atmosphere and achieve a stable orbit.
- Energy
- → Lásd még: Specific orbital energy on Wikipedia
- The energy of an object in an orbit is the sum of its potential and kinetic energy. The potential energy is and kinetic energy where G is the gravitational constant, M is the mass of the body, m is the mass of the craft, R is the distance from the center of the body and v is the velocity. This results in . This sum stays the same when not thrusting: When approaching periapsis potential energy is transferred into kinetic energy. After passing the periapsis the kinetic energy is converted back into potential energy. When the energy or specific orbital energy is greater than zero the vehicle is on an escape trajectory.
- This is the basic idea behind Kepler's laws of planetary motion, which is what gives rise to KSP's patched conics approximation. An ellipse is the set of all points on a plane such that the sum of the distances to two points - the foci - is some constant. One focus of a Kepler orbit is the centre of mass of the object being orbited; as an object approaches it, it exchanges potential energy for kinetic energy. As the object moves away from this focus - equivalently, if the orbit is elliptical, as the object approaches the other focus - it exchanges kinetic energy for potential energy. If the craft going directly towards or away from the object, the foci coincide with the apsides, where the kinetic (apoapsis) or potential (periapsis) energy is zero. If it's perfectly circular (e.g. the Mun's orbit around Kerbin), the two foci coincide and the locations of the apsides are undefined, since every point of the orbit is an apsis.
- There is also the specific orbital energy () which doesn't require the mass of the craft: , , . All orbits with the same semi-major axis (a) have the same specific orbital energy.
- Escape Velocity
- The velocity needed to escape a given planet's gravity well, as given by where G is the gravitational constant, M is the mass of the planet, and r is the radius of the planet.
- g-force (G)
- A measurement of acceleration as expressed in the sea-level force of Earth's gravity with 1 G being about 9.81 m/s². An object at Earth's surface is accelerated at 1 G. The object weighs twice as much when at 2 G acceleration and is weightless when accelerated with 0 G. In free fall, like in orbit, and without an engine running or an atmosphere applying drag all objects experience no acceleration which can be expressed as 0 G.
- Gravity
- The force exerted by all objects with mass. Very weak. Usually only objects with very high mass - ie. planets, moons - have any noticeable effect. Diminishes with the square of distance from the center of mass. So for an object twice as far, experiences only 1/22 = 1/4 of the gravity.
- Gravity Well
- The area around a planet affected by gravity. Actually extends to infinity, but as gravity decreases quadratically with distance (after twice the distance the gravity is only a quarter), it is only significant within the body's sphere of influence. In fact, in KSP, gravity isn't simulated at all beyond a body's sphere of influence due to its use of the "patched conic approximation".
- Orbit
- → Főcikk: Orbit
- When an object has sufficient tangential velocity (and is outside the atmosphere, so drag won't slow it down) so that it will keep falling "next" to the planet (never touching ground) its trajectory is called an orbit. Stable orbits are elliptical (a circle is an ellipse with zero eccentricity). If the objects tangential speed exceeds escape velocity it's orbit will be either para- or hyperbolic.
- Specific Impulse (Isp)
- → Főcikk: Specific impulse
- The Isp defines how effective a propulsion system is. The higher the Isp the more powerful is the thrust applied to the rocket with the same fuel mass. The Isp is usually given in seconds but actually the physically correct unit is distance per time which is usually given in meters per second or feet per second. To avoid confusion which unit of speed is used, the physical correct Isp (in distance/time) is divided by the surface gravity of Earth (9.81 m/s²). This results in a value given in seconds. To use this Isp in formulas it must to be converted back into distance per time which requires multiplying with the surface gravity of Earth again. As this value is only used to convert between those two units, the specific impulse doesn't change when the gravity changes. It appears that KSP use a value like 9.82 m/s² and thus using a little less fuel.
- As the specific impulse is the ratio of thrust and fuel flow is sometimes given as the unit. This is mathematically another form of because force is the multiplication of mass and acceleration defining . So with the latter being simply only in SI base units.
- Sphere of influence
- → Főcikk: Sphere of influence
- The radius around a celestial body within which its gravity well is non-negligible. Commonly known as SoI/SOI.
- Tangential velocity
- The component of the velocity that is tangential to the trajectory. Instantaneous velocity - velocity when the time of measurement approaches zero - is always tangential to the trajectory.
- Trajectory
- A trajectory is the path that a moving object follows through space as a function of time.
- Velocity
- Rate of change of the position. It is the combination of speed with the direction. Velocity is a vector, measured in meters per second (m/s).
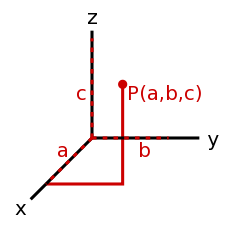
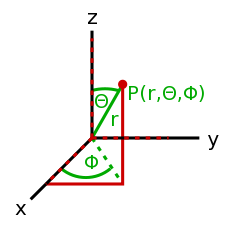











![I_{{sp}}={\frac {T}{{\dot m}}},[I_{{sp}}]={\frac {m}{s}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ff940eef93d9743a07d72ba2bb808e3b0372c36)



