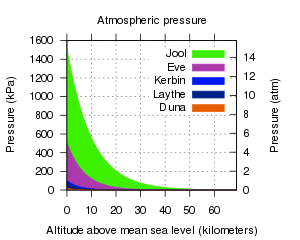
天体的 大气层 会让任何穿过它的物体的移动速度减低,因为有一种力叫做大气阻力(通常叫做“阻力”)。大气层通常可以进行气动飞升。含有大气层的天体有Eve,Kerbin,Duna以及Jool,还有Laythe,Jool的其中一个卫星。只有Kerbin和Laythe的大气层才有氧气,使得飞机引擎可以进气用以运作。
大气压力会随着海拔高度的增加而减少。一个大气层的缩放高度指的是通过其大气压力改变的因素e,或2.718。例如,柯尔滨的大气层拥有缩放高度为5800米,这就意味着在高度n上的大气压力比处于n + 5800 米处高了 2.718 倍。
尽管在游戏中没有相关表示,但是大气层中的温度不尽相同。
大气层可以进行大气制动并且着陆更简单。但是,大气层也会使离开一个行星变得更加困难,而且会增加其最低稳定轨道的高度。
阻力

一个因Kerbin大气层的阻力而减慢的装有 Mk16-XL 降落伞的 Mk1-2驾驶舱。
在游戏中,大气阻力所产生的力(FD)是这样计算的:[1]
-

其中ρ表示大气密度(千克/立方米),v表示飞船速度(米/秒)d表示阻力系数(无量纲),以及A表示截面积(平方米)。
注意这里的截面积并没有在游戏中实际参与运算,代替它的是由KSP按照质量比例直接计算的简化的不真实的假定值。FlightGlobals参数。阻力倍增说明了比例的比率为0.008平米/千克,因此:
-

其中m表示飞船质量(千克)。
大气密度ρ与大气压力直接相关(单位大气压的p),这里是一个关于在高度为0下的大气压力(p0)以及缩放高度(H)的函数:
-

其中 p 的单位是 大气压,ρ的单位是千克/立方米。1.2230948554874 是由FlightGlobals.getAtmDensity(1.0)所决定的,它所返回的是 1 个标准大气(Kerbin的海平面)压。
阻力系数(d)是由飞船上部件的max_drag(最大阻力)值的质量加权平均值所决定的。对于大多数没有降落伞的飞船来说,d的值都非常接近于0.2,因为这是绝大多数部件的max_drag值。并且一组同样的组件将会产生同样的阻力系数。
举个例子,一个由Mk1-2命令舱(质量4,阻力0.2)和一个展开的Mk16-XL 降落伞(质量0.3,阻力500)组成的飞船的阻力系数为:
-

终端速度
一个穿过大气层的物体的终端速度为使地心引力与阻力相等的速度。终端速度会因为一个高度函数而改变。给予足够的时间,一个掉进大气层的物体就会减速到终端速度然后会停留在终端速度上来短暂的停留。
终端速度很重要,因为:
- 它表示了一个飞行器必须在接近地表的位置开始燃烧。
- 它代表着一个飞行器可以以最省燃料的方式向上行进的速度。
地心引力(FG)为:
-

其中 m 仍然表示飞船的质量,G 表示引力常数, M 表示星球重量,R 和 r 代表着从行星中心到坠落物之间的距离。
为了找到终端速度,我们让 FG 等于 FD:
-

设 d 为 0.2(假定是一个没有使用降落伞的飞行器),它将被简化为:
-

使用上述中 Mk1-2 命令舱和 Mk16XL 降落伞的例子,阻力系数为 35.07,所以它在柯尔滨海平面(距离柯尔滨中心600千米)的终端速度为:
-

-

-

示例
| 海拔高度(米) |
vT(米/秒)
|
| Eve |
Kerbin |
Duna |
Jool |
Laythe
|
| 0 |
58.385 |
100.13 |
212.41 |
23.124 |
115.62
|
| 100 |
58.783 |
101.01 |
214.21 |
23.162 |
116.32
|
| 1000 |
62.494 |
109.30 |
231.16 |
23.508 |
122.83
|
| 10000 |
115.27 |
240.52 |
495.18 |
27.272 |
211.77
|
在轨物理
如果一艘飞船“在轨”(意思是它距离正在控制的飞船超过2.25千米)并且其轨道经过了一个星球的大气层,以下两件事将根据飞船高度的大气压力而发生其中之一:
- 低于 0.01大气压:不会遇到大气阻力 —— 飞船完全不会受到影响
- 0.01大气压或更高:飞船会消失
下表给出了每一种天体的大气层所对应的0.01大气压门槛高度:
大气层高度
大气层高度取决于天体的缩放高度,并且代表大气压力边缘的0.000001的(0.0001%)表面压力并不是常量。从技术上来讲,一个位于卓尔轨道上的航天器可以被其大气层(或者一个更高压力的大气层)拉低。


柯尔滨的大气层的末端位于0.000001 大气压处,下列算式用来计算其他天体的大气高度:

另见
注释
- ↑ http://forum.kerbalspaceprogram.com/showthread.php/5235-Atmospheric-drag?p=88804&viewfull=1#post88804