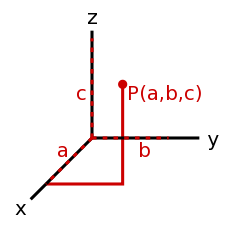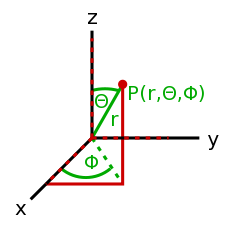Terminology/pl
From Kerbal Space Program Wiki
W KSP wykorzystywanych jest wiele słów odnoszących się do orbit i fizyki, które w swej zawiłości mogą być problematyczne dla "nietechnicznych". Dodatkowo mogą występować słowa i skróty, które w języku potocznym oznaczają co innego, niż w języku naukowym. Ta strona została stworzona, aby wyżej wymienione nieścisłości wyeliminować i pomóc czytelnikom wystartować na drodze do bycia opierzonym astronautą!
Matematyka
- Eliptyczne
- Owalne, często używane do opisu orbity.
- Hiperbloiczne
- Gładka krzywa, często używane do opisu trajektorii ucieczki.
- Skalar
- Warość bez kierunku. Przykładem skalara jest temperatura (np. 273,14 K), która nie ma kierunku, ani tym bardziej zwrotu.
- Wektor
- Zespół wartości określających pewną wielkość. Przykładem wektora jest prędkość obiektu zapisana w dwóch kierunkach. Rozpatrzmy przykład kulki rzucanej przy ścianie. Wpływ grawitacji pomijamy, czyli kulka nie spada, a cały czas leci przed siebie. Każdy rzut będzie wykonany z prędkością początkową 5 m/s. Wektor może mieć także zapis trój-, cztero-, pięcio- i wielowymiarowy (składać się z 3, 4, 5 lub wielu współrzędnych) oraz używać innego układu współrzędnych, np. polarnego.
- Wektor normalny
- Wektor prostopadły do wybranego obiektu. Wektor normalny do prostej będzie wyznaczał kierunek prostej prostopadłej do pierwszej prostej.
Nazewnictwo orbitalne
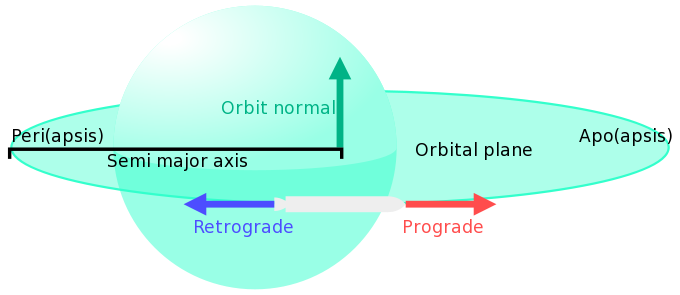
- Perycentrum i Apocetrum (Periapsis & Apoapsis)
- Każda eliptyczna orbita ma dwa centra. Perycentrum to punkt położony najbliżej orbitowanego ciała (najniższy punkt orbity). Apocentrum to analogicznie punkt położony najdalej od orbitowanego ciała (najwyższy punkt orbity). Centra są podawane z reguły w odniesieniu do powierzchni orbitowanego ciała, lecz większość równań potrzebuje odległości w odniesieniu do środka jego masy. W grze perycentrum nazwane jest "Periapsis", a apocentrum "Apoapsis".
- Pery-* i Apo-*
- Niekiedy słowo centrum w nazwach ekstremów zostanie zastąpione nazwą ciała orbitowanego. W niektórych artykułach można zatem spotkać nazwę perykerbin, perikerb lub perikee (artykuły anglojęzyczne).
- Punkt wznoszenia (Ascending node)
- Punkt na orbicie, w którym orbita przecina płaszczyznę odniesienia poruszając się na północ (zazwyczaj do góry).
- Punkt opadania (Descending node)
- Punkt na orbicie, w którym orbita przecina płaszczyznę odniesienia poruszając się na południe (zazwyczaj do dołu).
- Ekscentryczność
- Skalar opisujący poziom eliptyczności orbity.
- ecc = 0 → orbita kołowa
- 0 < ecc < 1 → orbita eliptyczna
- ecc = 1 → orbita paraboliczna (trajektoria ucieczki)
- ecc > 1 → orbita hiperboliczna (trajektoria ucieczki)
- Inklinacja
- Kąt pomiędzy powierzchnią orbity, a powierzchnią odniesienia. Inklinacja 90° oznacza orbitę polarną w odniesieniu do orbity równikowej.
- Niska orbita
- Najniższa orbita pozwalająca uniknąć przeszkód na ciele orbitowanym (np. atmosfera). Zazwyczaj niskie orbity są używane jako orbity parkingowe, na których statek może zaczekać na okno transferowe. Dla Kerbinu Niska Orbita Okołokerbinowa (ang. LKO - Low Kerbin Orbit) to minimum 70 km i rozciąga się do około 100 km. Teoretyczna wysokość niskiej orbity wokół ciał bez atmosfery to tuż nad powierzchnią, jednak poniżej 10 km ryzyko zderzenia z górami lub innymi wzniesieniami jest bardzo wysokie. Funkcja przyspieszenia czasu jest bardzo ograniczona na takich orbitach.
- Węzeł (Orbital node) - definicja astronomiczna
- Punkt na orbicie obiektu, w którym ciało przecina płaszczyznę odniesienia. Każda orbita ma dwa węzły.
- Węzły (Orbital nodes) - w grze
- Określone punkty dowolnej orbity, np. apocentrum, perycentrum, punkt wznoszenia, czy punkt opadania.
- Normalna orbity
- Wektor normalny do płaszczyzny orbity. Wynik mnożenia wektorów prędkości statku oraz grawitacji. Ponieważ działanie to odbywa się zgodnie z regułą śruby prawoskrętnej (znanej także jako reguła prawej ręki), to statek poruszający się normalna orbity statku poruszającego się przeciwnie do ruchu wskazówek zegara będzie skierowana "w górę", a poruszającego się zgodnie z ruchem wskazówek zegara - "w dół". "Góra" w tym wypadku może być oznaczana jako "północ", "N+", natomiast "Dół" "Anty normalną" ("Anti-Normal"), "południem", lub "N-".
- Płaszczyzna orbity
- Wirtualny dysk, na którego obrzeżach znajduje się orbita ciała.
- Prędkość orbitalna
- Prędkość, z jaką ciało orbitujące porusza się wokół centrum układu (zazwyczaj wokół bardziej masywnego ciała). Może oznaczać zarówno średnią prędkość, jak i prędkość chwilową.
- Przód (Prograde)
- Kierunek, w którym statek porusza się na orbicie. Ponieważ orbity są eliptyczne, kierunek ten jest zawsze styczny do miejsca na orbicie, w którym znajduje się statek.
- Tył (Retrograde)
- Kierunek przeciwny do przodu.
- Płaszczyzna odniesienia
- Dowolna płaszczyzna użyta jako "miejsce zero" do opisu pozycji statku. Dla orbit lokalnych wokół planet zazwyczaj używa się płaszczyzny wyznaczanej przez równik. Do manewrowania z innym statkiem zazwyczaj wykorzystuje się płaszczyznę utworzoną przez jego orbitę. Płaszczyzna orbity może być w pełni opisana poprzez inklinację i szerokość geograficzną punktu wzniesienia w oparciu o płaszczyznę odniesienia.