Difference between revisions of "Cheat sheet"

Revision as of 22:40, 10 June 2014 (view source) Mpink (talk | contribs) (Added Maximum DV Chart for single stage craft) ← Older edit		Revision as of 10:44, 11 June 2014 (view source) XZise (talk | contribs) m (→‎Maximum Δv Chart: +units;) Newer edit →
Line 65:		Line 65:
	{| class="wikitable"		{| class="wikitable"
	|-		|-
−	! ISP !! Max Δv !! Engines	+	! ISP (s) !! Max Δv (m/s) !! Engines
	|-		|-
	| 290 || 2762 || LV-1		| 290 || 2762 || LV-1

---

Revision as of 10:44, 11 June 2014

Kerbal Space Program rocket scientist's cheat sheet: Delta-v maps, equations and more for your reference so you can get from here to there and back again.

Mathematics

Thrust to Weight Ratio (TWR)

→ See also: Thrust-to-weight ratio

This is Newton's Second Law. If the ratio is less than 1 the craft will not lift off the ground. Note that the local gravitational acceleration, which is usually the surface gravity of the body the rocket is starting from, is required.

Combined Specific Impulse (I_sp)

→ See also: Specific impulse

If the I_sp is the same for all engines in a stage, then the I_sp is equal to a single engine. If the I_sp is different for engines in a single stage, then use the following equation:

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

Delta-v (Δv)

Basic calculation

→ See also: Tutorial:Advanced Rocket Design

Basic calculation of a rocket's Δv. Use the atmospheric and vacuum thrust values for atmospheric and vacuum Δv, respectively.

True Δv of a stage that crosses from atmosphere to vacuum

Body	Δvout
Kerbin	1000 m/s
other bodies' data missing

Calculation of a rocket stage's Δv, taking into account transitioning from atmosphere to vacuum. Δv_out is the amount of Δv required to leave a body's atmosphere, not reach orbit. This equation is useful to figure out the actual Δv of a stage that transitions from atmosphere to vacuum.

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}}$

Maps

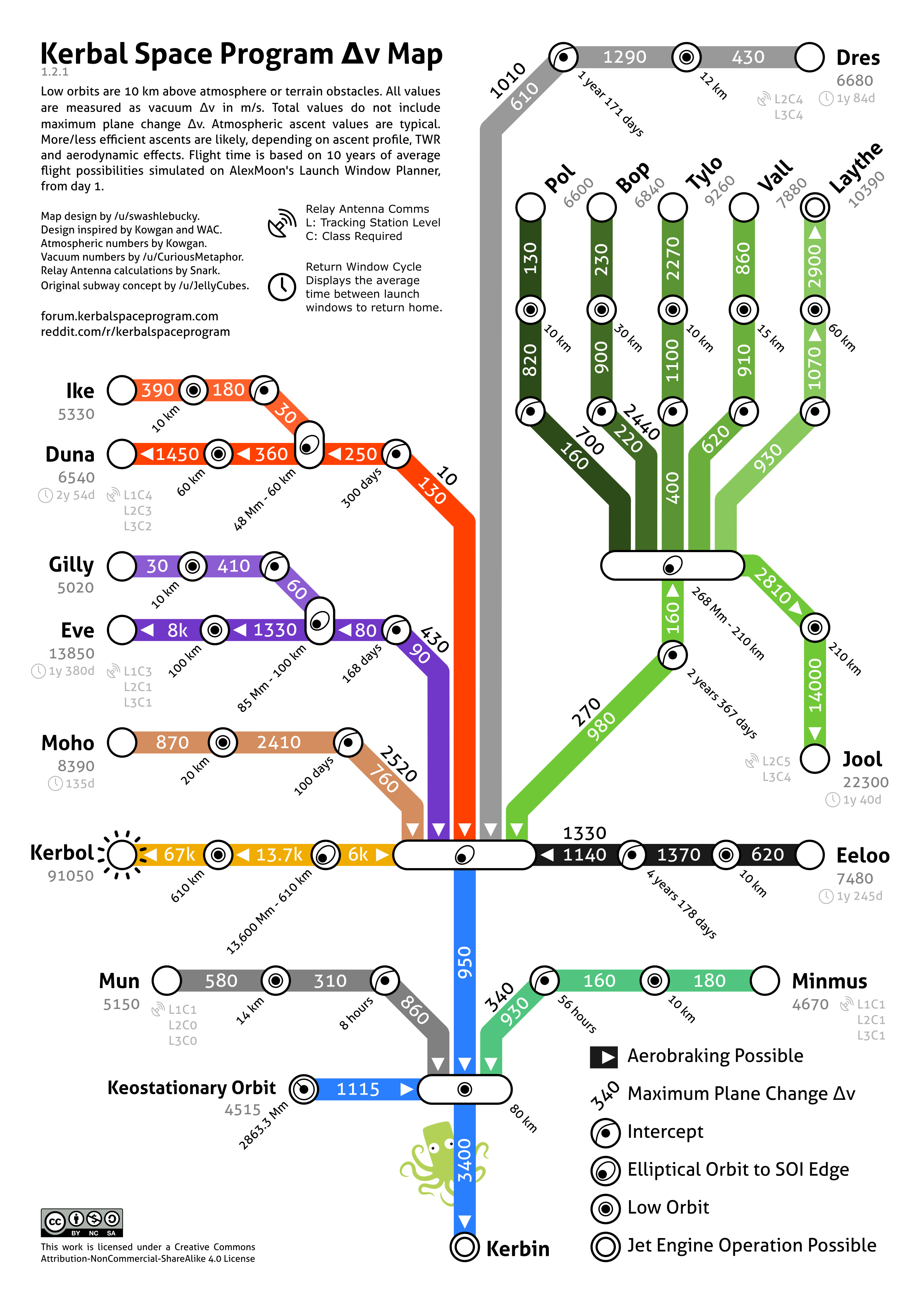
Various fan-made maps showing the Δv required to travel to a certain body.

Subway style Δv map:

Total Δv values

• http://www.skyrender.net/lp/ksp/system_map.png

Δv change values

• http://i.imgur.com/duY2S.png

Δv nomogram

• http://ubuntuone.com/1kD39BCoV38WP1QeG6MtO6

Δv with Phase Angles

• http://i.imgur.com/dXT6r7s.png

Precise Total Δv values

• http://i.imgur.com/UUU8yCk.png

Maximum Δv Chart

This table shows the Maximum Δv for a single stage craft using an engine of a given ISP fueled from the T-100 to Jumbo64 range operating in a vacuum. These Δv are not achievable as adding a payload (engine + command pod mass) and combined it with the exponential curve from the Δv calculation will prevent you from ever reaching it. It is however a good guide to what engine to use for a reusable interplanetary ship.

ISP (s)	Max Δv (m/s)	Engines
290	2762	LV-1 LV-1R
300	2857	Rockomax 24-77
320	3047	Mark-55
330	3143	Mainsail
350	3333	Skipper 48-7S
360	3428	KS-25X4 KR-1X2
370	3524	LV-T30 LV-T45
380	3619	KR-2L
390	3714	Poodle LV-909 Aerospike
800	7619	LV-N

Math examples

TWR

• Copy template:

TWR = F / (m * g) > 1

I_sp

1. When I_sp is the same for all engines in a stage, then the I_sp is equal to a single engine. So six 200 I_sp engines still yields only 200 I_sp.
2. When I_sp is different for engines in a single stage, then use the following equation:

• Equation:

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

• Simplified:

I_sp = ( F1 + F2 + ... ) / ( ( F1 / I_sp1 ) + ( F2 / I_sp2 ) + ... )

• Explained:

I_sp = ( Force of Thrust of 1st Engine + Force of Thrust of 2nd Engine...and so on... ) / ( ( Force of Thrust of 1st Engine / I_sp of 1st Engine ) + ( Force of Thrust of 2nd Engine / I_sp of 2nd Engine ) + ...and so on... )

• Example:

Two engines, one rated 200 newtons and 120 seconds I_sp ; another engine rated 50 newtons and 200 seconds I_sp.

Isp = (200 newtons + 50 newtons) / ( ( 200 newtons / 120 ) + ( 50 newtons / 200 ) = 130.89 seconds I_sp

Δv

1. For atmospheric Δv value, use atmospheric thrust values.
2. For vacuum Δv value, use vacuum thrust values.
3. Use this equation to figure out the Δv per stage:

• Equation:

${\displaystyle \Delta {v}=ln\left({\frac {M_{start}}{M_{dry}}}\right)\cdot I_{sp}\cdot 9.81{\frac {m}{s^{2}}}}$

• Simplified:

Δv = ln ( Mstart / Mdry ) * I_sp * g

• Explained:

Δv = ln ( Starting Mass / Dry Mass ) X Isp X 9.81

• Example:

Single Stage Rocket that weighs 23 tons when full, 15 tons when fuel is emptied, and engine that outputs 120 seconds I_sp.

Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds I_sp × 9.81m/s² = Total Δv of 503.2 m/s

True Δv

1. How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum.
2. Assumption: It takes approximately 1000 m/s of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition.
3. Note: This equation is an guess, approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate."

• Equation for Kerbin Atmospheric Escape:

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}}$

• Simplified:

True Δv = ( ( Δv atm - 1000 ) / Δv atm ) * Δv vac + 1000

• Explained:

True Δv = ( ( Total Δv in atmosphere - 1000 m/s) / Total Δv in atmosphere ) X Total Δv in vacuum + 1000

• Example:

Single Stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum.

Transitional Δv = ( ( 5000 Δv atm - 1000 Δv Required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 1000 Δv Required to escape Kerbin atmosphere = Total Δv of 5800 m/s

See also

• Tutorials
• Terminology
• The Drawing Board: A library of tutorials and other useful information