Difference between revisions of "Cheat sheet/ja"

Revision as of 17:52, 17 March 2017 (view source) Rocketing Rudolph (talk | contribs) m (Blanked the page) ← Older edit		Revision as of 18:46, 17 March 2017 (view source) Sal vager (talk | contribs) m (Reverted edits by Rocketing Rudolph (talk) to last revision by TA) Newer edit →
Line 1:		Line 1:
		+	{{Outdated|
		+	* このページにある、大気のある惑星で必要なΔvは誤っています。その他の情報も更新するか削除する必要があります。
		+	* Δvマップは最新のものではありません。
		+	}}
		+
		+	KSP専門科学者用'''チートシート（カンペ）'''では、ゲームできっと役立つデルタVマップ、方程式などの情報を提供します。
		+
		+	== 数学 ==
		+	=== 推力重量比 (TWR) ===
		+	{{See also|Thrust-to-weight ratio}}
		+	運動の第2法則。この値が1以下だとロケットは上昇できない。離陸するには、その星の重力加速度より大きな加速度、つまり重力より大きな力が必要。
		+
		+	{{Formula|math=\text{TWR} = \frac{F_T}{m \cdot g} > 1|where=* <math>F_T</math> はエンジンの推力
		+	* <math>m</math> は機体の質量
		+	* <math>g</math> はその場の重力加速度（多くの場合、表面重力）}}
		+
		+	=== 合成比推力(I<sub>sp</sub>) ===
		+	{{See also|Specific impulse#Multiple engines|Specific impulse}}
		+	複数エンジンを使っていて、それぞれのエンジンのI<sub>sp</sub>がすべて同じなら、そのステージのI<sub>sp</sub>はその値に等しい。それぞれのエンジンでI<sub>sp</sub>が異なる場合、そのステージのI<sub>sp</sub>は次のようになる。
		+
		+	<math>I_{sp} = \frac{(F_1 + F_2 + \dots)}{\frac{F_1}{I_{sp1}} + \frac{F_2}{I_{sp2}} + \dots}</math>
		+
		+	=== デルタv (&Delta;v) ===
		+	==== 基本的な計算法 ====
		+	{{See also|Tutorial:Advanced Rocket Design}}
		+	大気がある場合とない場合で別々にデルタvを計算する。
		+	{{Formula|math=\Delta{v} = ln\left(\frac{M_{start} }{M_{end} }\right) \cdot I_{sp} \cdot 9.81 \frac{m}{s^2}|where=
		+	* <math>\Delta{v}</math> は変化可能な速度(m/s)
		+	* <math>M_{start}</math> は始めの質量
		+	* <math>M_{end}</math> は終わりの質量
		+	* <math>I_{sp}</math> は比推力(s)}}
		+
		+	==== 大気中と真空中をまたぐ場合の移行&Delta;v ====
		+	{| class="wikitable" style="float:left;margin:0.5em;"
		+	! Body !! &Delta;v<sub>out</sub>
		+	|-
		+	| [[Kerbin]] || 1000&nbsp;m/s
		+	|-
		+	| colspan="2" | other bodies' data missing
		+	|}
		+	&Delta;v<sub>out</sub>はその天体の大気圏を脱するのに必要な&Delta;v（周回軌道到達では''ない''）。この方程式で大気から真空へ移行するステージの実際の&Delta;vを計算することができる。
		+
		+	<math>\Delta{v}_T = \frac{\Delta{v}_{atm} - \Delta{v}_{out}}{\Delta{v}_{atm}} \cdot \Delta{v}_{vac} + \Delta{v}_{out}</math>
		+	{{clear|left}}
		+
		+	==== &Delta;vマップ ====
		+	各天体へ行くのに必要な&Delta;vをまとめた図。ファンによってこれまで色んなパターンのものが作られている。
		+
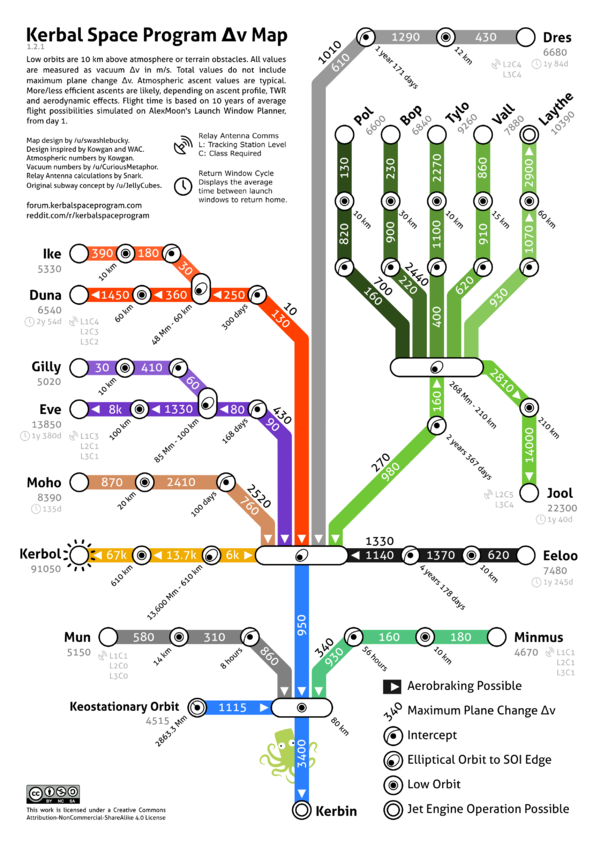
		+	'''路線図式&Delta;vマップ''(KSP 1.0.5)'':'''
		+	[[File:KerbinDeltaVMap.png|center|600px|&Delta;v to all bodies in the [[Kerbol System]]]]
		+
		+
		+	'''Total &Delta;v values'''
		+	* http://www.skyrender.net/lp/ksp/system_map.png
		+	'''&Delta;v change values'''
		+	* http://i.imgur.com/duY2S.png
		+	'''&Delta;v with Phase Angles'''
		+	* http://i.imgur.com/dXT6r7s.png
		+	'''Precise Total &Delta;v values'''
		+	* http://i.imgur.com/UUU8yCk.png
		+	'''WAC's &Delta;v Map for KSP 1.0.4'''
		+	* http://i.imgur.com/q0gC9H7.png
		+
		+	==== 最高&Delta;v表 ====
		+	:シングルステージの惑星間航行船にどのエンジンを積んだらよいか分かる早見表。どれだけ沢山の燃料を積んだとしても、ステージを切り離したり、スイングバイをしない限り、この&Delta;Vを超えることはできない。
		+	:{| class="wikitable"
		+	|-
		+	! ISP (s) !! 最高&Delta;v (m/s) !! エンジン名
		+	|-
		+	| 250 || 5394 || O-10 "Puff"
		+	|-
		+	| 290 || 6257 || LV-1R <br /> 24-77 "Twitch"
		+	|-
		+	| 300 || 6473 || KR-1x2 "Twin-Boar" <br /> LV-T30 "Reliant"<br /> 48-7S "Spark"
		+	|-
		+	| 305 || 6581 || CR-7 R.A.P.I.E.R. <br /> Mk-55 "Thud"
		+	|-
		+	| 310 || 6689 || Rockomax "Mainsail"
		+	|-
		+	| 315 || 6797|| LV-1 "Ant" <br /> KS-25x4 "Mammoth"
		+	|-
		+	| 320 || 6905 || LV-T45 <br /> Rockomax "Skipper"
		+	|-
		+	| 340 || 7336 || KR-2L <br /> Aerospike
		+	|-
		+	| 345 || 7444 || LV-909
		+	|-
		+	| 350 || 7552 || Poodle
		+	|-
		+	| 800 || 17261 || LV-N
		+	|}
		+	(Version: 1.04)
		+
		+	== 計算例 ==
		+	=== TWR ===
		+	*コピーテンプレート:
		+	::'''TWR = F / (m * g) > 1'''
		+
		+	=== I<sub>sp</sub> ===
		+	#各エンジンのI<sub>sp</sub>がすべて同じなら、そのI<sub>sp</sub>がステージのI<sub>sp</sub>である。だから、200I<sub>sp</sub>のエンジンを6基積んでも合計I<sub>sp</sub>は200。
		+	#各エンジンでI<sub>sp</sub>が異なるなら、次の方程式を使う、
		+
		+	*方程式:
		+	<math>I_{sp} = \frac{(F_1 + F_2 + \dots)}{\frac{F_1}{I_{sp1}} + \frac{F_2}{I_{sp2}} + \dots}</math>
		+
		+	*簡略化:
		+	::'''I<sub>sp</sub> = ( F1 + F2 + ... ) / ( ( F1 / I<sub>sp</sub>1 ) + ( F2 / I<sub>sp</sub>2 ) + ... )'''
		+
		+	*説明:
		+	::I<sub>sp</sub> = ( 第1エンジンの推力 + 第2エンジンの推力...続く... ) / ( ( 第1エンジンの推力 / 第1エンジンのI<sub>sp</sub> ) + ( 第2エンジンの推力 / 第2エンジンのI<sub>sp</sub> ) + ...続く... )
		+
		+	*例:
		+	:エンジンが2つあって、1つは推力が200ニュートン、I<sub>sp</sub>が120秒である。もう1つは推力が50ニュートン、I<sub>sp</sub>が200秒だったとする。
		+	:Isp = (200ニュートン+ 50ニュートン) / ( ( 200ニュートン / 120秒 ) + ( 50ニュートン / 200秒 ) = 130.4347826秒
		+
		+	=== &Delta;v ===
		+	#大気中の&Delta;vを計算するときは、大気中の比推力を使う。
		+	#真空中の&Delta;vを計算するときは、真空中の比推力を使う。
		+	#次の方程式を使って、あるステージの&Delta;vを計算する。
		+
		+	*方程式:
		+	<math>\Delta{v} = ln\left(\frac{M_{start}}{M_{dry}}\right) \cdot I_{sp} \cdot 9.81 \frac{m}{s^2}</math>
		+
		+	*簡略化:
		+	::'''&Delta;v = ln ( Mstart / Mdry ) * I<sub>sp</sub> * g'''
		+
		+	*説明:
		+	::&Delta;v = ln ( 初めの質量 / 終わりの質量 ) X Isp X 9.81
		+
		+	*例:
		+	:重さ23トンのシングルステージのロケットがある。燃焼終了すると15トンになる。エンジンの出力は120秒I<sub>sp</sub>
		+	:&Delta;v = ln ( 23トン / 15トン ) × 120秒 I<sub>sp</sub> × 9.81m/s² = 総&Delta;v 503.0152618 m/s
		+
		+	=== 最高&Delta;v ===
		+	:あるI<sub>sp</sub>の機体が発揮しうる最高&Delta;vを簡略版計算法。ここではエンジンの質量0、ペイロードなしとする。
		+	*方程式:
		+	::<math>\Delta{v} = 21.576745349086 \cdot I_{sp}</math>
		+	*簡略化:
		+	::'''&Delta;v =21.576745349086 * I<sub>sp</sub>'''
		+	*説明・例:
		+	:この計算では、燃料タンクの質量しか使わず、&Delta;v方程式のln ( Mstart / Mdry )部分のMstart / Mdryを、燃料消費量によらず9で一定とする（タンクによってはこれより悪い値）
		+	:以下の例では、シングルステージ、燃料タンクはT-100からJumbo 64の範囲、エンジン出力は380秒I<sub>sp</sub>とする。
		+	:最高&Delta;v = ln ( 18トン / 2トン ) × 380秒I<sub>sp</sub> × 9.81m/s²
		+	:最高&Delta;v = 2.1972245773 × 380秒I<sub>sp</sub> × 9.82m/s²(他に質量はないため、タンク数に関わりなく定数である全質量対乾質量の比で、質量のlogを置き換えた）
		+	:最高&Delta;v = 21.576745349086 × 380秒I<sub>sp</sub> = 8199.1632327878 m/s (定数をすべて約した）
		+
		+	=== 移行&Delta;v ===
		+	#Kerbinの大気から真空まで移動するロケットの&Delta;vの計算法。
		+	#前提: Kerbinの大気圏を脱出するにはおよそ1000&nbsp;m/sの&Delta;vがいる。
		+	#注意: この方程式は、推量、おおよそのものであって、100%正確ではない。この方程式を考案したフォーラムユーザーのstupid_chrisによれば、「結果はTWRとかによって少し違ってくるけど、基本的にくそ正しい。」
		+
		+	*Kerbin大気圏脱出の方程式:
		+	<math>\Delta{v}_T = \frac{\Delta{v}_{atm} - \Delta{v}_{out}}{\Delta{v}_{atm}} \cdot \Delta{v}_{vac} + \Delta{v}_{out}</math>
		+	{{clear|left}}
		+
		+	*簡略化:
		+	::'''True &Delta;v = ( ( &Delta;v atm - 1000 ) / &Delta;v atm ) * &Delta;v vac + 1000'''
		+
		+	*説明:
		+	::移行&Delta;v = ( ( 総大気中&Delta;v - 1000 m/s) / 総大気中&Delta;v) X 総真空中&Delta;v + 1000
		+
		+	*例:
		+	:シングルステージかつ、大気中の総&Delta;vが5000 m/s、真空中が6000とする。
		+	:移行&Delta;v = ( ( 5000大気&Delta;v - 1000大気脱出&Delta;v ) / 5000大気&Delta;v) X 6000真空&Delta;v + 1000大気脱出&Delta;v = 5800 m/s
		+
		+	== 参照 ==
		+
		+	* [[Tutorials/ja|チュートリアル]]
		+	* [[Terminology/ja|用語]]
		+	* [[thread:28352|The Drawing Board: A library of tutorials and other useful information]]

---

Revision as of 18:46, 17 March 2017

This page or section is in need of being brought up to date. Please help Kerbal Space Program Wiki by fixing inaccurate or outdated information. このページにある、大気のある惑星で必要なΔvは誤っています。その他の情報も更新するか削除する必要があります。 Δvマップは最新のものではありません。

KSP専門科学者用チートシート（カンペ）では、ゲームできっと役立つデルタVマップ、方程式などの情報を提供します。

数学

推力重量比 (TWR)

→ 参照： Thrust-to-weight ratio

運動の第2法則。この値が1以下だとロケットは上昇できない。離陸するには、その星の重力加速度より大きな加速度、つまり重力より大きな力が必要。

合成比推力(I_sp)

→ 参照： Specific impulse

複数エンジンを使っていて、それぞれのエンジンのI_spがすべて同じなら、そのステージのI_spはその値に等しい。それぞれのエンジンでI_spが異なる場合、そのステージのI_spは次のようになる。

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

デルタv (Δv)

基本的な計算法

→ 参照： Tutorial:Advanced Rocket Design

大気がある場合とない場合で別々にデルタvを計算する。

大気中と真空中をまたぐ場合の移行Δv

Body	Δvout
Kerbin	1000 m/s
other bodies' data missing

Δv_outはその天体の大気圏を脱するのに必要なΔv（周回軌道到達ではない）。この方程式で大気から真空へ移行するステージの実際のΔvを計算することができる。

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}}$

Δvマップ

各天体へ行くのに必要なΔvをまとめた図。ファンによってこれまで色んなパターンのものが作られている。

路線図式Δvマップ(KSP 1.0.5):

Total Δv values

• http://www.skyrender.net/lp/ksp/system_map.png

Δv change values

• http://i.imgur.com/duY2S.png

Δv with Phase Angles

• http://i.imgur.com/dXT6r7s.png

Precise Total Δv values

• http://i.imgur.com/UUU8yCk.png

WAC's Δv Map for KSP 1.0.4

• http://i.imgur.com/q0gC9H7.png

最高Δv表

シングルステージの惑星間航行船にどのエンジンを積んだらよいか分かる早見表。どれだけ沢山の燃料を積んだとしても、ステージを切り離したり、スイングバイをしない限り、このΔVを超えることはできない。

ISP (s)	最高Δv (m/s)	エンジン名
250	5394	O-10 "Puff"
290	6257	LV-1R 24-77 "Twitch"
300	6473	KR-1x2 "Twin-Boar" LV-T30 "Reliant" 48-7S "Spark"
305	6581	CR-7 R.A.P.I.E.R. Mk-55 "Thud"
310	6689	Rockomax "Mainsail"
315	6797	LV-1 "Ant" KS-25x4 "Mammoth"
320	6905	LV-T45 Rockomax "Skipper"
340	7336	KR-2L Aerospike
345	7444	LV-909
350	7552	Poodle
800	17261	LV-N

(Version: 1.04)

計算例

TWR

• コピーテンプレート:

TWR = F / (m * g) > 1

I_sp

1. 各エンジンのI_spがすべて同じなら、そのI_spがステージのI_spである。だから、200I_spのエンジンを6基積んでも合計I_spは200。
2. 各エンジンでI_spが異なるなら、次の方程式を使う、

• 方程式:

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

• 簡略化:

I_sp = ( F1 + F2 + ... ) / ( ( F1 / I_sp1 ) + ( F2 / I_sp2 ) + ... )

• 説明:

I_sp = ( 第1エンジンの推力 + 第2エンジンの推力...続く... ) / ( ( 第1エンジンの推力 / 第1エンジンのI_sp ) + ( 第2エンジンの推力 / 第2エンジンのI_sp ) + ...続く... )

• 例:

エンジンが2つあって、1つは推力が200ニュートン、I_spが120秒である。もう1つは推力が50ニュートン、I_spが200秒だったとする。

Isp = (200ニュートン+ 50ニュートン) / ( ( 200ニュートン / 120秒 ) + ( 50ニュートン / 200秒 ) = 130.4347826秒

Δv

1. 大気中のΔvを計算するときは、大気中の比推力を使う。
2. 真空中のΔvを計算するときは、真空中の比推力を使う。
3. 次の方程式を使って、あるステージのΔvを計算する。

• 方程式:

${\displaystyle \Delta {v}=ln\left({\frac {M_{start}}{M_{dry}}}\right)\cdot I_{sp}\cdot 9.81{\frac {m}{s^{2}}}}$

• 簡略化:

Δv = ln ( Mstart / Mdry ) * I_sp * g

• 説明:

Δv = ln ( 初めの質量 / 終わりの質量 ) X Isp X 9.81

• 例:

重さ23トンのシングルステージのロケットがある。燃焼終了すると15トンになる。エンジンの出力は120秒I_sp

Δv = ln ( 23トン / 15トン ) × 120秒 I_sp × 9.81m/s² = 総Δv 503.0152618 m/s

最高Δv

あるI_spの機体が発揮しうる最高Δvを簡略版計算法。ここではエンジンの質量0、ペイロードなしとする。

• 方程式:

${\displaystyle \Delta {v}=21.576745349086\cdot I_{sp}}$

• 簡略化:

Δv =21.576745349086 * I_sp

• 説明・例:

この計算では、燃料タンクの質量しか使わず、Δv方程式のln ( Mstart / Mdry )部分のMstart / Mdryを、燃料消費量によらず9で一定とする（タンクによってはこれより悪い値）

以下の例では、シングルステージ、燃料タンクはT-100からJumbo 64の範囲、エンジン出力は380秒I_spとする。

最高Δv = ln ( 18トン / 2トン ) × 380秒I_sp × 9.81m/s²

最高Δv = 2.1972245773 × 380秒I_sp × 9.82m/s²(他に質量はないため、タンク数に関わりなく定数である全質量対乾質量の比で、質量のlogを置き換えた）

最高Δv = 21.576745349086 × 380秒I_sp = 8199.1632327878 m/s (定数をすべて約した）

移行Δv

1. Kerbinの大気から真空まで移動するロケットのΔvの計算法。
2. 前提: Kerbinの大気圏を脱出するにはおよそ1000 m/sのΔvがいる。
3. 注意: この方程式は、推量、おおよそのものであって、100%正確ではない。この方程式を考案したフォーラムユーザーのstupid_chrisによれば、「結果はTWRとかによって少し違ってくるけど、基本的にくそ正しい。」

• Kerbin大気圏脱出の方程式:

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}}$

• 簡略化:

True Δv = ( ( Δv atm - 1000 ) / Δv atm ) * Δv vac + 1000

• 説明:

移行Δv = ( ( 総大気中Δv - 1000 m/s) / 総大気中Δv) X 総真空中Δv + 1000

• 例:

シングルステージかつ、大気中の総Δvが5000 m/s、真空中が6000とする。

移行Δv = ( ( 5000大気Δv - 1000大気脱出Δv ) / 5000大気Δv) X 6000真空Δv + 1000大気脱出Δv = 5800 m/s

参照

• チュートリアル
• 用語
• The Drawing Board: A library of tutorials and other useful information