Difference between revisions of "Cheat sheet"
m (→True Δv of a stage that crosses from atmosphere to vacuum) |
m (→True Δv of a stage that crosses from atmosphere to vacuum) |
||
| Line 29: | Line 29: | ||
! Body !! Δv<sub>out</sub> | ! Body !! Δv<sub>out</sub> | ||
|- | |- | ||
| − | | [[Kerbin]] || 1000 m/s | + | | [[Kerbin]] || 1000 m/s |
|- | |- | ||
| colspan="2" | other bodies' data missing | | colspan="2" | other bodies' data missing | ||
Revision as of 08:06, 21 February 2014
Kerbal Space Program rocket scientist's cheat sheet: Delta-v maps, equations and more for your reference so you can get from here to there and back again.
Contents
Mathematics
Thrust to Weight Ratio (TWR)
- → See also: Thrust-to-weight ratio
This is Newton's Second Law. If the ratio is less than 1 the craft will not lift off the ground. Note that the local gravitational acceleration, which is usually the surface gravity of the body the rocket is starting from, is required.
- is the thrust of the engines
- the total mass of the craft
- the local gravitational acceleration (usually surface gravity)
Combined Specific Impulse (Isp)
- → See also: Specific impulse
If the Isp is the same for all engines in a stage, then the Isp is equal to a single engine. If the Isp is different for engines in a single stage, then use the following equation:
Delta-v (Δv)
Basic calculation
- → See also: Tutorial:Advanced Rocket Design
Basic calculation of a rocket's Δv. Use the atmospheric and vacuum thrust values for atmospheric and vacuum Δv, respectively.
- is the velocity change possible in m/s
- is the starting mass in the same unit as
- is the end mass in the same unit as
- is the specific impulse of the engine in seconds
True Δv of a stage that crosses from atmosphere to vacuum
| Body | Δvout |
|---|---|
| Kerbin | 1000 m/s |
| other bodies' data missing | |
Calculation of a rocket stage's Δv, taking into account transitioning from atmosphere to vacuum. Δvout is the amount of Δv required to leave a body's atmosphere, not reach orbit. This equation is useful to figure out the actual Δv of a stage that transitions from atmosphere to vacuum.
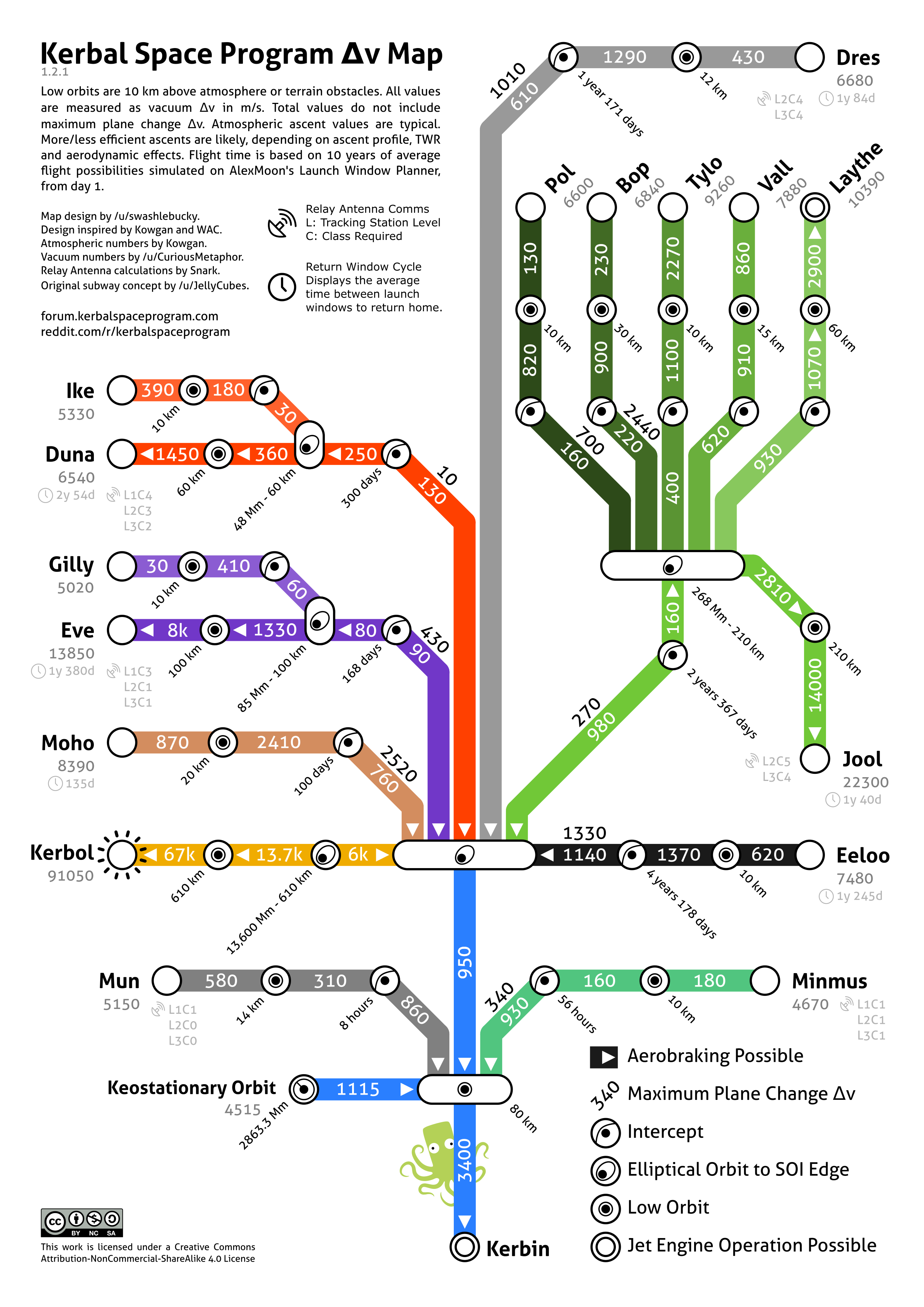
Maps
Various fan-made maps showing the Δv required to travel to a certain body.
Subway style Δv map:
Total Δv values
Δv change values
Δv nomogram
Δv with Phase Angles
Precise Total Δv values
Math examples
TWR
- Copy template:
- TWR = F / (m * g) > 1
Isp
- When Isp is the same for all engines in a stage, then the Isp is equal to a single engine. So six 200 Isp engines still yields only 200 Isp.
- When Isp is different for engines in a single stage, then use the following equation:
- Equation:
- Simplified:
- Isp = ( F1 + F2 + ... ) / ( ( F1 / Isp1 ) + ( F2 / Isp2 ) + ... )
- Explained:
- Isp = ( Force of Thrust of 1st Engine + Force of Thrust of 2nd Engine...and so on... ) / ( ( Force of Thrust of 1st Engine / Isp of 1st Engine ) + ( Force of Thrust of 2nd Engine / Isp of 2nd Engine ) + ...and so on... )
- Example:
- Two engines, one rated 200 newtons and 120 seconds Isp ; another engine rated 50 newtons and 200 seconds Isp.
- Isp = (200 newtons + 50 newtons) / ( ( 200 newtons / 120 ) + ( 50 newtons / 200 ) = 130.89 seconds Isp
Δv
- For atmospheric Δv value, use atmospheric thrust values.
- For vacuum Δv value, use vacuum thrust values.
- Use this equation to figure out the Δv per stage:
- Equation:
- Simplified:
- Δv = ln ( Mstart / Mdry ) * Isp * g
- Explained:
- Δv = ln ( Starting Mass / Dry Mass ) X Isp X 9.81
- Example:
- Single Stage Rocket that weighs 23 tons when full, 15 tons when fuel is emptied, and engine that outputs 120 seconds Isp.
- Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds Isp × 9.81m/s² = Total Δv of 503.2 m/s
True Δv
- How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum.
- Assumption: It takes approximately 1000 m/s2 of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition.
- Note: This equation is an guess, approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate."
- Equation for Kerbin Atmospheric Escape:
- Simplified:
- True Δv = ( ( Δv atm - 1000 ) / Δv atm ) * Δv vac + 1000
- Explained:
- True Δv = ( ( Total Δv in atmosphere - 1000 m/s2) / Total Δv in atmosphere ) X Total Δv in vacuum + 1000
- Example:
- Single Stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum.
- Transitional Δv = ( ( 5000 Δv atm - 1000 Δv Required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 1000 Δv Required to escape Kerbin atmosphere = Total Δv of 5800 m/s