Difference between revisions of "Cheat sheet/fr"
(→Combined Specific Impulse (Isp)) |
(Added category.) |
||
| (27 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | La Bible de l'astronome ''Kerbal Space Program'' : cartes de delta-v, équations et toutes les informations et références qui vous permettront d'aller | + | La Bible de l'astronome ''Kerbal Space Program'' : cartes de delta-v, équations et toutes les informations et références qui vous permettront d'aller où bon vous semble dans le système [[Kerbol|kerbollien]], et de revenir. |
| − | Ceci est une traduction de [[Cheat sheet|la version anglaise]] | + | Ceci est une traduction de [[Cheat sheet|la version anglaise]] par ''Mixoupe''. |
== Formules et théorie == | == Formules et théorie == | ||
=== Ratio poussée-poids (TWR) === | === Ratio poussée-poids (TWR) === | ||
| − | {{See also| | + | {{See also|Tutorial:Intermediate Rocket Design/fr#Ratio poussée-poids (thrust-weight ratio)|Ratio poussée-poids}} |
| − | Si le ratio poussée-poids (thrust-yo-weight ration, TWR) est | + | Si le ratio poussée-poids (thrust-yo-weight ration, TWR) est inférieur à 1, la fusée ne décollera pas du pas de tir. On utilise ici l'accélération de la pesanteur au niveau du sol (<math>g_0=9,81m/s^2</math> pour [[Kerbin]])<ref>[http://fr.wikipedia.org/wiki/Lois_du_mouvement_de_Newton#Deuxi.C3.A8me_loi_de_Newton_ou_principe_fondamental_de_la_dynamique_de_translation la seconde loi de Newton]</ref>. |
:<math>TWR = \frac{F}{m \cdot g_0}>1</math> | :<math>TWR = \frac{F}{m \cdot g_0}>1</math> | ||
| Line 13: | Line 13: | ||
Où | Où | ||
| − | * <math>F</math> est la force de poussée des moteurs (en newtons. | + | * <math>F</math> est la force de poussée des moteurs (en newtons). |
* <math>m</math> est la masse totale du vaisseau (en kilogrammes). | * <math>m</math> est la masse totale du vaisseau (en kilogrammes). | ||
=== Impulsion spécifique combinée === | === Impulsion spécifique combinée === | ||
| − | {{See also|Tutorial: Advanced Rocket Design/fr#Moteurs multiples}} | + | {{See also|Tutorial:Advanced Rocket Design/fr#Moteurs multiples|Impulsion spécifique combinée}} |
| − | + | Si l'impulsion spécifique (<math>I_{sp}</math>) est la même pour tous les moteurs, alors est la même que pour un seul moteur. Si <math>I_{sp}</math> est différent pour différents moteurs d'un même étage, on évalue l'impulsion moyenne par la formule suivante : | |
| − | <math>I_{sp} = \frac{(F_1 + F_2 + \dots)}{\frac{F_1}{I_{sp1}} + \frac{F_2}{I_{sp2}} + \dots}</math> | + | :<math>I_{sp} = \frac{(F_1 + F_2 + \dots)}{\frac{F_1}{I_{sp1}} + \frac{F_2}{I_{sp2}} + \dots}</math> |
=== Delta-v (Δv) === | === Delta-v (Δv) === | ||
| − | ==== | + | ==== Calculs de base ==== |
| − | {{See also|Tutorial:Advanced Rocket Design}} | + | {{See also|Tutorial:Advanced Rocket Design/fr}} |
| − | + | ||
| − | + | En fonction que vous soyez dans l'atmosphère ou dans le vide, utilisez la valeur de poussée dans l'atmosphère ou dans le vide, respectivement. | |
| − | * <math> | + | |
| − | * <math> | + | |
| − | + | :<math>\Delta v= g_{0} \cdot I_{sp} \cdot ln \frac{m_\text{initiale}}{m_\text{finale}}</math> | |
| + | |||
| + | Où | ||
| + | |||
| + | * <math>\Delta v</math> est la variation de vitesse (en mètres par seconde). | ||
| + | * <math>g_0=9,81m/s^2</math>. | ||
| + | * <math>I_{sp}</math> est l'impulsion spécifique (en secondes). | ||
| + | * <math>m_\text{initiale}</math> et <math>m_\text{finale}</math> sont les masses avant et après la poussée (dans la même unité). | ||
| + | |||
| + | ==== Δv vrai d'un étage traversant l'atmosphère ==== | ||
| + | |||
| − | |||
{| class="wikitable" style="float:left;margin:0.5em;" | {| class="wikitable" style="float:left;margin:0.5em;" | ||
| − | ! | + | ! Corps !! Δv<sub>out</sub> |
|- | |- | ||
| − | | [[Kerbin]] || 1000 | + | | [[Kerbin]] || 1000 m/s |
|- | |- | ||
| − | | | + | | Autre corps || Données manquantes |
|} | |} | ||
| − | |||
| − | <math>\Delta{v}_T = \frac{\Delta{v}_{atm} - \Delta{v}_{out}}{\Delta{v}_{atm}} \cdot \Delta{v}_{vac} + \Delta{v}_{out}</math> | + | Calcul du <math>\Delta v</math> additionnel nécessaire pour quitter l'atmosphère. C'est la valeur de <math>\Delta v</math> requise pour quitter l'atmosphère, '''pas''' pour atteindre l'orbite. Ce <math>\Delta v</math> est à ajouter au <math>\Delta v</math> pour la mise en orbite dans le dimensionnement du premier étage d'une fusée. |
| + | |||
| + | :<math>\Delta{v}_T = \frac{\Delta{v}_{atm} - \Delta{v}_{out}}{\Delta{v}_{atm}} \cdot \Delta{v}_{vac} + \Delta{v}_{out}</math> | ||
{{clear|left}} | {{clear|left}} | ||
| − | ==== | + | ==== Cartes de Δv ==== |
| − | |||
| − | ''' | + | {{See also|Tutorial:Advanced Rocket Design/fr#Bilan de delta-v}} |
| + | |||
| + | Différentes carte de <math>\Delta v</math> faites par les utilisateurs pour desser votre bilan de <math>\Delta v</math> entre deux endroits. | ||
| + | |||
| + | '''Cartes de Δv de style ''carte de métro''''' | ||
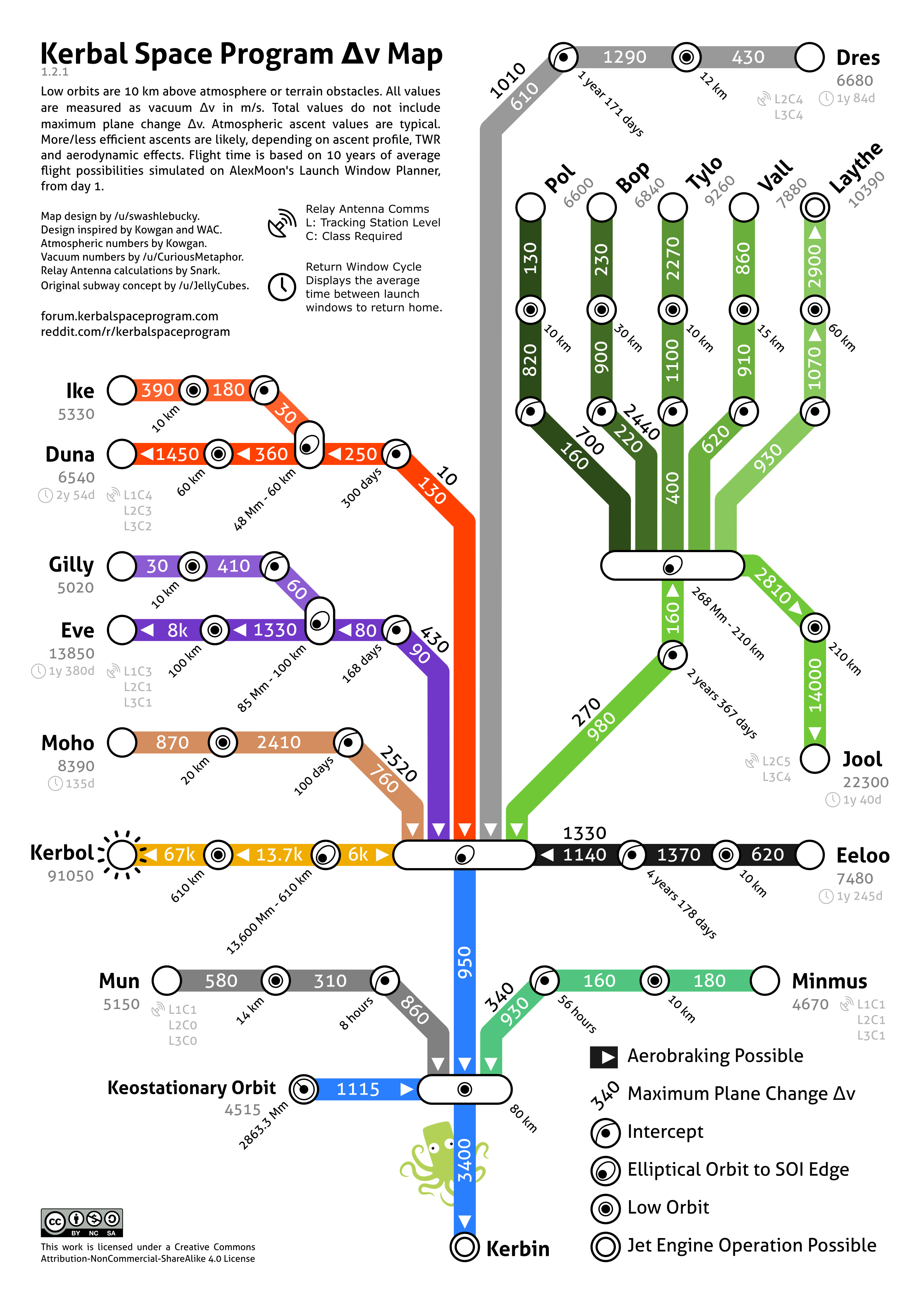
[[File:KerbinDeltaVMap.png|center|Δv to all bodies in the [[Kerbol System]]]] | [[File:KerbinDeltaVMap.png|center|Δv to all bodies in the [[Kerbol System]]]] | ||
| Line 63: | Line 76: | ||
* http://i.imgur.com/UUU8yCk.png | * http://i.imgur.com/UUU8yCk.png | ||
| − | == | + | == Exemples == |
| − | === | + | === Ratio poussée-poids === |
| − | * | + | *Equation : |
::'''TWR = F / (m * g) > 1''' | ::'''TWR = F / (m * g) > 1''' | ||
=== I<sub>sp</sub> === | === I<sub>sp</sub> === | ||
| − | # | + | #Quand I<sub>sp</sub> est le même pour tous les moteurs d'un étage, alors I<sub>sp</sub> est le même que pour un seul moteur. donc six moteurs avec <math>I_{sp}=200s</math> donne un I<sub>sp</sub> de 200 s. |
| − | # | + | #Quand I<sub>sp</sub> varie pour les moteurs d'un même étage, on utilise l'équation suivante: |
| − | *Equation: | + | *Equation : |
<math>I_{sp} = \frac{(F_1 + F_2 + \dots)}{\frac{F_1}{I_{sp1}} + \frac{F_2}{I_{sp2}} + \dots}</math> | <math>I_{sp} = \frac{(F_1 + F_2 + \dots)}{\frac{F_1}{I_{sp1}} + \frac{F_2}{I_{sp2}} + \dots}</math> | ||
| − | * | + | *Simplifiée : |
::'''I<sub>sp</sub> = ( F1 + F2 + ... ) / ( ( F1 / I<sub>sp</sub>1 ) + ( F2 / I<sub>sp</sub>2 ) + ... )''' | ::'''I<sub>sp</sub> = ( F1 + F2 + ... ) / ( ( F1 / I<sub>sp</sub>1 ) + ( F2 / I<sub>sp</sub>2 ) + ... )''' | ||
| − | * | + | *Expliquée : |
| − | ::I<sub>sp</sub> = ( | + | ::I<sub>sp</sub> = ( poussée du 1er moteur + poussée du 2e moteur...etc... ) / ( ( poussée du 1er moteur / I<sub>sp</sub> du 1er moteur ) + ( poussée du 2e moteur / I<sub>sp</sub> du 2e moteur ) + ...etc... ) |
| + | |||
| + | *Exemple : | ||
| + | :Deux moteurs, le 1er F = 200 N et I<sub>sp</sub> = 120 s ; le 2e F = 50 N et I<sub>sp</sub> = 200 s. | ||
| + | :I<sub>sp</sub> = (200 N + 50 N) / ((200 N / 120) + (50 N / 200)) = 130,89 s. | ||
| − | |||
| − | |||
| − | |||
=== Δv === | === Δv === | ||
| − | |||
| − | |||
| − | |||
| − | + | #Pour des valeurs de <math>\Delta v</math> atmosphérique, utiliser des valeurs de poussée atmosphérique. | |
| − | <math>\Delta | + | #Pour des valeurs de <math>\Delta v</math> dans le vide, utiliser des valeurs de poussée dans le vide. |
| + | #Utiliser cette équation pour calculer le <math>\Delta v</math> par étage : | ||
| − | |||
| − | |||
| − | * | + | *Equation : |
| − | : | + | :<math>\Delta v = ln \left(\frac{m_\text{totale}}{m_\text{sèche}}\right) \cdot I_{sp} \cdot 9,81 \frac{m}{s^2}</math> |
| − | * | + | *Simplifiée : |
| − | : | + | ::'''Δv = ln ( Mtotale / Msèche ) * I<sub>sp</sub> * g''' |
| − | :Δv = ln ( | ||
| − | + | *Expliquée : | |
| − | + | ::Δv = ln ( masse initial / masse finale ) X Isp X 9.81 | |
| − | |||
| − | |||
| − | *Equation | + | *Exemple : |
| − | <math>\Delta{v} | + | :Fusée d'un étage de 23 tonnes (avec carburant), 15 tonnes sans carburant et avec moteurs I<sub>sp</sub> = 120 s. |
| + | :Δv = ln ( 23 t / 15 t ) × 120 s × 9.81m/s² = Δv total de 503.2 m/s. | ||
| + | |||
| + | === Δv vrai === | ||
| + | |||
| + | #comment calculer le <math>\Delta v</math> d'un étage qui passe de l'atmosphère de [[Kerbin]] au vide. | ||
| + | #Postulat : il faut approximativement 1000 m/s de <math>\Delta v</math> pour quitter l'atmosphère avant d'tiliser les valeurs de <math>\Delta v</math> dans le vide. | ||
| + | #Note : cette valeur est une estimation, approximée, et non fiable à 100 %. Donnée de l'utilisateur du forum ''stupid_chris'' : "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate". | ||
| + | |||
| + | |||
| + | *Equation pour quitter l'atmosphère de [[Kerbin]] : | ||
| + | |||
| + | <math>\Delta{v}_v = \frac{\Delta{v}_{atm} - \Delta{v}_{out}}{\Delta{v}_{atm}} \cdot \Delta{v}_{vac} + \Delta{v}_{out}</math> | ||
{{clear|left}} | {{clear|left}} | ||
| − | * | + | *Simplifiée : |
| − | ::''' | + | ::'''Δv vrai = ( ( Δv atm - 1000 ) / Δv atm ) * Δv vide + 1000''' |
| − | |||
| − | |||
| − | |||
| − | * | + | *Expliquée : |
| − | : | + | ::Δv vrai = ( ( Δv total dans l'atmosphère - 1000 m/s) / Δv total dans l'atmosphère ) X Δv total dans le vide + 1000 m/s |
| − | : | ||
| − | == | + | *Exemple : |
| + | :Fusée d'un étage avec Δv atmosphérique totale = 5 000 m/s, et un Δv dans le vide de 6 000 m/s | ||
| + | :Δv de transition = ( ( 5000 Δv atm - 1000 Δv requis pour quitter l'atmosphère ) / 5000 Δv atm ) X 6000 Δv vide + 1000 Δv requis pour quitter l'atmosphère = Δv total de 5800 m/s | ||
| − | + | [[Category: Articles/fr]] | |
| − | |||
| − | |||
Latest revision as of 11:08, 15 May 2021
La Bible de l'astronome Kerbal Space Program : cartes de delta-v, équations et toutes les informations et références qui vous permettront d'aller où bon vous semble dans le système kerbollien, et de revenir.
Ceci est une traduction de la version anglaise par Mixoupe.
Contents
Formules et théorie
Ratio poussée-poids (TWR)
- → See also: Ratio poussée-poids
Si le ratio poussée-poids (thrust-yo-weight ration, TWR) est inférieur à 1, la fusée ne décollera pas du pas de tir. On utilise ici l'accélération de la pesanteur au niveau du sol ( pour Kerbin)[1].
Où
- est la force de poussée des moteurs (en newtons).
- est la masse totale du vaisseau (en kilogrammes).
Impulsion spécifique combinée
- → See also: Impulsion spécifique combinée
Si l'impulsion spécifique () est la même pour tous les moteurs, alors est la même que pour un seul moteur. Si est différent pour différents moteurs d'un même étage, on évalue l'impulsion moyenne par la formule suivante :
Delta-v (Δv)
Calculs de base
- → See also: Tutorial:Advanced Rocket Design/fr
En fonction que vous soyez dans l'atmosphère ou dans le vide, utilisez la valeur de poussée dans l'atmosphère ou dans le vide, respectivement.
Où
- est la variation de vitesse (en mètres par seconde).
- .
- est l'impulsion spécifique (en secondes).
- et sont les masses avant et après la poussée (dans la même unité).
Δv vrai d'un étage traversant l'atmosphère
| Corps | Δvout |
|---|---|
| Kerbin | 1000 m/s |
| Autre corps | Données manquantes |
Calcul du additionnel nécessaire pour quitter l'atmosphère. C'est la valeur de requise pour quitter l'atmosphère, pas pour atteindre l'orbite. Ce est à ajouter au pour la mise en orbite dans le dimensionnement du premier étage d'une fusée.
Cartes de Δv
Différentes carte de faites par les utilisateurs pour desser votre bilan de entre deux endroits.
Cartes de Δv de style carte de métro
Total Δv values
Δv change values
Δv nomogram
Δv with Phase Angles
Precise Total Δv values
Exemples
Ratio poussée-poids
- Equation :
- TWR = F / (m * g) > 1
Isp
- Quand Isp est le même pour tous les moteurs d'un étage, alors Isp est le même que pour un seul moteur. donc six moteurs avec donne un Isp de 200 s.
- Quand Isp varie pour les moteurs d'un même étage, on utilise l'équation suivante:
- Equation :
- Simplifiée :
- Isp = ( F1 + F2 + ... ) / ( ( F1 / Isp1 ) + ( F2 / Isp2 ) + ... )
- Expliquée :
- Isp = ( poussée du 1er moteur + poussée du 2e moteur...etc... ) / ( ( poussée du 1er moteur / Isp du 1er moteur ) + ( poussée du 2e moteur / Isp du 2e moteur ) + ...etc... )
- Exemple :
- Deux moteurs, le 1er F = 200 N et Isp = 120 s ; le 2e F = 50 N et Isp = 200 s.
- Isp = (200 N + 50 N) / ((200 N / 120) + (50 N / 200)) = 130,89 s.
Δv
- Pour des valeurs de atmosphérique, utiliser des valeurs de poussée atmosphérique.
- Pour des valeurs de dans le vide, utiliser des valeurs de poussée dans le vide.
- Utiliser cette équation pour calculer le par étage :
- Equation :
- Simplifiée :
- Δv = ln ( Mtotale / Msèche ) * Isp * g
- Expliquée :
- Δv = ln ( masse initial / masse finale ) X Isp X 9.81
- Exemple :
- Fusée d'un étage de 23 tonnes (avec carburant), 15 tonnes sans carburant et avec moteurs Isp = 120 s.
- Δv = ln ( 23 t / 15 t ) × 120 s × 9.81m/s² = Δv total de 503.2 m/s.
Δv vrai
- comment calculer le d'un étage qui passe de l'atmosphère de Kerbin au vide.
- Postulat : il faut approximativement 1000 m/s de pour quitter l'atmosphère avant d'tiliser les valeurs de dans le vide.
- Note : cette valeur est une estimation, approximée, et non fiable à 100 %. Donnée de l'utilisateur du forum stupid_chris : "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate".
- Equation pour quitter l'atmosphère de Kerbin :
- Simplifiée :
- Δv vrai = ( ( Δv atm - 1000 ) / Δv atm ) * Δv vide + 1000
- Expliquée :
- Δv vrai = ( ( Δv total dans l'atmosphère - 1000 m/s) / Δv total dans l'atmosphère ) X Δv total dans le vide + 1000 m/s
- Exemple :
- Fusée d'un étage avec Δv atmosphérique totale = 5 000 m/s, et un Δv dans le vide de 6 000 m/s
- Δv de transition = ( ( 5000 Δv atm - 1000 Δv requis pour quitter l'atmosphère ) / 5000 Δv atm ) X 6000 Δv vide + 1000 Δv requis pour quitter l'atmosphère = Δv total de 5800 m/s