Difference between revisions of "Cheat sheet/fr"

Revision as of 19:32, 23 April 2014

La Bible de l'astronome Kerbal Space Program : cartes de delta-v, équations et toutes les informations et références qui vous permettront d'aller au bon vous semble dans le système kerbollien, et de revenir.

Ceci est une traduction de la version anglaise, en cours par Mixoupe.

Formules et théorie

Ratio poussée-poids (TWR)

→ See also: Ratio poussée-poids

Si le ratio poussée-poids (thrust-yo-weight ration, TWR) est unférieur à 1, la fusée ne décollera pas du pas de tir. On utilise ici l'accélération de la pesanteur au niveau du sol (${\displaystyle g_{0}=9,81m/s^{2}}$ pour Kerbin) et la seconde loi de Newton.

${\displaystyle TWR={\frac {F}{m\cdot g_{0}}}>1}$

Où

• ${\displaystyle F}$ est la force de poussée des moteurs (en newtons.
• ${\displaystyle m}$ est la masse totale du vaisseau (en kilogrammes).

Impulsion spécifique combinée

→ See also: Impulsion spécifique combinée

Si l'impulsion spécifique (${\displaystyle I_{sp}}$) est la même pour tous les moteurs, alors est la même que pour un seul moteur. Si ${\displaystyle I_{sp}}$ est différent pour différents moteurs d'un même étage, on évalue l'impulsion moyenne par la formule suivante :

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

Delta-v (Δv)

Calculs de base

→ See also: Tutorial:Advanced Rocket Design/fr

En fonction que vous soyez dans l'atmosphère ou dans le vide, utilisez la valeur de poussée dans l'atmosphère ou dans le vide, respectivement.

${\displaystyle \Delta v=g\cdot I_{sp}\cdot ln{\frac {m_{\text{initiale}}}{m_{\text{initiale}}}}}$

Où

• ${\displaystyle \Delta v}$ est la variation de vitesse (en mètres par seconde).
• ${\displaystyle g=g_{0}\cdot \left({\frac {R}{R+h}}\right)^{2}}$.
• ${\displaystyle g_{0}=9,81m/s^{2}}$.
• ${\displaystyle R}$ est le rayon du corps orbité (en mètres).
• ${\displaystyle h}$ est l'altitude (en mètres)
• ${\displaystyle I_{sp}}$ est l'impulsion spécifique (en secondes).
• ${\displaystyle m_{\text{initiale}}}$ et ${\displaystyle m_{\text{finale}}}$ sont les masses avant et après la poussée (dans la même unité).

Δv vrai d'un étage traversant l'atmosphère

Calcul du ${\displaystyle \Delta v}$ additionnel nécessaire pour quitter l'atmosphère. C'est la valeur de ${\displaystyle \Delta v}$ requise pour quitter l'atmosphère, pas pour atteindre l'orbite. Ce ${\displaystyle \Delta v}$ est à ajouter au ${\displaystyle \Delta v}$ pour la mise en orbite dans le dimensionnement du premier étage d'une fusée.

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}}$

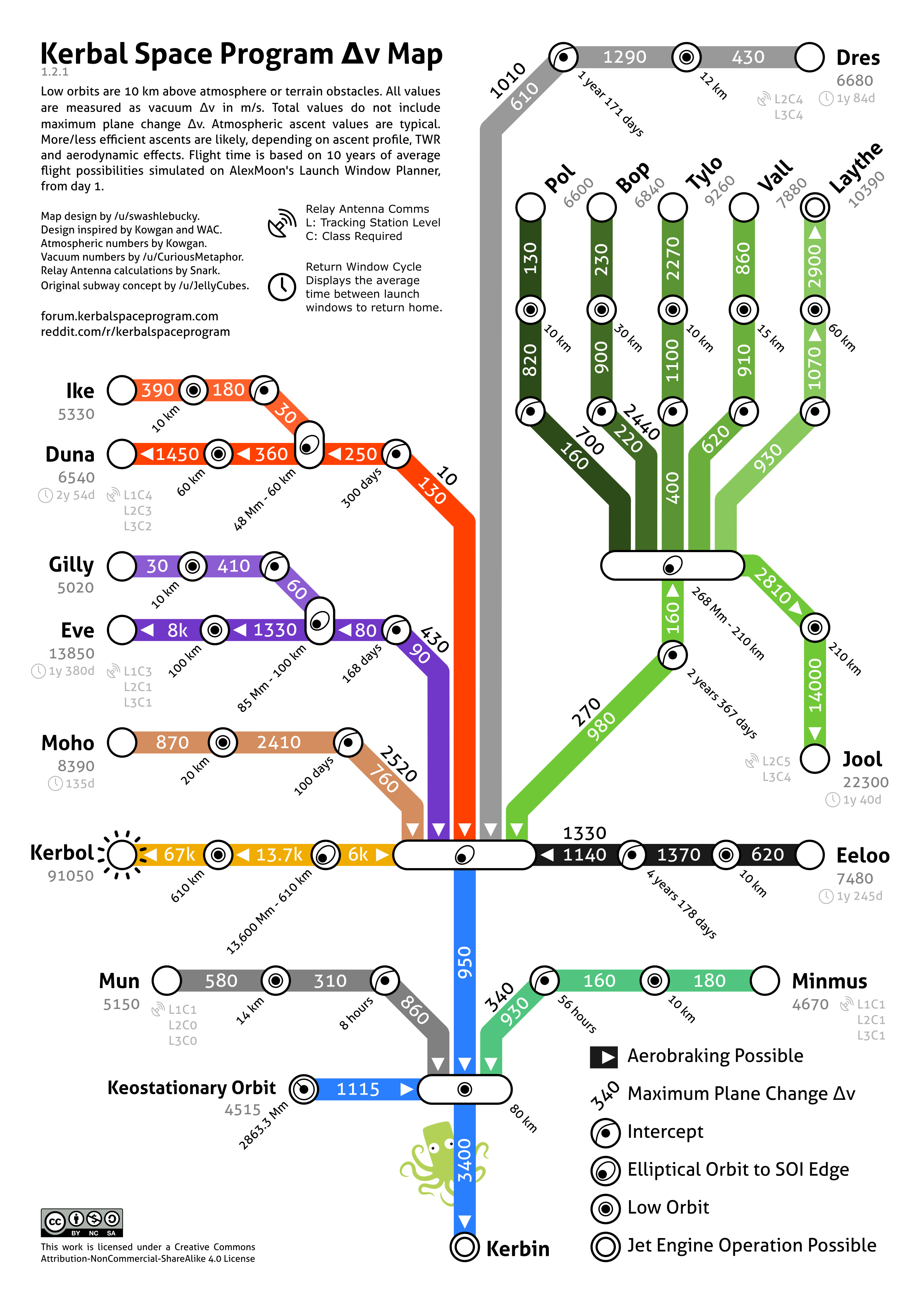
Cartes de Δv

→ See also: Tutorial:Advanced Rocket Design/fr#Bilan de delta-v

Différentes carte de ${\displaystyle \Delta v}$ faites par les utilisateurs pour desser votre bilan de ${\displaystyle \Delta v}$ entre deux endroits.

Cartes de Δv de style carte de métro

Total Δv values

• http://www.skyrender.net/lp/ksp/system_map.png

Δv change values

• http://i.imgur.com/duY2S.png

Δv nomogram

• http://ubuntuone.com/1kD39BCoV38WP1QeG6MtO6

Δv with Phase Angles

• http://i.imgur.com/dXT6r7s.png

Precise Total Δv values

• http://i.imgur.com/UUU8yCk.png

Exemples

Ration poussée-poids

• Copy template:

TWR = F / (m * g) > 1

I_sp

1. Quand I_sp est le même pour tous les moteurs d'un étage, alors I_sp est le même que pour un seul moteur. donc six moteurs avec ${\displaystyle I_{sp}=200s}$ donne un I_sp de 200 s.
2. Quand I_sp varie pour les moteurs d'un même étage, on utilise l'équation suivante:

• Equation :

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

• Simplifiée :

I_sp = ( F1 + F2 + ... ) / ( ( F1 / I_sp1 ) + ( F2 / I_sp2 ) + ... )

• Expliquée :

I_sp = ( poussée du 1er moteur + poussée du 2e moteur...etc... ) / ( ( poussée du 1er moteur / I_sp du 1er moteur ) + ( poussée du 2e moteur / I_sp du 2e moteur ) + ...etc... )

• Exemple :

Deux moteurs, le 1er F = 200 N et I_sp = 120 s ; le 2e F = 50 N et I_sp = 200 s.

I_sp = (200 N + 50 N) / ((200 N / 120) + (50 N / 200)) = 130,89 s.

Δv

1. Pour des valeurs de ${\displaystyle \Delta v}$ atmosphérique, utiliser des valeurs de poussée atmosphérique.
2. Pour des valeurs de ${\displaystyle \Delta v}$ dans le vide, utiliser des valeurs de poussée dans le vide.

Utiliser cette équation pour calculer le ${\displaystyle \Delta v}$ par étage :

• Equation :

Failed to parse (syntax error): {\displaystyle \Delta{v} = ln\left(\frac{M_{totale}}{M_{sèche}}\right) \cdot I_{sp} \cdot 9,81 \frac{m}{s^2}}

• Simplified:

Δv = ln ( Mtotale / Msèche ) * I_sp * g

• Explained:

Δv = ln ( masse initial / masse finale ) X Isp X 9.81

• Example:

Fusée d'un étage de 23 tonnes (avec carburant), 15 tonnes sans carburant et avec moteurs I_sp = 120 s.

Δv = ln ( 23 t / 15 t ) × 120 s × 9.81m/s² = Δv total de 503.2 m/s.

True Δv

1. How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum.
2. Assumption: It takes approximately 1000 m/s of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition.
3. Note: This equation is an guess, approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate."

• Equation for Kerbin Atmospheric Escape:

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}}$

• Simplified:

True Δv = ( ( Δv atm - 1000 ) / Δv atm ) * Δv vac + 1000

• Explained:

True Δv = ( ( Total Δv in atmosphere - 1000 m/s) / Total Δv in atmosphere ) X Total Δv in vacuum + 1000

• Example:

Single Stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum.

Transitional Δv = ( ( 5000 Δv atm - 1000 Δv Required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 1000 Δv Required to escape Kerbin atmosphere = Total Δv of 5800 m/s

See also

• Tutorials
• Terminology
• The Drawing Board: A library of tutorials and other useful information