Difference between revisions of "Cheat sheet"

Revision as of 00:02, 25 January 2019

This page or section is in need of being brought up to date. Please help Kerbal Space Program Wiki by fixing inaccurate or outdated information. This page provides false information about the Δv required in planets with atmospheres. A lot of the information on this page has to be either removed or updated. Due to migration problems, The Δv map cannot be updated.

Kerbal Space Program rocket scientist's cheat sheet: Delta-v maps, equations and more for your reference so you can get from here to there and back again.

Mathematics

Thrust-to-weight ratio (TWR)

→ See also: Thrust-to-weight ratio

This is Newton's Second Law. If the ratio is less than 1 the craft will not lift off the ground. Note that the local gravitational acceleration, which is usually the surface gravity of the body the rocket is starting from, is required.

${\displaystyle {\text{TWR}}={\frac {F_{T}}{m\cdot g}}>1}$

Combined specific impulse (I_sp)

→ See also: Specific impulse

If the I_sp is the same for all engines in a stage, then the I_sp is equal to a single engine. If the I_sp is different for engines in a single stage, then use the following equation:

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

Delta-v (Δv)

Basic calculation

→ See also: Tutorial:Advanced Rocket Design

Basic calculation of a rocket's Δv. Use the atmospheric and vacuum thrust values for atmospheric and vacuum Δv, respectively.

${\displaystyle \Delta {v}=ln\left({\frac {M_{start}}{M_{end}}}\right)\cdot I_{sp}\cdot 9.81{\frac {m}{s^{2}}}}$

True Δv of a stage that crosses from atmosphere to vacuum

Calculation of a rocket stage's Δv, taking into account transitioning from atmosphere to vacuum. Δv_out is the amount of Δv required to leave a body's atmosphere, not reach orbit. This equation is useful to figure out the actual Δv of a stage that transitions from atmosphere to vacuum.

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}}$

Maps

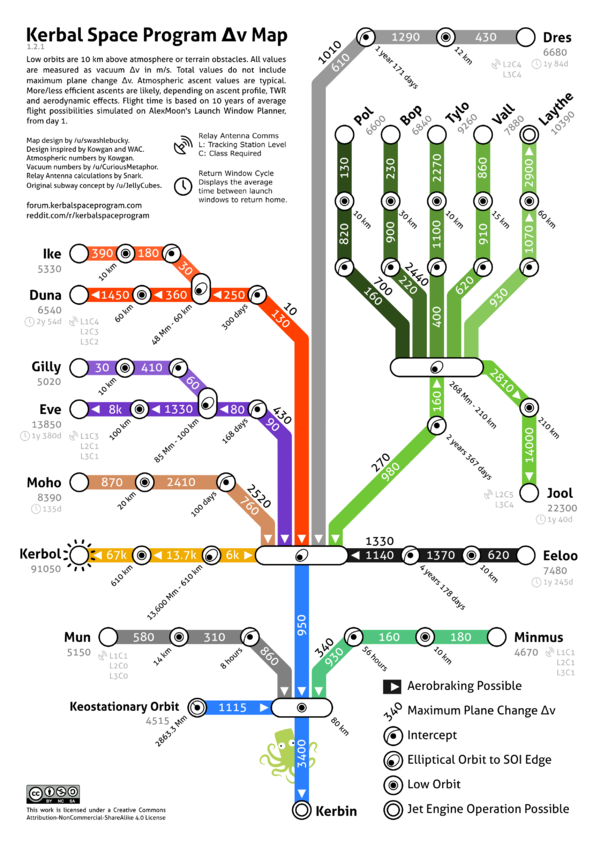
Various fan-made maps showing the Δv required to travel to a certain body.

Subway style Δv map (KSP 1.2.1):

Total Δv values

• http://www.skyrender.net/lp/ksp/system_map.png

Δv change values

• http://i.imgur.com/duY2S.png

Δv with Phase Angles

• http://i.imgur.com/dXT6r7s.png

Precise Total Δv values

• http://i.imgur.com/UUU8yCk.png

WAC's Δv Map for KSP 1.0.4

• http://i.imgur.com/q0gC9H7.png

Maximum Δv chart

This chart is a quick guide to what engine to use for a single stage interplanetary ship. No matter how much fuel you add you will never reach these ΔV without staging to shed mass or using the slingshot maneuver. (These calculations use a full/empty fuel-tank mass ratio of 9 for all engines except those noted.)

ISP(Vac) (s)	Max Δv (m/s)	Engines	Remarks
250	5249	O-10 "Puff"	Monopropellant (max full/empty mass ratio = 8.5)
290	6251	LV-1R "Spider" 24-77 "Twitch"
300	6466	KR-1x2 "Twin-Boar"
305	6574	CR-7 R.A.P.I.E.R. Mk-55 "Thud"
310	6682	LV-T30 "Reliant" RE-M3 "Mainsail"
315	6790	LV-1 "Ant" KS-25 "Vector" KS-25x4 "Mammoth"
320	6898	48-7S "Spark" LV-T45 "Swivel" RE-I5 "Skipper"
340	7329	KR-2L+ "Rhino" T-1 "Dart"
345	7436	LV-909 "Terrier"
350	7544	RE-L10 "Poodle"
800	17244	LV-N "Nerv"
4200	58803	IX-6315 "Dawn"	Xenon (max full/empty mass ratio = 4.167)

(Version: 1.6.1)

Math examples

TWR

• Copy template:

TWR = F / (m * g) > 1

I_sp

1. When I_sp is the same for all engines in a stage, then the I_sp is equal to a single engine. So six 200 I_sp engines still yields only 200 I_sp.
2. When I_sp is different for engines in a single stage, then use the following equation:

• Equation:

${\displaystyle I_{sp}={\frac {(F_{1}+F_{2}+\dots )}{{\frac {F_{1}}{I_{sp1}}}+{\frac {F_{2}}{I_{sp2}}}+\dots }}}$

• Simplified:

I_sp = ( F1 + F2 + ... ) / ( ( F1 / I_sp1 ) + ( F2 / I_sp2 ) + ... )

• Explained:

I_sp = ( Force of thrust of 1st engine + Force of thrust of 2nd engine...and so on... ) / ( ( Force of thrust of 1st engine / I_sp of 1st engine ) + ( Force of thrust of 2nd engine / I_sp of 2nd engine ) + ...and so on... )

• Example:

Two engines, one rated 200 newtons and 120 seconds I_sp ; another engine rated 50 newtons and 200 seconds I_sp.

Isp = (200 newtons + 50 newtons) / ( ( 200 newtons / 120 ) + ( 50 newtons / 200 ) = 130.4347826 seconds I_sp

Δv

1. For atmospheric Δv value, use atmospheric ${\displaystyle I_{sp}}$ values.
2. For vacuum Δv value, use vacuum ${\displaystyle I_{sp}}$ values.
3. Use this equation to figure out the Δv per stage:

• Equation:

${\displaystyle \Delta {v}=ln\left({\frac {M_{start}}{M_{dry}}}\right)\cdot I_{sp}\cdot 9.81{\frac {m}{s^{2}}}}$

• Simplified:

Δv = ln ( Mstart / Mdry ) * I_sp * g

• Explained:

Δv = ln ( starting mass / dry mass ) X Isp X 9.81

• Example:

Single stage rocket that weighs 23 tons when full, 15 tons when fuel is emptied, and engine that outputs 120 seconds I_sp.

Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds I_sp × 9.81m/s² = Total Δv of 503.0152618 m/s

Maximum Δv

Simplified version of the Δv calculation to find the maximum Δv a craft with the given ISP could hope to achieve. This is done by using a magic 0 mass engine and not having a payload.

• Equation:

${\displaystyle \Delta {v}=21.576745349086\cdot I_{sp}}$

• Simplified:

Δv =21.576745349086 * I_sp

• Explained / Examples:

This calculation only uses the mass of the fuel tanks and so the ln ( Mstart / Mdry ) part of the Δv equation has been replaced by a constant as Mstart / Mdry is always 9 (or worse with some fuel tanks) regardless of how many fuel tanks you use.

The following example will use a single stage and fuel tanks in the T-100 to Jumbo 64 range with an engine that outputs 380 seconds I_sp.

Δv = ln ( 18 Tons / 2 Tons ) × 380 seconds I_sp × 9.81m/s² = Maximum Δv of 8199.1632327878 m/s

Δv = 2.1972245773 × 380 seconds I_sp × 9.82m/s² = Maximum Δv of 8199.1632327878 m/s (Replaced the log of mass with a constant as the ratio of total mass to dry mass is constant regardless of the number of tanks used as there is no other mass involved)

Δv = 21.576745349086 × 380 seconds I_sp = Maximum Δv of 8199.1632327878 m/s (Reduced to its most simple form by combining all the constants)

True Δv

1. How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum.
2. Assumption: It takes roughly 2500 m/s of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition (actual value ranges between 2000 m/s and 3400 m/s depending on ascent). Note that, as of KSP 1.3.1, around 3800 m/s of Δv is required to reach an 80km orbit from the KSC.
3. Note: This equation is a guess, an approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate."

• Equation for Kerbin atmospheric escape:

${\displaystyle \Delta {v}_{T}={\frac {\Delta {v}_{atm}-\Delta {v}_{out}}{\Delta {v}_{atm}}}\cdot \Delta {v}_{vac}+\Delta {v}_{out}}$

• Simplified:

True Δv = ( ( Δv atm - 2500 ) / Δv atm ) * Δv vac + 2500

• Explained:

True Δv = ( ( Total Δv in atmosphere - 2500 m/s) / Total Δv in atmosphere ) X Total Δv in vacuum + 2500

• Example:

Single stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum.

Transitional Δv = ( ( 5000 Δv atm - 2500 Δv required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 2500 Δv required to escape Kerbin atmosphere = Total Δv of 5500 m/s

See also

• Tutorials
• Terminology
• The Drawing Board: A library of tutorials and other useful information