Terminology/ja
From Kerbal Space Program Wiki
KSPには軌道や物理に関するたくさんの用語が登場するので素人には少々取っつきにくいところがあります。 また、一般的な用語の代わりに様々な科学用語や略語が使われていたりもします。
このページでは、皆さんが一人前の宇宙飛行士になるうえで必要な用語をリストアップし、簡潔に解説していきます。
数学
- Elliptical/楕円
- 適当に飛ばしていたらほとんど周回軌道は、楕円軌道になる。
- Hyperbolic/双曲線
- 開いた滑らかな曲線。離脱軌道とかは双曲線になる。
- Normal vector/法線ベクトル
- 基準面に対して垂直なベクトル。
- Scalar/スカラー
- 方向を持たないただの値。普通、そのスカラーの次元が何なのかを示す単位が伴う。例えば3 m/sや、3 mや、3 sは、それぞれ速さ、距離、時間の単位が付いているが、方向がないのでスカラーである。
- Vector/ベクトル
- 方向と値がセットになったもの。例えば、方位(方向)と速さが一緒になったvelocity(速度)はベクトル。座標系が何であるか、何次元を考えるかによって、ベクトルの表され方は異なる。<35°, 12>は2次元の極座標ベクトル、<14, 9, -20>は3次元の直交座標ベクトルである。他にも座標系はあるが、この2つが一番よくつかわれる。
- <35°, 12> は、原点から35°(基準軸Xから反時計回りに大きくなる)の角度に向かって伸びる、長さ12の矢印である。(長さが0の場合、角度はない)
- <14, 9, -20> は、原点(<0,0,0>)から、X座標=14、Y座標=9、Z座標=-20の点に向かって伸びる矢印である。
- 直交座標を使う利点は、到着点がはっきり分かる点である。欠点は長さが分かりずらいことである。逆に、極座標は簡単に長さがわかるが、到着点がわかりずらい。
- velocity(速度), acceleration(加速度), force(力)はすべてベクトルである。
3次元座標系では
- 基準点。つまり出発点。
- 3つの基底ベクトル。軸の基本単位と、その方向を定義する。
- その座標系での位置を表す、角度か座標の3つのスカラー。
が必要である。
Orbital Terms
- Apoapsis/遠点
- Periapsis/近点
- Apsis/近点・遠点
- → 参照: “Apoapsis and periapsis” section in Orbit
- 楕円軌道には必ず2つのApsisが存在する。一つはperiapsis (q)といい、周回する天体に最も近い点(軌道の最低点)である。もう一つはapoapsis (Q)といい、periapsisの反対側にあり、天体から最も遠い点(軌道の最高点)である。天体との距離を計算する公式は普通、中心からの距離を考えているが、apsisは表面からの距離を考えているため、それに天体の半径を加算する必要がある。
- Peri~とApo~
- 軌道に関する話では、それが何の天体を周回する軌道かによって「periapsis」と「apoapsis」を少し変えて言う。例えば、Kerbinの周回軌道の場合は~keeや~kerbをつけて、Perikee/Perikerbと言ったりApokee/Apokerbと言ったりする。
- Ascending node/昇交点
- Descending node/降交点
- Orbital node/交点
- 基準面(赤道面や黄動面)と軌道面が交差する点。Ascending nodeは、軌道が北向きに交差する点。Descending nodeは、南向きに交差する点。
- Eccentricity/離心率
- → 参照: “Eccentricity” section in Orbit
- 軌道がどれだけ真円からかけ離れているかを表すスカラーである。
- ecc = 0 → 真円軌道
- 0 < ecc < 1 → 楕円軌道
- ecc = 1 → 放物線軌道(離脱軌道はこれ)
- ecc > 1 → 双曲線軌道(離脱軌道はこれ)
- Inclination/傾斜角
- → 参照: “Inclination” section in Orbit
- 軌道面と基準面の間の角度(例:赤道面に対しinclinationが90°の軌道は極軌道となる)
- Low orbit/低軌道
大気の空気抵抗などの影響を受けず、安定した軌道を保つのに必要最低限な高度の軌道のこと。低軌道は地表から最小の燃料で到達でき、離脱燃焼がどの方向にもできるので、上昇したあと次のランデブー目標(惑星や宇宙船)へ向かうまでの、踏み石として使われる。Kerbinの低軌道はおよそ80km~100kmである。大気のない天体では、理論上、地面より高ければどこでも軌道がとれるが、10km以下だと山や高地に激突する危険性が非常に高い。低軌道でのタイムワープは低く抑えられている。
- Orbital nodes
- Specific points of reference in any orbit such as Apoapsis, Periapsis, intersect points with other orbits etc.
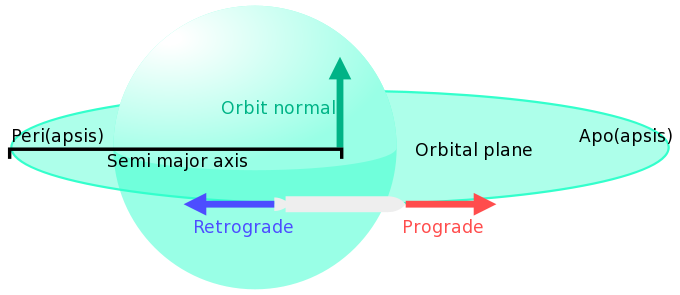
- Orbit normal
- A normal vector of the Orbital Plane. Produced by cross multiplying the ship's velocity and gravity. Since this follows the right hand rule, from a perspective where the ship is orbiting counter-clockwise it will point "up", while for a ship orbiting "clockwise" it will point down. "Up" is also often labeled as "North" or "N+", and in tandem with that "Down" is labeled "Anti-Normal", "South" or "N-".
- Orbital plane
- The imaginary disk described by the path of an orbit around a body (commonly used when describing inclinations).
- Prograde
- The direction in which a ship is traveling along its orbital path. Since orbits are elliptical, it is always tangent to the orbit at the point where the ship is.
- Retrograde
- The reverse of Prograde, backwards along the orbital path.
- Reference plane
- Any plane used as a reference for describing your current orbit. For local orbits around a planet, this is often the equatorial plane. When multiple bodies in a solar system are involved, the ecliptic plane can be used. For intercepting another orbiting body, the orbital plane of the body to be intercepted is used. An orbital plane can be fully described by giving the inclination and the longitude of the ascending node relative to a reference plane.
- Semi-major axis
- → 参照: “Semi-major axis” section in Orbit
- The major-axis is the long axis of an ellipse, and the semi-major axis (a) is half of this. It's the average of the apoapsis (Q) and periapsis (q) computed relative to the center of the body. As both are relative to the body's surface, the radius (R) must be added. All orbits with the same semi-major axis have the same period, regardless of their eccentricity.
- Sidereal period
- The sidereal period is the temporal cycle that it takes an object to make a full orbit, relative to the stars. This is the orbital period in an inertial (non-rotating) frame of reference.
- Sub-orbital
- Describes an orbit where the periapsis is below the surface of a planetary body. If a suborbital path is followed for too long the orbiter will collide with the body being orbited.
- Synodic period
- The synodic period is the temporal interval that it takes for an object to reappear at the same point in relation to two or more other objects, e.g. when the Mun relative to the Kerbol as observed from Kerbin returns to the same illumination phase. The synodic period is the time that elapses between two successive conjunctions with the Kerbol–Kerbin line in the same linear order. The synodic period differs from the sidereal period due to the Kerbin orbiting around the Kerbol.
Ship Orientation
The ship orientation is always relative to a specific object. The terms are usually defined relative to the cockpit.
- Zenith
- Top side of the ship which is usually oriented away from the orbited body. Opposite of nadir.
- Nadir
- Bottom side of the ship which usually oriented towards the orbited body. Opposite of zenith.
- Port(side)
- Left side of the ship. Opposite of starboard.
- Starboard
- Right side of the ship. Opposite of portside.
- Front
- Front side/end of the ship which is usually towards the nose or prograde vector. Opposite of aft.
- Aft
- Back side/end of the ship which is usually housing the primary rockets and facing in retrograde. Opposite of front.
Space Maneuvers
- Atmospheric braking
- → メイン記事: Aerobraking
- Lowering the periapsis so it is inside a planetary atmosphere. This will lead to the vessel being slowed by atmospheric drag. Can lead to atmospheric entry, but also is used to reduce the necessary burn time for significant orbit alterations.
- Lithobraking
- → 参照: Lithobraking on Wikipedia
- An attempted aerobrake using the ground instead of air. Usage of this term implies jokingly that the resulting crash-landing was not in the original plan. An adaptation of the term aerobraking where aero was replaced by the Greek word lithos, meaning “rock” or “stone”.
- Atmospheric entry
- → メイン記事: Atmospheric entry
- Entering atmosphere and using drag to decelerate a vessel to a groundwards trajectory. In real-world science this causes intense heat stress on the object as the vessel requires sufficient speed to not "bounce" back from the atmosphere into space. Currently (0.24.2[outdated]) atmospheric entry is only partially implemented with effects but heat and bounce are not yet implemented, there are mods however which allow parts to overheat. This is usually called re-entry/reentry but in theory only correct in Kerbin's atmosphere; atmospheric entry being the more general term.
- Burn
- firing of the engines, usually to alter trajectory in some way.
- Circularizing
- Reducing an orbit's eccentricity to 0 or close to it. This is usually achieved by a burn close to an apsis.
- Maneuver node
- → メイン記事: Maneuver node
- A planned maneuver in the map view, so as to predict the effect of a burn in advance of performing it.
- Radial-in burn
- A burn performed directly towards the center of a celestial body. It rotates the orbit counter-clockwise until the periapsis passes the center of mass of a celestial body. Opposite of radial-out burn.
- Radial-out burn
- A burn performed directly away from the center of a celestial body. it rotates the orbit clockwise until the periapsis passes the center of mass of a celestial body. Opposite of radial-in burn.
- Radial burn
- → 参照: Maneuver node
- Re-entry
- → 参照: Atmospheric entry
- Retroburn
- A burn performed "backwards", e.g. with the engines facing towards prograde and nose towards retrogade (hence the name). This is a common maneuver to used to lower the periapsos or apoapsis.
Physics
- Acceleration
- Rate of change to the velocity. Acceleration is a vector, measured in "m/s2".
- Ballistic trajectory
- A falling object's trajectory is ballistic. In rocketry it usually indicates that the object in question is only influenced by gravity and does not exert any force (ie. thrust) of its own.
- Delta-v (Δv)
- The change in velocity that has or can be exerted by the spacecraft. This is measured in meters per second (m/s). More mass can reduce the delta-v, while more propulsion can increase it. This makes it a useful value to calculate the effectiveness of launch vehicles. For example, a launch vehicle requires about 4,500 m/s of delta-v to escape Kerbin's atmosphere and achieve a stable orbit.
- Energy
- → 参照: Specific orbital energy on Wikipedia
- The energy of an object in an orbit is the sum of its potential and kinetic energy. The potential energy is and kinetic energy where G is the gravitational constant, M is the mass of the body, m is the mass of the craft, R is the distance from the center of the body and v is the velocity. This results in . This sum stays the same when not thrusting: When approaching periapsis potential energy is transferred into kinetic energy. After passing the periapsis the kinetic energy is converted back into potential energy. When the energy or specific orbital energy is greater than zero the vehicle is on an escape trajectory.
- This is the basic idea behind Kepler's laws of planetary motion, which is what gives rise to KSP's patched conics approximation. An ellipse is the set of all points on a plane such that the sum of the distances to two points - the foci - is some constant. One focus of a Kepler orbit is the centre of mass of the object being orbited; as an object approaches it, it exchanges potential energy for kinetic energy. As the object moves away from this focus - equivalently, if the orbit is elliptical, as the object approaches the other focus - it exchanges kinetic energy for potential energy. If the craft going directly towards or away from the object, the foci coincide with the apsides, where the kinetic (apoapsis) or potential (periapsis) energy is zero. If it's perfectly circular (e.g. the Mun's orbit around Kerbin), the two foci coincide and the locations of the apsides are undefined, since every point of the orbit is an apsis.
- There is also the specific orbital energy () which doesn't require the mass of the craft: , , . All orbits with the same semi-major axis (a) have the same specific orbital energy.
- Escape Velocity
- The velocity needed to escape a given planet's gravity well, as given by where G is the gravitational constant, M is the mass of the planet, and r is the radius of the planet.
- g-force (G)
- A measurement of acceleration as expressed in the sea-level force of Earth's gravity with 1 G being about 9.81 m/s². An object at Earth's surface is accelerated at 1 G. The object weighs twice as much when at 2 G acceleration and is weightless when accelerated with 0 G. In free fall, like in orbit, and without an engine running or an atmosphere applying drag all objects experience no acceleration which can be expressed as 0 G.
- Gravity
- The force exerted by all objects with mass. Very weak. Usually only objects with very high mass - ie. planets, moons - have any noticeable effect. Diminishes with the square of distance from the center of mass. So for an object twice as far, experiences only 1/22 = 1/4 of the gravity.
- Gravity Well
- The area around a planet affected by gravity. Actually extends to infinity, but as gravity decreases quadratically with distance (after twice the distance the gravity is only a quarter), it is only significant within the body's sphere of influence. In fact, in KSP, gravity isn't simulated at all beyond a body's sphere of influence due to its use of the "patched conic approximation".
- Orbit
- → メイン記事: Orbit
- When an object has sufficient tangential velocity (and is outside the atmosphere, so drag won't slow it down) so that it will keep falling "next" to the planet (never touching ground) its trajectory is called an orbit. Stable orbits are elliptical (a circle is an ellipse with zero eccentricity). If the objects tangential speed exceeds escape velocity it's orbit will be either para- or hyperbolic.
- Specific Impulse (Isp)
- → メイン記事: Specific impulse
- The Isp defines how effective a propulsion system is. The higher the Isp the more powerful is the thrust applied to the rocket with the same fuel mass. The Isp is usually given in seconds but actually the physically correct unit is distance per time which is usually given in meters per second or feet per second. To avoid confusion which unit of speed is used, the physical correct Isp (in distance/time) is divided by the surface gravity of Earth (9.81 m/s²). This results in a value given in seconds. To use this Isp in formulas it must to be converted back into distance per time which requires multiplying with the surface gravity of Earth again. As this value is only used to convert between those two units, the specific impulse doesn't change when the gravity changes. It appears that KSP use a value like 9.82 m/s² and thus using a little less fuel.
- As the specific impulse is the ratio of thrust and fuel flow is sometimes given as the unit. This is mathematically another form of because force is the multiplication of mass and acceleration defining . So with the latter being simply only in SI base units.
- Sphere of influence
- → メイン記事: Sphere of influence
- The radius around a celestial body within which its gravity well is non-negligible. Commonly known as SoI/SOI.
- Tangential velocity
- The component of the velocity that is tangential to the trajectory. Instantaneous velocity - velocity when the time of measurement approaches zero - is always tangential to the trajectory.
- Thrust-to-weight ratio
- → 参照: Thrust-to-weight ratio
- The Ratio between the total mass of the vehicle and the available thrust of all propulsion devices of the vehicle/current stage. A TWR greater than 1 means the craft will have enough thrust to accelerate vertically and gain altitude. A TWR below 1 means that the craft won't be able to counteract gravity and drag at low altitudes, although in space it only means that maneuvers will take longer. Because the weight (W) depends on the current gravitational acceleration (g) the TWR depends on which body is currently influencing the craft. The acceleration on the Mun's surface is only 16.6 % of Kerbin's acceleration, so at the surface a TWRKerbin = 1 would be a TWRMun = 6.
- Trajectory
- A trajectory is the path that a moving object follows through space as a function of time.
- Velocity
- Rate of change of the position. It is the combination of speed with the direction. Velocity is a vector, measured in meters per second (m/s).
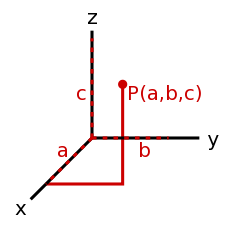
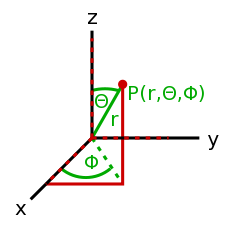










![I_{{sp}}={\frac {T}{{\dot m}}},[I_{{sp}}]={\frac {m}{s}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ff940eef93d9743a07d72ba2bb808e3b0372c36)




