Cheat Sheet/de
Kerbal Space Program Raketentechnikers cheat sheet: Delta-v maps, Gleichungen und mehr als Vorlagen, um immer wieder darauf zurückgreifen zu können.
Mathematik
Schub-Gewichtsverhältnis (TWR)
Template:Siehe auch Das ist Newtons zweites Gesetz. Die Rakete verlässt den Boden nicht, wenn das Verhältnis weniger als 1 ist. Beachte dass die lokale Fallbeschleunigung, welche normalerweise die Anziehungskraft des Körper auf dem die Rakete start ist, benötigt wird.
Kombination spezifischer Impulse(Isp)
Template:Siehe auch Wenn Isp für alle Antriebe in einer Stufe gleich ist, dann ist Isp gleich zu einem einzelnen Antrieb. Wenn Isp unterschiedlich für Antriebe in einer Stufe ist, dann gilt folgende Gleichung:
Delta-v (Δv)
Einfache Berechnung
Template:Siehe auch Benutze für die einfach Berechnung von Δv die Werte für den atmosphärischen- und Vakuumantrieb, für die Δv Werte der Atmosphere und des Vakuums.
Wahre Δv Wert eines Antriebs der von der Atmosphäre zum Vakuum übergeht
| Planet | Δvout |
|---|---|
| Kerbin | 2500 m/s |
| Werte anderer Planeten fehlen | |
Die Berechnung von Δv in einer Raketenstufe, bei Berücksichtigung des Übergans von Atmosphäre zu Vakuum. Δvout ist die Menge an Δv benötigt um die Atmosphäre eines Planetens zu verlassen, nicht um die Umlaufbahn zu erreichen. Diese Gleichung ist sinnvoll um den tatsächlichen Wert von Δv einer Stufe, die von der Atmospähre ins Vakuum übergeht herauszufinden.
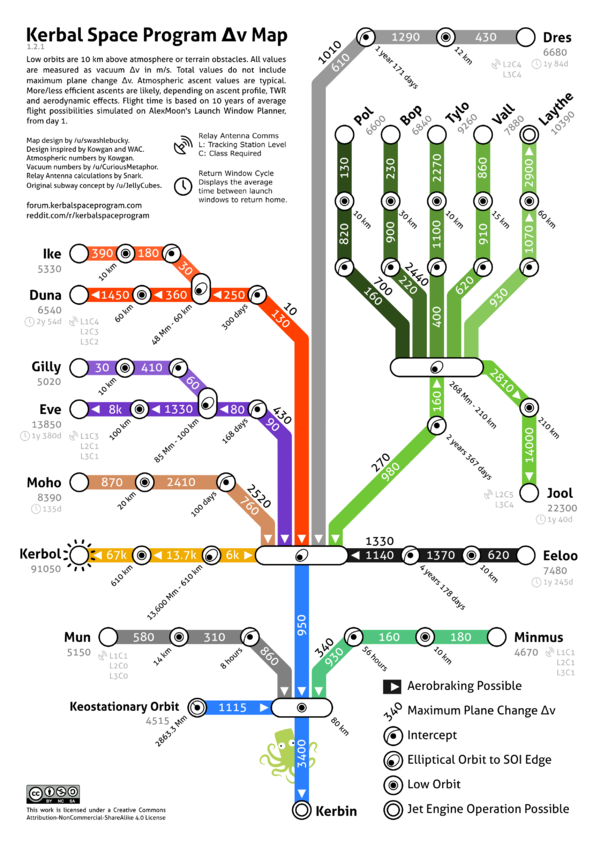
Maps
Verschiedene englischsprachige Maps die den benötigten Wert von Δv angeben, um einen bestimmten Planeten zu erreichen.
U-Bahn ähnliche Δv map (KSP 1.2.1):
Ganze Δv Werte
Δv Änderungswerte
Δv mit Phasen Winkel
Genaue ganze Δv Werte
WAC's Δv Map für KSP 1.0.4
Maximales Δv Tabelle
- Diese Tabelle ist eine kurze Guide, die zeigt welchen Antrieb man für ein Interplanetaren Schiff, mit einer einzelnen Stufe, benutzen soll. Egal wie viel Treibstoff man benutzt, man wird nie diese ΔV Werte erreichen ohne Abstufungen um Masse zu verlieren oder das Slingshot Manöver zu verwenden. (Diese Berechnungen verwenden ein Voll-zu-Leerer Treibstofftank Massenverhältnis von 9 für alle Antriebe, außer die erwähnten.)
ISP(Vac) (s) Maximales Δv (m/s) Antriebe Anmerkungen 250 5249 O-10 "Puff" Monopropellant (Maximales Voll/leer Massenverhältnis = 8.5) 290 6249 LV-1R "Spider"
24-77 "Twitch"300 6464 KR-1x2 "Twin-Boar" 305 6572 CR-7 R.A.P.I.E.R.
Mk-55 "Thud"310 6680 LV-T30 "Reliant"
RE-M3 "Mainsail"315 6787 LV-1 "Ant"
KS-25 "Vector"
KS-25x4 "Mammoth"320 6895 48-7S "Spark"
LV-T45 "Swivel"
RE-I5 "Skipper"340 7326 KR-2L+ "Rhino"
T-1 "Dart"345 7434 LV-909 "Terrier" 350 7542 RE-L10 "Poodle" 800 17238 LV-N "Nerv" 4200 58783 IX-6315 "Dawn" Xenon (Maximales Voll/leer Massenverhältnis = 4.167)
(Version: 1.6.1)
Mathematische Beispiele
TWR
- Vorlage zum kopieren:
- TWR = F / (m * g) > 1
Isp
- Wenn Isp für alle Antriebe in einer Stufe gleich ist, Isp ist das selbe wie von einem einzigen Antrieb. Sechs 200 Isp Antriebe bringen also weiterhin 200 Isp.
- Wenn Isp unterschiedlich ist für die Antriebe einer einzelnen Stufe, benutzte folgende Gleichung:
- Gleichung:
- Vereinfacht:
- Isp = ( F1 + F2 + ... ) / ( ( F1 / Isp1 ) + ( F2 / Isp2 ) + ... )
- Erklärt:
- Isp = (Antriebskraft des ersten Antriebs, Antriebskraft des zweiten Antriebs, und so weiter... ) / ( ( Force of thrust of 1st engine / Isp of 1st engine ) + ( Force of thrust of 2nd engine / Isp of 2nd engine ) + ...and so on... )
- Example:
- Two engines, one rated 200 newtons and 120 seconds Isp ; another engine rated 50 newtons and 200 seconds Isp.
- Isp = (200 newtons + 50 newtons) / ( ( 200 newtons / 120 ) + ( 50 newtons / 200 ) = 130.4347826 seconds Isp
Δv
- For atmospheric Δv value, use atmospheric values.
- For vacuum Δv value, use vacuum values.
- Use this equation to figure out the Δv per stage:
- Equation:
- Simplified:
- Δv = ln ( Mstart / Mdry ) * Isp * g
- Explained:
- Δv = ln ( starting mass / dry mass ) X Isp X 9.81
- Example:
- Single stage rocket that weighs 23 tons when full, 15 tons when fuel is emptied, and engine that outputs 120 seconds Isp.
- Δv = ln ( 23 Tons / 15 Tons ) × 120 seconds Isp × 9.81m/s² = Total Δv of 503.0152618 m/s
Maximum Δv
- Simplified version of the Δv calculation to find the maximum Δv a craft with the given ISP could hope to achieve. This is done by using a magic 0 mass engine and not having a payload.
- Equation:
- Simplified:
- Δv =21.576745349086 * Isp
- Explained / Examples:
- This calculation only uses the mass of the fuel tanks and so the ln ( Mstart / Mdry ) part of the Δv equation has been replaced by a constant as Mstart / Mdry is always 9 (or worse with some fuel tanks) regardless of how many fuel tanks you use.
- The following example will use a single stage and fuel tanks in the T-100 to Jumbo 64 range with an engine that outputs 380 seconds Isp.
- Δv = ln ( 18 Tons / 2 Tons ) × 380 seconds Isp × 9.81m/s² = Maximum Δv of 8199.1632327878 m/s
- Δv = 2.1972245773 × 380 seconds Isp × 9.82m/s² = Maximum Δv of 8199.1632327878 m/s (Replaced the log of mass with a constant as the ratio of total mass to dry mass is constant regardless of the number of tanks used as there is no other mass involved)
- Δv = 21.576745349086 × 380 seconds Isp = Maximum Δv of 8199.1632327878 m/s (Reduced to its most simple form by combining all the constants)
True Δv
- How to calculate the Δv of a rocket stage that transitions from Kerbin atmosphere to vacuum.
- Assumption: It takes roughly 2500 m/s of Δv to escape Kerbin's atmosphere before vacuum Δv values take over for the stage powering the transition (actual value ranges between 2000 m/s and 3400 m/s depending on ascent). Note that, as of KSP 1.3.1, around 3800 m/s of Δv is required to reach an 80km orbit from the KSC.
- Note: This equation is a guess, an approximation, and is not 100% accurate. Per forum user stupid_chris who came up with the equation: "The results will vary a bit depending on your TWR and such, but it should usually be pretty darn accurate."
- Equation for Kerbin atmospheric escape:
- Simplified:
- True Δv = ( ( Δv atm - 2500 ) / Δv atm ) * Δv vac + 2500
- Explained:
- True Δv = ( ( Total Δv in atmosphere - 2500 m/s) / Total Δv in atmosphere ) X Total Δv in vacuum + 2500
- Example:
- Single stage with total atmospheric Δv of 5000 m/s, and rated 6000 Δv in vacuum.
- Transitional Δv = ( ( 5000 Δv atm - 2500 Δv required to escape Kerbin atmosphere ) / 5000 Δv atm ) X 6000 Δv vac + 2500 Δv required to escape Kerbin atmosphere = Total Δv of 5500 m/s