Difference between revisions of "Atmosphere"

From Kerbal Space Program Wiki
Jump to: navigation, search
(Revision of previous change due to lack of complete data)
m
 
(31 intermediate revisions by 17 users not shown)
Line 1: Line 1:
−
{| class="wikitable" style="float:right;margin:0.5em;"
+
[[File:Pressures.svg|thumb|The pressures for all atmospheres]]
−
! colspan="2" | Planets
+
{| class="wikitable float-right"
 +
! colspan="4" | Planets
 +
! style="border-left-width:2px;" colspan="2" | Moons
 
|-
 
|-
 
| style="border-right:0px;" | [[File:TinyEve.png|16px]]
 
| style="border-right:0px;" | [[File:TinyEve.png|16px]]
 
| style="border-left:0px;" | [[Eve]]
 
| style="border-left:0px;" | [[Eve]]
−
|-
 
 
| style="border-right:0px;" | [[File:TinyKerbin.png|16px]]
 
| style="border-right:0px;" | [[File:TinyKerbin.png|16px]]
 
| style="border-left:0px;" | [[Kerbin]]
 
| style="border-left:0px;" | [[Kerbin]]
 +
| style="border-left-width:2px; border-right:0px; vertical-align:top;" rowspan="2" | [[File:TinyLaythe.png|16px]]
 +
| style="border-left:0px; vertical-align:top;" rowspan="2" | [[Laythe]]
 
|-
 
|-
 
| style="border-right:0px;" | [[File:TinyDuna.png|16px]]
 
| style="border-right:0px;" | [[File:TinyDuna.png|16px]]
 
| style="border-left:0px;" | [[Duna]]
 
| style="border-left:0px;" | [[Duna]]
−
|-
 
 
| style="border-right:0px;" | [[File:TinyJool.png|16px]]
 
| style="border-right:0px;" | [[File:TinyJool.png|16px]]
 
| style="border-left:0px;" | [[Jool]]
 
| style="border-left:0px;" | [[Jool]]
−
|-
 
−
! colspan="2" | Moons
 
−
|-
 
−
| style="border-right:0px;" | [[File:TinyLaythe.png|16px]]
 
−
| style="border-left:0px;" | [[Laythe]]
 
 
|}
 
|}
  
−
The '''atmosphere''' of a celestial body slows the movement of any object passing through it, a force known as atmospheric drag (or simply '''drag'''). An atmosphere also allows for aerodynamic lift. The celestial bodies with atmospheres are the planets [[Eve]], [[Kerbin]], [[Duna]] and [[Jool]], as well as [[Laythe]], a moon of Jool.  Only [[Kerbin]] and [[Laythe]] have atmospheres that contain oxygen.
+
The '''atmosphere''' of a celestial body slows the movement of any object passing through it, a force known as atmospheric drag (or simply '''drag'''). An atmosphere also allows for aerodynamic lift. The celestial bodies with atmospheres are the planets [[Eve]], [[Kerbin]], [[Duna]] and [[Jool]], as well as [[Laythe]], a moon of Jool.  Only [[Kerbin]] and [[Laythe]] have atmospheres that contain oxygen and thus produce [[intake air]] for [[jet engine]]s to work, as well as allowing Kerbals to take off their helmets.  
  
−
Atmospheric pressure diminishes exponentially with increasing altitude. An atmosphere's ''scale height'' is the distance over which atmospheric pressure changes as a factor of ''e'', or 2.718. For example, Kerbin's atmosphere has a scale height of 5000 m, meaning the atmospheric pressure at altitude ''n'' is 2.718 times
+
Atmospheres allow [[aerobraking]] and easier landing. However, an atmosphere makes taking off from a planet more difficult and increases the minimum stable orbit altitude.
−
greater than the pressure at altitude ''n'' + 5000.
 
  
−
Atmospheres vary in temperature, though this has no bearing on gameplay.
+
== Physical quantities ==
 +
Atmospheres have a '''pressure''' that varies in an exponential way with the increasing altitude:
 +
: <math>p = p_0 \cdot e^\frac{-altitude}{H}</math>
  
−
Atmosphere allows [[aerobraking]] and easier landing. When atmosphere contains oxygen, it allows jet engines to work. However, atmosphere makes taking off from a planet more difficult and increases a stable orbit altitude.
+
where ''p<sub>0</sub>'' is the atmosphere's pressure (Pa) at altitude 0, and ''H'' is the scale height (m).
  
−
== Drag ==
+
The ''scale height'' of an atmosphere define at which rate the pressure drops with altitude. In the case of Kerbin's atmosphere, the scale height is about 5600m and means that the atmospheric pressure will be 2.718 times smaller each time you go 5600m higher.
−
[[File:Ml16-XL_parachute.JPG|thumb|right|A Mk1-2 pod with a Mk16-XL parachute being slowed by drag in Kerbin's atmosphere.]]
 
  
−
In the game, the force of atmospheric drag (''F<sub>D</sub>'') is modeled as follows:<ref>http://forum.kerbalspaceprogram.com/showthread.php/5235-Atmospheric-drag?p=88804&viewfull=1#post88804</ref>
+
Atmospheres also vary in '''temperature'''. Though this has little effect on gameplay, it affects the atmospheric density and the speed of sound both used in drag calculations. With the [[w:Ideal_gas_law|Ideal gas law]] the density (''&rho;'') in kg/m<sup>3</sup> is calculated with the equation:
  
−
: <math>F_D = 0.5\, \rho\, v^2\, m\, d\, A</math>
+
<!-- Bypassing the fact that parsing math equations dont work. Replace with the math attributes when they will work.-->
 +
[[File:DensityEq.png]]
 +
<!--: <math>\rho = \frac{p}{R \cdot T}</math>-->
  
−
where ''&rho;'' is the atmospheric density (kg/m<sup>3</sup>), ''v'' is the ship's velocity (m/s), ''m'' is the ship's mass (kg), ''d'' is the coefficient of drag (dimensionless), and ''A'' is the [[w:cross section (geometry)|cross-sectional area]] (m<sup>2</sup>).
+
where ''R'' is the [[w:Gas_constant#Specific_gas_constant|specific gas constant]] equal to 287.053 J/kg-K.
  
−
Note that the ''m'' term is not present in the [[w:drag equation|real-word drag equation]]. In the game, this causes acceleration due to drag (''a = F<sub>D</sub> / m'') to be unaffected by a ship's mass. (It also causes the units of the drag equation to have an extra "kg" term.)
+
The speed of sound (c) is calculated with:
  
−
''&rho;'' can be derived from atmospheric pressure (''p'' of unit ''atm''), which is a function of the atmosphere's pressure at altitude 0 (''p<sub>0</sub>'') and scale height (''H''):
+
<!-- Bypassing the fact that parsing math equations dont work. Replace with the math attributes when they will work.-->
 +
[[File:SpeedOfSoundEq.png]]
 +
<!--: <math>c = \sqrt{1.4 \cdot R \cdot T}</math>-->
  
−
: <math>p = p_0 \cdot e^{-altitude / H}</math>
+
Note that for Kerbin atmosphere, the pressure and temperature are modeled to match Earth atmosphere by using  [[w:U.S._Standard_Atmosphere|U.S. Standard Atmosphere]] (USSA) equations (see [[Kerbin#Atmosphere|Kerbin atmosphere]]).
  
−
: <math>\rho = p \cdot 1.2002 \cdot 0.008</math>
 
−
<!--    rho = p * FlightGlobals.getAtmDensity(1.0) * FlightGlobals.DragMultiplier -->
 
  
−
The 1.2002 value can be derived from the [[w:Air_density|ideal gas law]] (assuming that T is always 293.15K as it is inconclusive if Temperature is important) and the factor of 0.008 is just the way the Kerbal universe works. This yields
+
== Drag ==
 +
[[File:Mk16-XL Parachute.jpg|thumb|right|A Mk1-2 pod with a Mk16-XL parachute being slowed by drag in Kerbin's atmosphere.]]
 +
In the game, the force of atmospheric '''drag''' is dependent on the shape of a part and which of the part's attachment nodes are in use. For example, nose cones reduce drag on the part to which they are attached. A debug-mode option allows you to see the exact drag force on a given part by right-clicking on it.
  
−
: <math>\rho ~= p \cdot \frac{101 \text{kPa}}{1 \text{atm} \cdot 287.058 \text{J/(kg·K)} \cdot 293.15 \text{K}} \cdot 0.008</math>
+
Generally, the drag works with the following equation:
 +
: <math>F_D = 0.5\, \rho\, v^2\, d\, A</math>
  
 +
where ''&rho;'' is the atmospheric density (kg/m<sup>3</sup>), ''v'' is the ship's velocity (m/s), ''d'' is the coefficient of drag (dimensionless), and ''A'' is the [[w:cross section (geometry)|cross-sectional area]] (m<sup>2</sup>).
  
−
where p here is in units atm. The coefficient of drag (''d'') is calculated as the mass-weighted average of the max_drag values of all [[parts]] on the ship. For most ships without deployed parachutes, ''d'' will be very near 0.2, since this is the max_drag value of the vast majority of parts.
 
  
−
As an example, the coefficient of drag for a craft consisting simply of a [[Mk1-2 Command Pod]] (mass 4, drag 0.2) and a deployed [[Mk16-XL Parachute]] (mass 0.3, drag 500) is:
+
== Atmospheric height ==
−
 
+
The '''atmospheric height''' depends on the scale height of the celestial body and is where 0.000001<sup>th</sup> (0.0001%) of the surface pressure remains. Therefore, the atmospheric pressure at the edge of the atmosphere is relative; for example a craft in orbit around Jool can have a lower orbit (relative to the surface) because the surface pressure is higher.
−
: <math>\frac{4 \cdot 0.2 + 0.3 \cdot 500}{4 + 0.3} = 35.07</math>
+
:<math>alt_{\text{atmospheric height}} = -ln\left(10^{-6}\right) \cdot \text{scale height}</math>
 +
:<math>p_{\text{atmospheric height}} = p_0 \cdot 10^{-6}</math>
 +
To calculate the atmospheric heights of other celestial bodies:
 +
:<math>alt_{\text{atmospheric height (real)}} = -ln\left(\frac{10^{-6}}{p_0}\right) \cdot \text{scale height}</math>
  
−
Note that the game does not calculate the ship's cross-sectional area (''A'') and assumes a value of 1 instead. This means the net force of drag on a spacecraft is unaffected by the width or orientation of a spacecraft, even if the spacecraft has very large wings. (Wings do affect the force of lift, however.)
 
  
 
== Terminal velocity ==
 
== Terminal velocity ==
−
The [[w:terminal velocity|terminal velocity]] of an object falling through an atmosphere is the velocity at which the force of gravity is equal to the force of drag. Terminal velocity changes as a function of altitude. Given enough time, an object falling into the atmosphere will slow to terminal velocity and then remain at terminal velocity for the rest of its fall.
+
{{See also||{{Wikipedia|terminal velocity}}}}
 +
The '''terminal velocity''' of an object falling through an atmosphere is the velocity at which the force of gravity is equal to the force of drag. Terminal velocity changes as a function of altitude. Given enough time, an object falling into the atmosphere will slow to terminal velocity and then remain at terminal velocity for the rest of its fall.
  
 
Terminal velocity is important because:
 
Terminal velocity is important because:
Line 69: Line 74:
 
The force of gravity (''F<sub>G</sub>'') is:
 
The force of gravity (''F<sub>G</sub>'') is:
  
−
: <math>F_G = m\, a = m\, \frac{GM}{r^2}</math>
+
: <math>F_G = m \cdot a = m \cdot \frac{GM}{r^2}</math>
  
 
where ''m'' is still the ship's mass, ''G'' is the [[Template:G|gravitational constant]], ''M'' is the mass of the planet, and ''r'' is the distance from the ''center'' of the planet to the falling object.
 
where ''m'' is still the ship's mass, ''G'' is the [[Template:G|gravitational constant]], ''M'' is the mass of the planet, and ''r'' is the distance from the ''center'' of the planet to the falling object.
  
−
To find terminal velocity, we set ''F<sub>G</sub>'' equal to ''F<sub>D</sub>'':
+
The terminal velocity can be found by finding for what speed ''F<sub>G</sub>'' is equal to ''F<sub>D</sub>''.
−
 
 
−
: <math>m\, \frac{GM}{r^2} = 0.5\, \rho\, v^2\, m\, d\, A</math>
 
−
 
 
−
: <math>\frac{GM}{r^2}    = 0.5\, \rho\, v^2\, d\, A</math>
 
−
 
 
−
: <math>v = v_T = \sqrt{\frac{2\, GM}{r^2\, \rho\, d\, A}}</math>
 
−
 
 
−
Assuming ''d'' is 0.2 (which is a good approximation, provided parachutes are not in use) and given that ''A'' is 1, this simplifies to:
 
−
 
 
−
: <math>v_T = \sqrt{\frac{10\, GM}{r^2\, \rho}}</math>
 
−
 
 
−
For the Mk16 pod and parachute example pictured above, the drag coefficient is 35.07, so its terminal velocity at sea level on Kerbin (which is 600 km from Kerbin's center) is:
 
−
 
 
−
: <math>v_T = \sqrt{\frac{2\, GM}{r^2\, \rho \cdot 35.07}}</math>
 
−
 
 
−
: <math>\rho = 1 \cdot e^{-0/5000} \cdot 1.2002 \cdot 0.008</math>
 
−
 
 
−
: <math>v_T = \sqrt{\frac{2 \cdot 6.674 \cdot 10^{-11} \cdot 5.2915793 \cdot 10^{22}}{600000^2 \cdot 1.2002 \cdot 0.008 \cdot 35.07}} = 7.63 \operatorname{m/s}</math>
 
  
 
=== Examples ===
 
=== Examples ===
 +
The terminal velocity for an given imaginary body depends from the altitude on the different celestial bodies.
 
{| class="wikitable"
 
{| class="wikitable"
 
!rowspan=2 valign=bottom| Altitude (m) ||colspan=6| v<sub>T</sub> (m/s)
 
!rowspan=2 valign=bottom| Altitude (m) ||colspan=6| v<sub>T</sub> (m/s)
Line 109: Line 97:
  
 
== On-rails physics ==
 
== On-rails physics ==
−
If a ship is "on rails" (meaning it's further than 2.25&nbsp;km from the actively-controlled ship) and its orbit passes through a planet's atmosphere, one of two things will happen based on atmospheric pressure at the ship's altitude:
+
A ship is "'''on rails'''" when it's no longer the primary focus of the simulation, which occurs when it's further than 2.25&nbsp;km from the actively-controlled ship. If such a ship have its orbit passing through a planet's atmosphere, one of two things will happen based on atmospheric pressure at the ship's altitude:
  
 
* below 0.01&nbsp;atm: no atmospheric drag will occur &mdash; the ship will be completely unaffected
 
* below 0.01&nbsp;atm: no atmospheric drag will occur &mdash; the ship will be completely unaffected
Line 119: Line 107:
 
! Body || Altitude (m)
 
! Body || Altitude (m)
 
|-
 
|-
−
| [[Eve]]    ||align="right"| {{Formatnum|{{PressureAltitude|pressure=0.01|body=Eve}}}}
+
| [[Eve]]    ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Eve}}}}
 
|-
 
|-
−
| [[Kerbin]] ||align="right"| {{Formatnum|{{PressureAltitude|pressure=0.01|body=Kerbin}}}}
+
| [[Kerbin]] ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Kerbin}}}}
 
|-
 
|-
−
| [[Duna]]  ||align="right"| {{Formatnum|{{PressureAltitude|pressure=0.01|body=Duna}}}}
+
| [[Duna]]  ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Duna}}}}
 
|-
 
|-
−
| [[Jool]]  ||align="right"| {{Formatnum|{{PressureAltitude|pressure=0.01|body=Jool}}}}
+
| [[Jool]]  ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Jool}}}}
 
|-
 
|-
−
| [[Laythe]] ||align="right"| {{Formatnum|{{PressureAltitude|pressure=0.01|body=Laythe}}}}
+
| [[Laythe]] ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Laythe}}}}
 
|}
 
|}
  
−
== Atmospheric height ==
+
== See also ==
−
The atmospheric height depend on the scale height of the celestial body and is where 0.000001<sup>th</sup> (0.0001&nbsp;%) of the surface pressure is remaining so the atmospheric pressure at the border isn't constant. Technically a craft in Jool's orbit can get lower into the atmosphere (or the atmosphere starts from a higher pressure).
+
* [[Atmospheric entry]]
−
:<math>alt_{\text{atmospheric height}} = -ln\left(10^{-6}\right) \cdot \text{scale height}</math>
 
−
:<math>p_{\text{atmospheric height}} = p_0 \cdot 10^{-6}</math>
 
−
Kerbin's atmosphere ends at 0.000001&nbsp;atm and to calculate where the other celestial bodies should have the atmospheric height:
 
−
:<math>alt_{\text{atmospheric height (real)}} = -ln\left(\frac{10^{-6}}{p_0}\right) \cdot \text{scale height}</math>
 
  
 
== Notes ==
 
== Notes ==
 
<references />
 
<references />
 +
 +
[[Category:Celestials]]

Latest revision as of 02:09, 4 November 2022

The pressures for all atmospheres
Planets Moons
TinyEve.png Eve TinyKerbin.png Kerbin TinyLaythe.png Laythe
TinyDuna.png Duna TinyJool.png Jool

The atmosphere of a celestial body slows the movement of any object passing through it, a force known as atmospheric drag (or simply drag). An atmosphere also allows for aerodynamic lift. The celestial bodies with atmospheres are the planets Eve, Kerbin, Duna and Jool, as well as Laythe, a moon of Jool. Only Kerbin and Laythe have atmospheres that contain oxygen and thus produce intake air for jet engines to work, as well as allowing Kerbals to take off their helmets.

Atmospheres allow aerobraking and easier landing. However, an atmosphere makes taking off from a planet more difficult and increases the minimum stable orbit altitude.

Physical quantities

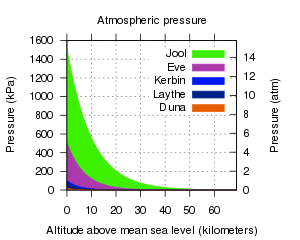
Atmospheres have a pressure that varies in an exponential way with the increasing altitude:

where p0 is the atmosphere's pressure (Pa) at altitude 0, and H is the scale height (m).

The scale height of an atmosphere define at which rate the pressure drops with altitude. In the case of Kerbin's atmosphere, the scale height is about 5600m and means that the atmospheric pressure will be 2.718 times smaller each time you go 5600m higher.

Atmospheres also vary in temperature. Though this has little effect on gameplay, it affects the atmospheric density and the speed of sound both used in drag calculations. With the Ideal gas law the density (ρ) in kg/m3 is calculated with the equation:

DensityEq.png

where R is the specific gas constant equal to 287.053 J/kg-K.

The speed of sound (c) is calculated with:

SpeedOfSoundEq.png

Note that for Kerbin atmosphere, the pressure and temperature are modeled to match Earth atmosphere by using U.S. Standard Atmosphere (USSA) equations (see Kerbin atmosphere).


Drag

A Mk1-2 pod with a Mk16-XL parachute being slowed by drag in Kerbin's atmosphere.

In the game, the force of atmospheric drag is dependent on the shape of a part and which of the part's attachment nodes are in use. For example, nose cones reduce drag on the part to which they are attached. A debug-mode option allows you to see the exact drag force on a given part by right-clicking on it.

Generally, the drag works with the following equation:

where ρ is the atmospheric density (kg/m3), v is the ship's velocity (m/s), d is the coefficient of drag (dimensionless), and A is the cross-sectional area (m2).


Atmospheric height

The atmospheric height depends on the scale height of the celestial body and is where 0.000001th (0.0001%) of the surface pressure remains. Therefore, the atmospheric pressure at the edge of the atmosphere is relative; for example a craft in orbit around Jool can have a lower orbit (relative to the surface) because the surface pressure is higher.

To calculate the atmospheric heights of other celestial bodies:


Terminal velocity

→ See also: terminal velocity on Wikipedia

The terminal velocity of an object falling through an atmosphere is the velocity at which the force of gravity is equal to the force of drag. Terminal velocity changes as a function of altitude. Given enough time, an object falling into the atmosphere will slow to terminal velocity and then remain at terminal velocity for the rest of its fall.

Terminal velocity is important because:

  1. It describes the amount of velocity which a spacecraft must burn away when it is close to the ground.
  2. It represents the speed at which a ship should be traveling upward during a fuel-optimal ascent.

The force of gravity (FG) is:

where m is still the ship's mass, G is the gravitational constant, M is the mass of the planet, and r is the distance from the center of the planet to the falling object.

The terminal velocity can be found by finding for what speed FG is equal to FD.

Examples

The terminal velocity for an given imaginary body depends from the altitude on the different celestial bodies.

Altitude (m) vT (m/s)
Eve Kerbin Duna Jool Laythe
0 58.385 100.13 212.41 23.124 115.62
100 58.783 101.01 214.21 23.162 116.32
1000 62.494 109.30 231.16 23.508 122.83
10000 115.27 240.52 495.18 27.272 211.77

On-rails physics

A ship is "on rails" when it's no longer the primary focus of the simulation, which occurs when it's further than 2.25 km from the actively-controlled ship. If such a ship have its orbit passing through a planet's atmosphere, one of two things will happen based on atmospheric pressure at the ship's altitude:

  • below 0.01 atm: no atmospheric drag will occur — the ship will be completely unaffected
  • 0.01 atm or above: the ship will disappear

The following table gives the altitude of this 0.01 atm threshold for each celestial body with an atmosphere:

Body Altitude (m)
Eve 44 745
Kerbin 25 789
Duna 10 814
Jool 219 397
Laythe 32 755

See also

Notes

Retrieved from "https://wiki.kerbalspaceprogram.com/index.php?title=Atmosphere&oldid=104138"