Difference between revisions of "Terminology/ja"
From Kerbal Space Program Wiki
(→マニューバ) |
m |
||
| (16 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{DISPLAYTITLE:Terminology|用語}} | ||
KSPには軌道や物理に関するたくさんの用語が登場するので素人には少々取っつきにくいところがあります。 | KSPには軌道や物理に関するたくさんの用語が登場するので素人には少々取っつきにくいところがあります。 | ||
また、一般的な用語の代わりに様々な科学用語や略語が使われていたりもします。 | また、一般的な用語の代わりに様々な科学用語や略語が使われていたりもします。 | ||
| Line 11: | Line 12: | ||
;Elliptical/[[w:ja:楕円|楕円]] | ;Elliptical/[[w:ja:楕円|楕円]] | ||
| − | : | + | :周回軌道はふつう楕円軌道である。 |
;Hyperbolic/[[w:ja:双曲線|双曲線]] | ;Hyperbolic/[[w:ja:双曲線|双曲線]] | ||
| − | : | + | :開いた滑らかな曲線。離脱軌道などは双曲線になる。 |
;Normal vector/[[w:ja:法線ベクトル|法線ベクトル]] | ;Normal vector/[[w:ja:法線ベクトル|法線ベクトル]] | ||
:基準面に対して垂直なベクトル。 | :基準面に対して垂直なベクトル。 | ||
;Scalar/[[w:ja:スカラー_(物理学)|スカラー]] | ;Scalar/[[w:ja:スカラー_(物理学)|スカラー]] | ||
| − | : | + | :方向を持たないただの値。普通そのスカラーの次元が何なのかを示す単位が伴う。例えば3 m/sや、3 mや、3 sは、それぞれ速さ、距離、時間の単位が付いているが、方向がないのでスカラーである。 |
;Vector/[[w:ja:空間ベクトル|ベクトル]] | ;Vector/[[w:ja:空間ベクトル|ベクトル]] | ||
| − | : | + | :方向と値がセットになったもの。例えば、方位(方向)と速さが一緒になった「速度(velocity)」はベクトル。座標系が何であるか、何次元を考えるかによって、ベクトルの表され方は異なる。 <35°, 12>は2次元の極座標ベクトル、<14, 9, -20>は3次元の直交座標ベクトルである。他にも座標系はあるが、この2つが一番よくつかわれる。 |
:<35°, 12> は、原点から35°(基準軸Xから反時計回りに大きくなる)の角度に向かって伸びる、長さ12の矢印である。(長さが0の場合、角度はない) | :<35°, 12> は、原点から35°(基準軸Xから反時計回りに大きくなる)の角度に向かって伸びる、長さ12の矢印である。(長さが0の場合、角度はない) | ||
| Line 35: | Line 36: | ||
が必要である。 | が必要である。 | ||
| − | == 軌道 == | + | == 軌道の種類 == |
| + | ;Trajectory / 軌道 | ||
| + | :軌道とは時間に従って物体が宇宙を進んでいく経路である。 | ||
| + | |||
| + | ;Ballistic trajectory / 弾道 | ||
| + | :落ちている物体の軌道は弾道である。ロケット工学では、重力以外なんの力(推力等)も働いていない物体の軌道をいう。 | ||
| + | |||
| + | ;Orbit / 周回軌道 | ||
| + | {{Main article|Orbit}} | ||
| + | :充分な接線速度を持つ(かつ大気圏外にあり空気抵抗を受けない)と、物体は常に惑星の「隣り」に落ちることを繰り返す(地面に落ちない)。このような軌道を周回軌道という。安定した周回軌道は楕円(円は離心率ゼロの楕円)である。接線速度が脱出速度を超えると周回軌道は放物線もしくは双曲線になる。 | ||
| + | |||
| + | ;<span id="suborb">Sub-orbital / 準軌道</span> | ||
| + | :periapsisが天体の表面よりも低い軌道のこと。つまり、いったん宇宙に飛び出すが、再び地表に戻ってくるような軌道。 | ||
| + | |||
| + | == 軌道の要素 == | ||
[[File:Orbit.svg|thumb|upright=2.25|主な軌道パラメーター]] | [[File:Orbit.svg|thumb|upright=2.25|主な軌道パラメーター]] | ||
| − | + | ;Apsis / [[w:ja:近点・遠点|極点]] | |
| − | |||
| − | ;Apsis/近点・遠点 | ||
{{See also|Orbit|section=Apoapsis and periapsis}} | {{See also|Orbit|section=Apoapsis and periapsis}} | ||
| − | : | + | :楕円軌道には次の2つのapsisが必ず存在する。 |
| − | + | :*'''Apoapsis/遠点''':天体から最も遠い点(軌道の最高点)。マップでは'''AP'''と表示される。アポジともいう。 | |
| − | : | + | :*'''Periapsis/近点''':天体から最も近い点(軌道の最低点)。マップでは'''PE'''と表示される。ペリジともいう。 |
| − | ; | + | |
| − | ; | + | :Apsisは楕円の長軸上に存在し、互いに天体を挟んで反対に位置する。 |
| − | ; | + | :天体との距離を計算する公式は中心点からの距離を使うが、apsisは表面からの距離なので、それに天体の半径分を加算する必要がある。 |
| − | : | + | |
| − | ; | + | :*'''Peri~とApo~''':特定の天体のApsisであることを強調したいとき、後ろに天体名をもじってつける。例えばKerbinの周回軌道の場合は~keeや~kerbをつけて、Perikee/Perikerbと言ったりApokee/Apokerbと言ったりする。 |
| + | |||
| + | ;Orbital plane / 軌道面 | ||
| + | :天体を回る軌道が描く仮想の円盤。 | ||
| + | |||
| + | ;Reference plane / 基準面 | ||
| + | :現在の軌道を記述するために基準とするあらゆる平面のこと。惑星を周回する軌道の場合、赤道面が基準面になる。太陽系において複数の天体がからむ場合、黄道面が基準面になる。他の物体をインターセプトする場合、その物体の軌道が基準面になる。基準面に対する'''inclination'''と'''ascending node'''の経度を知ることで、軌道面を完全に記述することができる。 | ||
| + | |||
| + | ;Inclination / [[w:ja:軌道傾斜角|傾斜角]] | ||
| + | {{See also|Orbit|section=Inclination}} | ||
| + | :軌道面と基準面の間の角度(例:赤道面に対しinclinationが90°の軌道は極軌道となる) | ||
| + | |||
| + | ;Orbital node / [[w:ja:交点_(天文)|交点]] | ||
| + | :基準面と軌道面が交差する点。実際の天文学的定義とは異なるがゲーム内ではApsisもこれに含まれる。 | ||
| + | :*'''Ascending node/昇交点''':軌道が北向きに交差する点。マップでは'''AN'''と表示される。 | ||
| + | :*'''Descending node/降交点''':軌道が南向きに交差する点。マップでは'''DN'''と表示される。 | ||
| + | |||
| + | ;Eccentricity / [[w:ja:軌道離心率|離心率]] | ||
{{See also|Orbit|section=Eccentricity}} | {{See also|Orbit|section=Eccentricity}} | ||
| − | |||
:軌道がどれだけ真円からかけ離れているかを表すスカラーである。 | :軌道がどれだけ真円からかけ離れているかを表すスカラーである。 | ||
| + | :<math>\text{ecc} = 1 - \frac{2}{\frac{Ap}{Pe}+1}</math> | ||
:* ecc = 0 → 真円軌道 | :* ecc = 0 → 真円軌道 | ||
:* 0 < ecc < 1 → 楕円軌道 | :* 0 < ecc < 1 → 楕円軌道 | ||
:* ecc = 1 → 放物線軌道(離脱軌道はこれ) | :* ecc = 1 → 放物線軌道(離脱軌道はこれ) | ||
:* ecc > 1 → 双曲線軌道(離脱軌道はこれ) | :* ecc > 1 → 双曲線軌道(離脱軌道はこれ) | ||
| − | + | ||
| − | + | ;Semi-major axis / [[w:ja:軌道長半径|軌道長半径]] | |
| − | |||
| − | ; | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{See also|Orbit|section=Semi-major axis}} | {{See also|Orbit|section=Semi-major axis}} | ||
| − | :楕円の長軸をmajor-axisといい、sami-major axis(<tt>a</tt>)はその半径である。apoapsis (<tt> | + | :<math>\text{a} = \text{R} + \frac{Ap+Pe}{2}</math> |
| − | ;<span id="sidereal period">Sidereal period/恒星周期</span> | + | :楕円の長軸をmajor-axisといい、sami-major axis(<tt>a</tt>)はその半径である。apoapsis (<tt>Ap</tt>) とperiapsis (<tt>Pe</tt>)の平均から求まる。もちろん、これに天体の半径(<tt>R</tt>)を加算しなければならない。軌道長半径が同じ軌道は、離心率によらず、必ず同じ周期になる。 |
| + | |||
| + | ;<span id="sidereal period">Sidereal period / 恒星周期</span> | ||
:恒星周期は、物体が恒星の周りを一周するのにかかる時間である。これは慣性系(非回転座標系)における公転周期である。 | :恒星周期は、物体が恒星の周りを一周するのにかかる時間である。これは慣性系(非回転座標系)における公転周期である。 | ||
| − | + | ||
| − | + | ;<span id="synodic period">Synodic period / 会合周期</span> | |
| − | ;<span id="synodic period">Synodic period/会合周期</span> | ||
:会合周期とは、2つ以上の物体の関係において、ある物体が再び同じ位置に戻るまでにかかる時間。例えば、[[Kerbol/ja|Kerbol]]から観測したとき、[[Kerbin/ja|Kerbin]]に対して[[Mun/ja|Mun]]が再び同じ満ち欠けに見える位置に来るまでの時間。Kerbol-Kerbinラインを考えたとき、再びそのラインに交わるまでの時間と同じ。公転周期の一つだが、Kerbolを周回するKerbinから観測しているため、恒星周期とは異なる。 | :会合周期とは、2つ以上の物体の関係において、ある物体が再び同じ位置に戻るまでにかかる時間。例えば、[[Kerbol/ja|Kerbol]]から観測したとき、[[Kerbin/ja|Kerbin]]に対して[[Mun/ja|Mun]]が再び同じ満ち欠けに見える位置に来るまでの時間。Kerbol-Kerbinラインを考えたとき、再びそのラインに交わるまでの時間と同じ。公転周期の一つだが、Kerbolを周回するKerbinから観測しているため、恒星周期とは異なる。 | ||
| − | == | + | ;Low orbit / [[w:ja:低軌道|低軌道]] |
| + | :大気の空気抵抗などの影響を受けず、安定した軌道を保つのに必要最低限な高度の周回軌道のこと。低軌道は地表から最小の燃料で到達でき、離脱燃焼がどの方向にもできるので、上昇したあと次のランデブー目標(惑星や宇宙船)へ向かうまでの、踏み石として使われる。[[Kerbin/ja|Kerbin]]の低軌道はおよそ80km~100kmである。大気のない天体では、理論上、地面より高ければどこでも軌道がとれるが、10km以下だと山や高地に激突する危険性が非常に高い。低軌道での[[time warp/ja|タイムワープ]]は低く抑えられている。 | ||
| + | |||
| + | == 方向 == | ||
| + | === 軌道における方向 === | ||
| + | ;Radial-in/ラジアル・イン | ||
| + | :天体の中心に向かう方向。radial-outの反対。 | ||
| + | ;Radial-out/ラジアル・アウト | ||
| + | :天体の中心から離れる方向。radial-inの反対。 | ||
| + | ;Orbit normal/オービット・ノーマル | ||
| + | :軌道面の法線ベクトル。船の速度と重力の外積にあたる。右手の法則において中指を重力方向、人差し指を速度方向としたときの親指の方向がOrbital Normal。船が反時計回りに回っているときは、「Up」となり、時計回りに回っているときは「Down」となる。「Up」の代わりに「North」や「N+」と書くことがある。同様に「Down」を「Anti-Normal」「South」「N-」と書くことがある。 | ||
| + | ;Prograde/順行 | ||
| + | :船が軌道に沿って進んでいる方向。軌道はふつう楕円なので、常に、船がいる点における接線となる。 | ||
| + | ;Retrograde/逆行 | ||
| + | :Progradeの反対方向。軌道に沿って後ろ向き。 | ||
| + | |||
| + | === 船における方向 === | ||
;Zenith /天頂 | ;Zenith /天頂 | ||
| − | : | + | :船の天井側。普通、天体から離れていく方向。Radial-outと同じ。Nadirの反対。 |
;Nadir /天底 | ;Nadir /天底 | ||
| − | : | + | :船の床側。普通、天体に向かっていく方向。Radial-inと同じ。Zenithの反対。 |
;Port(side) /左舷 | ;Port(side) /左舷 | ||
:船の左側。starboardの反対。 | :船の左側。starboardの反対。 | ||
| Line 99: | Line 129: | ||
== マニューバ == | == マニューバ == | ||
| − | ;Atmospheric braking / | + | ;<span id="aerobraking">Atmospheric braking / エアロブレーキ</span> |
| − | {{Main article|Aerobraking}} | + | {{Main article|Aerobraking/ja|エアロブレーキング}} |
| − | : | + | :periapsisを惑星の大気を通るように下げること。こうすることによって空気抵抗が船のスピードを低下させる。そのまま大気圏突入に繋げることもできるし、燃料を使わずに軌道を大きく変えることができる。空力ブレーキ、大気ブレーキともいう。 |
| − | ;Lithobraking / | + | |
| − | {{ | + | :;Lithobraking / リトブレーキ |
| − | : | + | :{{see also||{{Wikipedia|Lithobraking}}}} |
| − | ; | + | ::空気の代わりに地面を使ってブレーキを行うこと。エアロブレーキの「エアロ」をギリシャ語で岩や石を意味する「リトス」に替えたもの。本来はエアバッグなどを使って着地の衝撃を吸収しながら速度を下げる方法で、[[w:ja:マーズ・パスファインダー|マーズ・パスファインダー]]の着陸法にも採用されたが、KSPにそんなものは実装されていない。誤って墜落してしまったことを茶化したいときに使われる。 |
| + | |||
| + | ;Atmospheric entry / 大気圏突入 | ||
{{Main article|Atmospheric entry}} | {{Main article|Atmospheric entry}} | ||
| − | :大気圏に突入し、空気抵抗などを使って減速することによって、地表に向かって降下する弾道軌道をとること。現実の世界では、大気から再び宇宙空間に戻ってしまわないようなスピードまで十分減速させることは、機体に激しい熱を発生させる。 | + | :大気圏に突入し、空気抵抗などを使って減速することによって、地表に向かって降下する弾道軌道をとること。現実の世界では、大気から再び宇宙空間に戻ってしまわないようなスピードまで十分減速させることは、機体に激しい熱を発生させる。 |
| − | ;Burn / | + | :;Re-entry / 再突入 |
| + | ::大気圏突入と同じ意味だが、Kerbinの大気に突入する場合のみ、帰ってくるという意味で再突入という。 | ||
| + | |||
| + | ;<span id="burn">Burn / 燃焼(噴射)</span> | ||
:エンジンを燃焼させること。通常、何らかのかたちで軌道を変えるために行われる。 | :エンジンを燃焼させること。通常、何らかのかたちで軌道を変えるために行われる。 | ||
| − | ;Circularizing /真円化 | + | :;Retroburn / 逆噴射 |
| − | :周回軌道の[[#ecc|離心率]] | + | ::「後ろ向き」に行われる燃焼。例えば、エンジンがprogradeを向いていて、ノーズがretrogradeを向いているときに燃焼すること。[[#periapsis|periapsis]]や[[#apoapsis|apoapsis]]を下げるのに使われる一般的なマニューバである。 |
| − | ;Gravity turn/ 重力ターン | + | :;Radial burn/ラジアル噴射 |
| + | {{See also|Maneuver node|Maneuver node}} | ||
| + | ::*'''Radial-in burn/ラジアル・イン噴射''':Radial-in方向に行われる噴射。periapsisが天体の重心を通過するまで軌道を反時計回りに回転させる。 | ||
| + | ::*'''Radial-out burn/ラジアル・アウト噴射''':Radial-out方向に行われる噴射。periapsisが天体の重心を通過するまで軌道を時計回りに回転させる。 | ||
| + | |||
| + | ;<span id="Circularizing">Circularizing / 真円化</span> | ||
| + | :周回軌道の[[#ecc|離心率]]を0かそれに近づけること。つまり楕円をきれいな真円に近づけること。普通、apsisで燃焼することで行う。 | ||
| + | |||
| + | ;Gravity assist / 重力アシスト(スイングバイ) | ||
| + | {{see also||{{Wikipedia|lang=ja|スイングバイ}}}} | ||
| + | {{Main article|Tutorial:_Gravity_Assist/ja|重力アシスト}} | ||
| + | :天体の重力や公転運動エネルギーを利用して、燃料を消費せずに機体の速度や軌道を変えるマニューバ。効果はエンジンによる推進に比べれば小さいが燃料は節約できる。行ったあとに速度が上がるものを加速スイングバイ、速度が下がるものを減速スイングバイという。スイングバイ中にperiapsisで[[#burn|燃焼]]を行うものをパワードスイングバイといい、効率のよい加速・減速ができるが狙った軌道に投入するのは非常に難しい。 | ||
| + | |||
| + | ;<span id="Circularizing">Gravity turn / 重力ターン | ||
{{Main article|Gravity_turn/ja|重力ターン}} | {{Main article|Gravity_turn/ja|重力ターン}} | ||
| − | ;Maneuver node /マニューバ・ノード | + | :旋回しながら離陸していく、効率的な周回軌道投入法。 |
| + | |||
| + | ;Maneuver node / マニューバ・ノード | ||
{{Main article|Maneuver node}} | {{Main article|Maneuver node}} | ||
:マップ・ビューにおいて予定したマニューバ。 [[#burn|燃焼]]の効果を前もって教えてくれる。 | :マップ・ビューにおいて予定したマニューバ。 [[#burn|燃焼]]の効果を前もって教えてくれる。 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | == 物理 == |
| − | ;Acceleration | + | ;Velocity / 速度 |
| − | : | + | :位置の変化率である。速さと方向を合わせたものである。速度はベクトルであり、メートル/秒 (m/s) で測る。 |
| − | + | ||
| − | + | ;Acceleration / 加速度 | |
| − | ;Delta-v (Δv) | + | :速度の変化率。加速度は「m/s<sup>2</sup>」で測られるベクトルである。 |
| − | : | + | |
| − | ;Energy | + | ;Delta-v / デルタV (Δv) |
| + | :機体の推力によってなされた速度の変化分、あるいは速度を変化させる能力。メートル毎秒(m/s)によって測られる。Delta-vは、機体の重量が多いと低下し、比推力が高いと増加する。打ち上げロケットの効率性を計算するのに有用である。例えば、打ち上げロケットはKerbinの大気から抜け出し安定な周回軌道に入るために約3,400 m/sのdelta-vを必要とする。 | ||
| + | |||
| + | ;Energy / エネルギー | ||
{{See also||{{Wikipedia|Specific orbital energy}}}} | {{See also||{{Wikipedia|Specific orbital energy}}}} | ||
| − | : | + | :周回軌道にある物体のエネルギーは、位置エネルギーと運動エネルギーの合計である。 |
| − | : | + | :位置エネルギーは <math>E_p = -\frac{G M m}{R}</math> |
| − | : | + | :運動エネルギーは <math>E_k = \frac{1}{2} m v^2</math> |
| − | ;Escape Velocity | + | :(Gは[[w:Gravitational constant|重力定数]]、Mは[[celestial body|天体]]の質量、Rは天体の中心からの距離、vは速度) |
| − | : | + | :よって <math>E = E_k + E_p = \frac{1}{2} m v^2 - \frac{G M m}{R}</math> となる。 |
| − | ;g-force (G) | + | :この和は、推力を出していない限り一定である。つまり、periapsisに近づくにつれ位置エネルギーが運動エネルギーに変わり、periapsisを通過して離れていくにつれ再び運動エネルギーが位置エネルギーに変わる。エネルギーもしくは軌道エネルギーがゼロより大きいとき、機体は脱出軌道にある。 |
| − | : | + | :これがケプラーの法則の基本的な考え方であり、KSPのパッチドコニック法の元になっている。楕円は2つの焦点(foci)からの距離の和が一定となる点の集合である。焦点の一方は、周回される天体の重心である。そこに物体が近づくにつれ、位置エネルギーが運動エネルギーに変わる。同様に物体が焦点から遠ざかるにつれ、軌道が楕円なら、物体はもう一方の焦点に近づき、運動エネルギーが位置エネルギーに変換される。機体が天体へ真っ直ぐに向かっていく、あるいは離れていく場合、fociはapsisと一致し、apapsisで運動エネルギー0、periapsisで位置エネルギー0となる。軌道が完全な円である場合(Kerbinを回るMunの軌道など)、2つのfociは同一点となり、apsisの位置は定義されない(軌道上のすべての点がapsisとなる)。 |
| − | ;Gravity | + | :また、機体の質量を必要としない軌道エネルギー(<math>\epsilon</math>) もある: |
| − | : | + | :<math>E_p = \epsilon_p m</math> <math>E_k = \epsilon_k m</math> |
| − | + | :<math>E = \epsilon \, m = (\epsilon_k + \epsilon_p) m = -\frac{G M}{2 a}</math> | |
| − | : | + | :ここから同じ軌道長半径(''a'')をもつ軌道はすべて、同じ軌道エネルギーを持つことがわかる。 |
| − | + | ||
| − | {{Main article| | + | ;Escape Velocity / 脱出速度 |
| − | : | + | :惑星の重力圏から脱出するのに必要な速度のことで、<math>v_e = \sqrt{\frac{2GM}{r}}</math>で与えられる。Gは[[w:ja:万有引力定数|万有引力定数]]、Mは惑星の質量、rは惑星の半径。 |
| − | ;<span id="isp">Specific Impulse (I<sub>sp</sub>)</span> | + | |
| + | ;Tangential velocity / 接線速度 | ||
| + | :軌道の接線方向の速度成分。瞬間速度(計測時間をゼロに近づけたときの速度)は必ず軌道に対し接線方向である。 | ||
| + | |||
| + | ;Gravity / 重力(引力) | ||
| + | :質量を持つあらゆる物体が出している引き寄せる力。非常に弱い。普通、非常に質量の大きい物体(惑星や衛星など)のものしか感じられない。物体の重心からの距離の2乗に反比例する。つまり、物体との距離が2倍になれば、1/2<sup>2</sup> = 1/4の重力しか感じない。 | ||
| + | |||
| + | ;g-force / Gフォース (G) | ||
| + | :地球の海面高度での重力加速度(9.81 m/s²)を1 Gとしたときの、加速度を表す単位。つまり、地球の表面にある物体には1 Gで加速している。加速度が2 Gのとき物体の重さは2倍になり、0 Gのとき重さは無くなる。周回軌道のように自由落下しているとき、つまりエンジンを燃焼しておらず空気抵抗もないとき、加速を感じなくなり0 Gと表現される。 | ||
| + | |||
| + | ;Gravity Well / 重力圏 | ||
| + | :惑星の重力の影響を受ける範囲のこと。現実には無限に広がっているが、距離の2乗に反比例して減少する(距離が2倍になれば重力は4分の1になる)ので、惑星の周囲の影響圏でのみ重要である。KSPでは「パッチドコニック法」を使用しているので影響圏以外での重力はまったくシミュレートされていない。 | ||
| + | :;<span id="soi">Sphere of influence</span> / 影響圏(作用圏) | ||
| + | :{{Main article|Sphere of influence}} | ||
| + | ::天体から無視できない重力の影響を受ける範囲。SoI/SOIと略す。重力圏とほぼ同じ意味。 | ||
| + | |||
| + | ;<span id="isp">Specific Impulse / 比推力 (I<sub>sp</sub>)</span> | ||
{{Main article|Specific impulse}} | {{Main article|Specific impulse}} | ||
| − | :<math | + | :<math>I_{sp}= \frac{T}{\dot m}</math> 、 <math>[I_{sp}] = \frac{m}{s}</math> |
| − | : | + | :I<sub>sp</sub>は推進システムがどれほど効率的かを定義する。I<sub>sp</sub>が高ければ、同じ燃料量でより強力な推力が出される。 |
| − | + | :I<sub>sp</sub>は普通「秒」で与えられるが、実際は物理的に正しい単位は「距離/時間」であり、普通「メートル/秒」もしくは「フィート/秒」で与えられる。速度の単位との混同を避けるため、物理的に正しいI<sub>sp</sub>(「距離/時間」)を地球の表面重力(9.81 m/s²)で割る。その結果、値は「秒」で表される。I<sub>sp</sub>を公式で使う場合は「距離/時間」に直す必要があり、そのためには地球の表面重力を再び掛けなければならない。この値は、これら2つの単位を変換するためだけに使われているので、'''重力が変化しても比推力は変化しない'''。KSPでは9.82 m/s²の値が使われているようなので、やや少ない燃料しか消費しない。 | |
| − | + | :比推力は推力と燃料流量の比率なので <math>\frac{Ns}{kg}</math> が単位として使われることもある。 | |
| − | : | + | :これは <math>\frac{m}{s} = kg \cdot \frac{m}{s^2} \cdot \frac{s}{kg}</math> を数学的に変形したものである。 |
| − | + | :なぜなら力の定義は質量掛ける加速度だからだ: <math>N = kg \cdot \frac{m}{s^2}</math> | |
| − | + | :よって <math>1 \frac{Ns}{kg} = 1 \frac{m}{s}</math> となる。 | |
| − | ;<span id="TWR">Thrust-to-weight ratio</span> | + | :後者の方は単純にSI単位のみを使っている。 |
| + | |||
| + | ;<span id="TWR">Thrust-to-weight ratio</span> / 推力重量比(TWR) | ||
{{See also|Thrust-to-weight ratio}} | {{See also|Thrust-to-weight ratio}} | ||
| − | :<math | + | :<math>\text{TWR} = \frac{T}{W} = \frac{T}{m \cdot g}</math> |
| − | + | :機体の、あるステージでの総重量と、そこで使用可能な全ての推進機器の推力の比率である。TWRが1より大きければ、垂直方向に加速して上昇するのに充分な推力があることを意味する。TWRが1より小さければ、低い高度では重力と空気抵抗に勝てないが、宇宙空間ではマニューバに時間が掛かることだけを意味する。なぜなら重量(W)はその時の重力加速度(g)によって変わり、TWRはその時どの天体から影響を受けているかによって変わるからだ。[[Mun/ja|Mun]]地表ではKerbinの重力加速度の16.6%しかなく、TWR<sub>Kerbin</sub> = 1のときTWR<sub>Mun</sub> = 6となる。 | |
| − | |||
| − | |||
| − | |||
| − | == | + | ==関連項目== |
| − | * [[Tutorials]] | + | * [[Tutorials/ja|チュートリアル]] |
| − | * [[Acronyms and Initialisms]] | + | * [[Acronyms and Initialisms/ja|略語集]] |
| − | * [[Deep Space Kraken]] | + | * [[Deep Space Kraken/ja|深宇宙クラーケン]] |
[[Category:Terminology/ja]] | [[Category:Terminology/ja]] | ||
Latest revision as of 05:24, 21 July 2019
KSPには軌道や物理に関するたくさんの用語が登場するので素人には少々取っつきにくいところがあります。 また、一般的な用語の代わりに様々な科学用語や略語が使われていたりもします。
このページでは、重要な用語をリストアップし、簡潔に説明していきます。これであなたも一人前の宇宙飛行士!?
Contents
数学
- Elliptical/楕円
- 周回軌道はふつう楕円軌道である。
- Hyperbolic/双曲線
- 開いた滑らかな曲線。離脱軌道などは双曲線になる。
- Normal vector/法線ベクトル
- 基準面に対して垂直なベクトル。
- Scalar/スカラー
- 方向を持たないただの値。普通そのスカラーの次元が何なのかを示す単位が伴う。例えば3 m/sや、3 mや、3 sは、それぞれ速さ、距離、時間の単位が付いているが、方向がないのでスカラーである。
- Vector/ベクトル
- 方向と値がセットになったもの。例えば、方位(方向)と速さが一緒になった「速度(velocity)」はベクトル。座標系が何であるか、何次元を考えるかによって、ベクトルの表され方は異なる。 <35°, 12>は2次元の極座標ベクトル、<14, 9, -20>は3次元の直交座標ベクトルである。他にも座標系はあるが、この2つが一番よくつかわれる。
- <35°, 12> は、原点から35°(基準軸Xから反時計回りに大きくなる)の角度に向かって伸びる、長さ12の矢印である。(長さが0の場合、角度はない)
- <14, 9, -20> は、原点(<0,0,0>)から、X座標=14、Y座標=9、Z座標=-20の点に向かって伸びる矢印である。
- 直交座標を使う利点は、到着点がはっきり分かる点である。欠点は長さが分かりずらいことである。逆に、極座標は簡単に長さがわかるが、到着点がわかりずらい。
- velocity(速度), acceleration(加速度), force(力)はすべてベクトルである。
3次元座標系では
- 基準点。つまり出発点。
- 3つの基底ベクトル。軸の基本単位と、その方向を定義する。
- その座標系での位置を表す、角度か座標の3つのスカラー。
が必要である。
軌道の種類
- Trajectory / 軌道
- 軌道とは時間に従って物体が宇宙を進んでいく経路である。
- Ballistic trajectory / 弾道
- 落ちている物体の軌道は弾道である。ロケット工学では、重力以外なんの力(推力等)も働いていない物体の軌道をいう。
- Orbit / 周回軌道
- → メイン記事: Orbit
- 充分な接線速度を持つ(かつ大気圏外にあり空気抵抗を受けない)と、物体は常に惑星の「隣り」に落ちることを繰り返す(地面に落ちない)。このような軌道を周回軌道という。安定した周回軌道は楕円(円は離心率ゼロの楕円)である。接線速度が脱出速度を超えると周回軌道は放物線もしくは双曲線になる。
- Sub-orbital / 準軌道
- periapsisが天体の表面よりも低い軌道のこと。つまり、いったん宇宙に飛び出すが、再び地表に戻ってくるような軌道。
軌道の要素
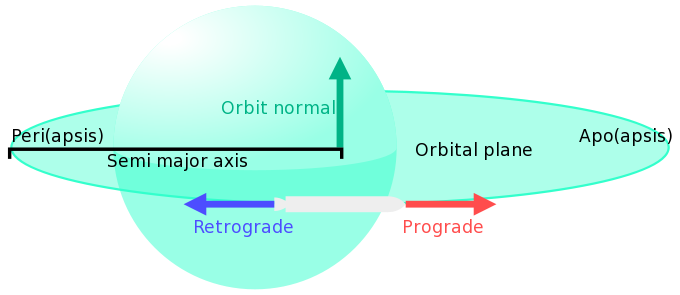
- Apsis / 極点
- → 参照: “Apoapsis and periapsis” section in Orbit
- 楕円軌道には次の2つのapsisが必ず存在する。
- Apoapsis/遠点:天体から最も遠い点(軌道の最高点)。マップではAPと表示される。アポジともいう。
- Periapsis/近点:天体から最も近い点(軌道の最低点)。マップではPEと表示される。ペリジともいう。
- Apsisは楕円の長軸上に存在し、互いに天体を挟んで反対に位置する。
- 天体との距離を計算する公式は中心点からの距離を使うが、apsisは表面からの距離なので、それに天体の半径分を加算する必要がある。
- Peri~とApo~:特定の天体のApsisであることを強調したいとき、後ろに天体名をもじってつける。例えばKerbinの周回軌道の場合は~keeや~kerbをつけて、Perikee/Perikerbと言ったりApokee/Apokerbと言ったりする。
- Orbital plane / 軌道面
- 天体を回る軌道が描く仮想の円盤。
- Reference plane / 基準面
- 現在の軌道を記述するために基準とするあらゆる平面のこと。惑星を周回する軌道の場合、赤道面が基準面になる。太陽系において複数の天体がからむ場合、黄道面が基準面になる。他の物体をインターセプトする場合、その物体の軌道が基準面になる。基準面に対するinclinationとascending nodeの経度を知ることで、軌道面を完全に記述することができる。
- Inclination / 傾斜角
- → 参照: “Inclination” section in Orbit
- 軌道面と基準面の間の角度(例:赤道面に対しinclinationが90°の軌道は極軌道となる)
- Orbital node / 交点
- 基準面と軌道面が交差する点。実際の天文学的定義とは異なるがゲーム内ではApsisもこれに含まれる。
- Ascending node/昇交点:軌道が北向きに交差する点。マップではANと表示される。
- Descending node/降交点:軌道が南向きに交差する点。マップではDNと表示される。
- Eccentricity / 離心率
- → 参照: “Eccentricity” section in Orbit
- 軌道がどれだけ真円からかけ離れているかを表すスカラーである。
-
- ecc = 0 → 真円軌道
- 0 < ecc < 1 → 楕円軌道
- ecc = 1 → 放物線軌道(離脱軌道はこれ)
- ecc > 1 → 双曲線軌道(離脱軌道はこれ)
- Semi-major axis / 軌道長半径
- → 参照: “Semi-major axis” section in Orbit
- 楕円の長軸をmajor-axisといい、sami-major axis(a)はその半径である。apoapsis (Ap) とperiapsis (Pe)の平均から求まる。もちろん、これに天体の半径(R)を加算しなければならない。軌道長半径が同じ軌道は、離心率によらず、必ず同じ周期になる。
- Sidereal period / 恒星周期
- 恒星周期は、物体が恒星の周りを一周するのにかかる時間である。これは慣性系(非回転座標系)における公転周期である。
- Synodic period / 会合周期
- 会合周期とは、2つ以上の物体の関係において、ある物体が再び同じ位置に戻るまでにかかる時間。例えば、Kerbolから観測したとき、Kerbinに対してMunが再び同じ満ち欠けに見える位置に来るまでの時間。Kerbol-Kerbinラインを考えたとき、再びそのラインに交わるまでの時間と同じ。公転周期の一つだが、Kerbolを周回するKerbinから観測しているため、恒星周期とは異なる。
- Low orbit / 低軌道
- 大気の空気抵抗などの影響を受けず、安定した軌道を保つのに必要最低限な高度の周回軌道のこと。低軌道は地表から最小の燃料で到達でき、離脱燃焼がどの方向にもできるので、上昇したあと次のランデブー目標(惑星や宇宙船)へ向かうまでの、踏み石として使われる。Kerbinの低軌道はおよそ80km~100kmである。大気のない天体では、理論上、地面より高ければどこでも軌道がとれるが、10km以下だと山や高地に激突する危険性が非常に高い。低軌道でのタイムワープは低く抑えられている。
方向
軌道における方向
- Radial-in/ラジアル・イン
- 天体の中心に向かう方向。radial-outの反対。
- Radial-out/ラジアル・アウト
- 天体の中心から離れる方向。radial-inの反対。
- Orbit normal/オービット・ノーマル
- 軌道面の法線ベクトル。船の速度と重力の外積にあたる。右手の法則において中指を重力方向、人差し指を速度方向としたときの親指の方向がOrbital Normal。船が反時計回りに回っているときは、「Up」となり、時計回りに回っているときは「Down」となる。「Up」の代わりに「North」や「N+」と書くことがある。同様に「Down」を「Anti-Normal」「South」「N-」と書くことがある。
- Prograde/順行
- 船が軌道に沿って進んでいる方向。軌道はふつう楕円なので、常に、船がいる点における接線となる。
- Retrograde/逆行
- Progradeの反対方向。軌道に沿って後ろ向き。
船における方向
- Zenith /天頂
- 船の天井側。普通、天体から離れていく方向。Radial-outと同じ。Nadirの反対。
- Nadir /天底
- 船の床側。普通、天体に向かっていく方向。Radial-inと同じ。Zenithの反対。
- Port(side) /左舷
- 船の左側。starboardの反対。
- Starboard /右舷
- 船の右側。port(side)の反対側。
- Front /前
- 船の前方。通常、ノーズやprogradeと同じ。aftの反対。
- Aft /後
- 船の後方。通常、船のエンジンがついている方向、retrogradeと同じ。frontの反対。
マニューバ
- Atmospheric braking / エアロブレーキ
- → メイン記事: エアロブレーキング
- periapsisを惑星の大気を通るように下げること。こうすることによって空気抵抗が船のスピードを低下させる。そのまま大気圏突入に繋げることもできるし、燃料を使わずに軌道を大きく変えることができる。空力ブレーキ、大気ブレーキともいう。
- Lithobraking / リトブレーキ
- → 参照: Lithobraking on Wikipedia
- 空気の代わりに地面を使ってブレーキを行うこと。エアロブレーキの「エアロ」をギリシャ語で岩や石を意味する「リトス」に替えたもの。本来はエアバッグなどを使って着地の衝撃を吸収しながら速度を下げる方法で、マーズ・パスファインダーの着陸法にも採用されたが、KSPにそんなものは実装されていない。誤って墜落してしまったことを茶化したいときに使われる。
- Atmospheric entry / 大気圏突入
- → メイン記事: Atmospheric entry
- 大気圏に突入し、空気抵抗などを使って減速することによって、地表に向かって降下する弾道軌道をとること。現実の世界では、大気から再び宇宙空間に戻ってしまわないようなスピードまで十分減速させることは、機体に激しい熱を発生させる。
- Re-entry / 再突入
- 大気圏突入と同じ意味だが、Kerbinの大気に突入する場合のみ、帰ってくるという意味で再突入という。
- Burn / 燃焼(噴射)
- エンジンを燃焼させること。通常、何らかのかたちで軌道を変えるために行われる。
- → 参照: Maneuver node
- Radial-in burn/ラジアル・イン噴射:Radial-in方向に行われる噴射。periapsisが天体の重心を通過するまで軌道を反時計回りに回転させる。
- Radial-out burn/ラジアル・アウト噴射:Radial-out方向に行われる噴射。periapsisが天体の重心を通過するまで軌道を時計回りに回転させる。
- Circularizing / 真円化
- 周回軌道の離心率を0かそれに近づけること。つまり楕円をきれいな真円に近づけること。普通、apsisで燃焼することで行う。
- Gravity assist / 重力アシスト(スイングバイ)
- → 参照: スイングバイ on Wikipedia
- → メイン記事: 重力アシスト
- 天体の重力や公転運動エネルギーを利用して、燃料を消費せずに機体の速度や軌道を変えるマニューバ。効果はエンジンによる推進に比べれば小さいが燃料は節約できる。行ったあとに速度が上がるものを加速スイングバイ、速度が下がるものを減速スイングバイという。スイングバイ中にperiapsisで燃焼を行うものをパワードスイングバイといい、効率のよい加速・減速ができるが狙った軌道に投入するのは非常に難しい。
- Gravity turn / 重力ターン
- → メイン記事: 重力ターン
- 旋回しながら離陸していく、効率的な周回軌道投入法。
- Maneuver node / マニューバ・ノード
- → メイン記事: Maneuver node
- マップ・ビューにおいて予定したマニューバ。 燃焼の効果を前もって教えてくれる。
物理
- Velocity / 速度
- 位置の変化率である。速さと方向を合わせたものである。速度はベクトルであり、メートル/秒 (m/s) で測る。
- Acceleration / 加速度
- 速度の変化率。加速度は「m/s2」で測られるベクトルである。
- Delta-v / デルタV (Δv)
- 機体の推力によってなされた速度の変化分、あるいは速度を変化させる能力。メートル毎秒(m/s)によって測られる。Delta-vは、機体の重量が多いと低下し、比推力が高いと増加する。打ち上げロケットの効率性を計算するのに有用である。例えば、打ち上げロケットはKerbinの大気から抜け出し安定な周回軌道に入るために約3,400 m/sのdelta-vを必要とする。
- Energy / エネルギー
- → 参照: Specific orbital energy on Wikipedia
- 周回軌道にある物体のエネルギーは、位置エネルギーと運動エネルギーの合計である。
- 位置エネルギーは
- 運動エネルギーは
- (Gは重力定数、Mは天体の質量、Rは天体の中心からの距離、vは速度)
- よって となる。
- この和は、推力を出していない限り一定である。つまり、periapsisに近づくにつれ位置エネルギーが運動エネルギーに変わり、periapsisを通過して離れていくにつれ再び運動エネルギーが位置エネルギーに変わる。エネルギーもしくは軌道エネルギーがゼロより大きいとき、機体は脱出軌道にある。
- これがケプラーの法則の基本的な考え方であり、KSPのパッチドコニック法の元になっている。楕円は2つの焦点(foci)からの距離の和が一定となる点の集合である。焦点の一方は、周回される天体の重心である。そこに物体が近づくにつれ、位置エネルギーが運動エネルギーに変わる。同様に物体が焦点から遠ざかるにつれ、軌道が楕円なら、物体はもう一方の焦点に近づき、運動エネルギーが位置エネルギーに変換される。機体が天体へ真っ直ぐに向かっていく、あるいは離れていく場合、fociはapsisと一致し、apapsisで運動エネルギー0、periapsisで位置エネルギー0となる。軌道が完全な円である場合(Kerbinを回るMunの軌道など)、2つのfociは同一点となり、apsisの位置は定義されない(軌道上のすべての点がapsisとなる)。
- また、機体の質量を必要としない軌道エネルギー() もある:
- ここから同じ軌道長半径(a)をもつ軌道はすべて、同じ軌道エネルギーを持つことがわかる。
- Escape Velocity / 脱出速度
- 惑星の重力圏から脱出するのに必要な速度のことで、で与えられる。Gは万有引力定数、Mは惑星の質量、rは惑星の半径。
- Tangential velocity / 接線速度
- 軌道の接線方向の速度成分。瞬間速度(計測時間をゼロに近づけたときの速度)は必ず軌道に対し接線方向である。
- Gravity / 重力(引力)
- 質量を持つあらゆる物体が出している引き寄せる力。非常に弱い。普通、非常に質量の大きい物体(惑星や衛星など)のものしか感じられない。物体の重心からの距離の2乗に反比例する。つまり、物体との距離が2倍になれば、1/22 = 1/4の重力しか感じない。
- g-force / Gフォース (G)
- 地球の海面高度での重力加速度(9.81 m/s²)を1 Gとしたときの、加速度を表す単位。つまり、地球の表面にある物体には1 Gで加速している。加速度が2 Gのとき物体の重さは2倍になり、0 Gのとき重さは無くなる。周回軌道のように自由落下しているとき、つまりエンジンを燃焼しておらず空気抵抗もないとき、加速を感じなくなり0 Gと表現される。
- Gravity Well / 重力圏
- 惑星の重力の影響を受ける範囲のこと。現実には無限に広がっているが、距離の2乗に反比例して減少する(距離が2倍になれば重力は4分の1になる)ので、惑星の周囲の影響圏でのみ重要である。KSPでは「パッチドコニック法」を使用しているので影響圏以外での重力はまったくシミュレートされていない。
- Sphere of influence / 影響圏(作用圏)
- → メイン記事: Sphere of influence
- 天体から無視できない重力の影響を受ける範囲。SoI/SOIと略す。重力圏とほぼ同じ意味。
- Specific Impulse / 比推力 (Isp)
- → メイン記事: Specific impulse
- 、
- Ispは推進システムがどれほど効率的かを定義する。Ispが高ければ、同じ燃料量でより強力な推力が出される。
- Ispは普通「秒」で与えられるが、実際は物理的に正しい単位は「距離/時間」であり、普通「メートル/秒」もしくは「フィート/秒」で与えられる。速度の単位との混同を避けるため、物理的に正しいIsp(「距離/時間」)を地球の表面重力(9.81 m/s²)で割る。その結果、値は「秒」で表される。Ispを公式で使う場合は「距離/時間」に直す必要があり、そのためには地球の表面重力を再び掛けなければならない。この値は、これら2つの単位を変換するためだけに使われているので、重力が変化しても比推力は変化しない。KSPでは9.82 m/s²の値が使われているようなので、やや少ない燃料しか消費しない。
- 比推力は推力と燃料流量の比率なので が単位として使われることもある。
- これは を数学的に変形したものである。
- なぜなら力の定義は質量掛ける加速度だからだ:
- よって となる。
- 後者の方は単純にSI単位のみを使っている。
- Thrust-to-weight ratio / 推力重量比(TWR)
- → 参照: Thrust-to-weight ratio
- 機体の、あるステージでの総重量と、そこで使用可能な全ての推進機器の推力の比率である。TWRが1より大きければ、垂直方向に加速して上昇するのに充分な推力があることを意味する。TWRが1より小さければ、低い高度では重力と空気抵抗に勝てないが、宇宙空間ではマニューバに時間が掛かることだけを意味する。なぜなら重量(W)はその時の重力加速度(g)によって変わり、TWRはその時どの天体から影響を受けているかによって変わるからだ。Mun地表ではKerbinの重力加速度の16.6%しかなく、TWRKerbin = 1のときTWRMun = 6となる。
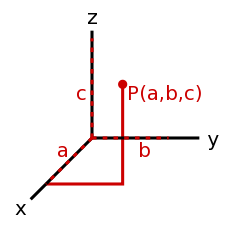
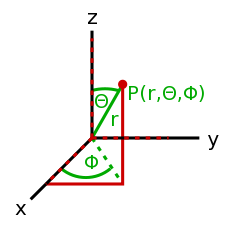











![{\displaystyle [I_{sp}]={\frac {m}{s}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/072515563895cdf8f2d19f1dab433618230ce14f)




