Difference between revisions of "Atmosphere/pt"
m (Blanked the page) |
m (Reverted edits by Rocketing Rudolph (talk) to last revision by Brendocosta) |
||
| Line 1: | Line 1: | ||
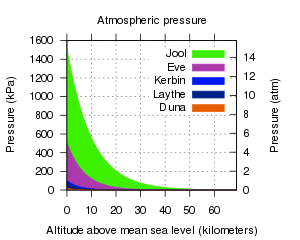
| + | [[File:Pressures.svg|thumb|As pressões para todas as atmosferas]] | ||
| + | {| class="wikitable float-right" | ||
| + | ! colspan="4" | Planetas | ||
| + | ! style="border-left-width:2px;" colspan="2" | Luas | ||
| + | |- | ||
| + | | style="border-right:0px;" | [[File:TinyEve.png|16px]] | ||
| + | | style="border-left:0px;" | [[Eve/pt|Eve]] | ||
| + | | style="border-right:0px;" | [[File:TinyKerbin.png|16px]] | ||
| + | | style="border-left:0px;" | [[Kerbin/pt|Kerbin]] | ||
| + | | style="border-left-width:2px; border-right:0px; vertical-align:top;" rowspan="2" | [[File:TinyLaythe.png|16px]] | ||
| + | | style="border-left:0px; vertical-align:top;" rowspan="2" | [[Laythe/pt|Laythe]] | ||
| + | |- | ||
| + | | style="border-right:0px;" | [[File:TinyDuna.png|16px]] | ||
| + | | style="border-left:0px;" | [[Duna/pt|Duna]] | ||
| + | | style="border-right:0px;" | [[File:TinyJool.png|16px]] | ||
| + | | style="border-left:0px;" | [[Jool/pt|Jool]] | ||
| + | |} | ||
| + | A '''atmosfera''' de um corpo celeste retarda o movimento de qualquer objeto que passa por ele, uma força conhecida como arrasto atmosférico (ou simplesmente '''drag''', em inglês). Uma atmosfera também permite a elevação aerodinâmica. Os corpos celestes com atmosferas são os planetas [[Eve/pt|Eve]], [[Kerbin/pt|Kerbin]], [[Duna/pt|Duna]] e [[Jool/pt|Jool]], bem como [[Laythe/pt|Laythe]], uma das luas de Jool. Apenas Kerbin e Laythe têm atmosferas que contêm oxigênio e, portanto, produzem [[Intake air/pt|ar de admissão]] para [[Jet engine/pt|motores à jato]] funcionarem. | ||
| + | |||
| + | Atmosferas permitem [[Aerobraking/pt|aerofrenagem]], que utiliza a própria atmosfera é mais fácil para pouso. No entanto, uma atmosfera faz decolar de um planeta mais difícil e aumenta a altitude mínima de uma órbita estável. | ||
| + | |||
| + | == Arrasto == | ||
| + | [[File:Mk16-XL Parachute.jpg|thumb|right|Um Command Pod Mk1-2 com um pára-quedas MK16-XL sendo retardado por arrasto na atmosfera de Kerbin.]] | ||
| + | |||
| + | No jogo, a força de arrasto atmosférico (''F<sub>D</sub>'') é modelado como se segue:<ref>http://forum.kerbalspaceprogram.com/showthread.php/5235-Atmospheric-drag?p=88804&viewfull=1#post88804</ref> | ||
| + | |||
| + | : <math>F_D = 0.5\, \rho\, v^2\, d\, A</math> | ||
| + | |||
| + | onde ''ρ'' é a densidade atmosférica (kg/m<sup>3</sup>), ''V'' é a velocidade do navio (m/s), ''d'' é o coeficiente de arrasto (adimensional), e ''A'' é a [[w:cross section (geometry)|cross-sectional area]] (m<sup>2</sup>). | ||
| + | |||
| + | Note-se que a área de secção transversal não é realmente calculado no jogo. Em vez disso é Supõe-se que é directamente proporcional à massa, que é uma simplificação irrealista feita por KSP. o parâmetro [[API:FlightGlobals|FlightGlobals]].Múltiplo arrastro indica que a relação de proporcionalidade é 0.008 m<sup>2</sup>/kg, assim: | ||
| + | |||
| + | : <math>A = 0.008 \cdot m</math> | ||
| + | |||
| + | onde ''M'' é a massa do navio (kg). | ||
| + | |||
| + | A densidade atmosférica ''ρ'' é diretamente proporcional à pressão atmosférica (''p'' da unidade ''atm''), que é uma função da altitude, a pressão da atmosfera em altitude 0 (''p<sub>0</sub>''), e altura escala (''H''): | ||
| + | |||
| + | : <math>\begin{align} | ||
| + | p &= p_0 \cdot e^\frac{-altitude}{H} \\ | ||
| + | \rho &= 1.2230948554874 \frac{\text{kg}}{\text{m}^3 \cdot \text{atm}} \cdot p | ||
| + | \end{align}</math> | ||
| + | |||
| + | em que p é aqui em unidades atm, e ''ρ'' em kg/m<sup>3</sup>. O fator de conversão de 1.2230948554874 kg/(m<sup>3</sup>·atm) é dado pela [[API:FlightGlobals|FlightGlobals]].getAtmDensity(1.0), que retorna a densidade a 1 atmosfera (do nível do mar em Kerbin) de pressão. | ||
| + | |||
| + | O coeficiente de arrasto ('' d '') é calculada como a média ponderada de massa dos valores max_drag de todas as partes na nave. Para a maioria das naves sem pára-quedas implantados, ''d'' será muito próximo de 0,2, uma vez que este é o valor max_drag da grande maioria das peças. Além disso, um grupo da mesma parte tem sempre o mesmo coeficiente de arrasto. | ||
| + | |||
| + | Como um exemplo, o coeficiente de arrasto para uma embarcação que consiste simplesmente de um [[Mk1-2 comando Pod]] (massa 4, arraste 0,2) e um implantado Mk16-XL Parachute (massa 0.3 arraste 500) é: | ||
| + | |||
| + | : <math>\frac{4 \cdot 0.2 + 0.3 \cdot 500}{4 + 0.3} = 35.07</math> | ||
| + | |||
| + | == A velocidade terminal == | ||
| + | A velocidade terminal de um objeto que cai através de uma atmosfera, é a velocidade a que a força da gravidade é igual à força de arrasto. Mudanças velocidade terminal em função da altitude. Com tempo suficiente, um objeto caindo na atmosfera vai desacelerar a velocidade terminal e, em seguida, permanecer em velocidade terminal para o resto de sua queda. | ||
| + | |||
| + | Velocidade terminal é importante porque é ela que descreve a quantidade de velocidade que uma nave espacial deve queimar quando estiver perto do chão, e também representa a velocidade com que uma nave deve estar viajando para cima durante uma subida de combustível ideal. | ||
| + | |||
| + | |||
| + | A força da gravidade (''F<sub>G</sub>'') é: | ||
| + | |||
| + | : <math>F_G = m \cdot a = m \cdot \frac{GM}{r^2}</math> | ||
| + | |||
| + | onde ''M'' ainda é a massa do navio, ''G'' é o constante gravitacional, ''M'' é a massa do planeta, e ''R'' é o distância do ''centro'' do planeta para o objeto em queda. | ||
| + | |||
| + | Para encontrar a velocidade terminal, montamos ''F<sub>G</sub>'' equal to ''F<sub>D</sub>'': | ||
| + | |||
| + | : <math>\begin{align} | ||
| + | m \cdot \frac{GM}{r^2} &= 0.5 \cdot \rho \cdot v^2 \cdot d \cdot \left(0.008 \frac{\text{m}^2}{\text{kg}} \cdot m\right) \\ | ||
| + | \frac{GM}{r^2} &= 0.004\frac{\text{m}^2}{\text{kg}} \cdot \rho \cdot v^2 \cdot d \\ | ||
| + | v &= v_T = \sqrt{\frac{250 \frac{\text{kg}}{\text{m}^2} \cdot GM}{r^2 \cdot \rho \cdot d}} | ||
| + | \end{align}</math> | ||
| + | |||
| + | Partindo do princípio de '' d '' é de 0,2 (o que é uma boa aproximação, pára-quedas previstas não estão em uso), isso simplifica a: | ||
| + | |||
| + | : <math>v_T = \sqrt{\frac{1250 \frac{\text{kg}}{\text{m}^2} \cdot GM}{r^2\, \rho}}</math> | ||
| + | |||
| + | Para o pod Mk1-2 e exemplo de pára-quedas Mk16XL foto acima, o coeficiente de arrasto é 35,07, pelo que a sua velocidade terminal ao nível do mar em Kerbin (que é 600 & nbsp; km do centro de Kerbin) é: | ||
| + | |||
| + | |||
| + | : <math>v_T = \sqrt{\frac{250 \frac{\text{kg}}{\text{m}^2} \cdot GM}{r^2\, \rho \cdot 35.07}}</math> | ||
| + | |||
| + | : <math>\rho = 1.2230948554874 \frac{\text{kg}}{\text{m}^3 \cdot \text{atm}} \cdot 1 \text{atm} \cdot e^\frac{-0 \text{m}}{5000 \text{m}}</math> | ||
| + | |||
| + | : <math>v_T = \sqrt{\frac{250 \frac{\text{kg}}{\text{m}^2} \cdot 6.674 \cdot 10^{-11} \frac{\text{m}^3}{\text{kg} \cdot \text{s}^2} \cdot 5.2915793 \cdot 10^{22} \operatorname{kg}}{(600000 \operatorname{m})^2 \cdot 1.2230948554874 \frac{\text{kg}}{\text{m}^3} \cdot 35.07}} = 7.56 \frac{\text{m}}{\text{s}}</math> | ||
| + | |||
| + | === Exemplos === | ||
| + | {| class="wikitable" | ||
| + | !rowspan=2 valign=bottom| Altitude (m) ||colspan=6| v<sub>T</sub> (m/s) | ||
| + | |- | ||
| + | ! Eve !! Kerbin !! Duna !! Jool !! Laythe | ||
| + | |- | ||
| + | | 0 || {{sigfigs|{{VT | planet=Eve | alt= 0}}|5}} || {{sigfigs|{{VT | planet=Kerbin | alt= 0}}|5}} || {{sigfigs|{{VT | planet=Duna | alt= 0}}|5}} || {{sigfigs|{{VT | planet=Jool | alt= 0}}|5}} || {{sigfigs|{{VT | planet=Laythe | alt= 0}}|5}} | ||
| + | |- | ||
| + | | 100 || {{sigfigs|{{VT | planet=Eve | alt= 100}}|5}} || {{sigfigs|{{VT | planet=Kerbin | alt= 100}}|5}} || {{sigfigs|{{VT | planet=Duna | alt= 100}}|5}} || {{sigfigs|{{VT | planet=Jool | alt= 100}}|5}} || {{sigfigs|{{VT | planet=Laythe | alt= 100}}|5}} | ||
| + | |- | ||
| + | | 1000 || {{sigfigs|{{VT | planet=Eve | alt= 1000}}|5}} || {{sigfigs|{{VT | planet=Kerbin | alt= 1000}}|5}} || {{sigfigs|{{VT | planet=Duna | alt= 1000}}|5}} || {{sigfigs|{{VT | planet=Jool | alt= 1000}}|5}} || {{sigfigs|{{VT | planet=Laythe | alt= 1000}}|5}} | ||
| + | |- | ||
| + | | 10000 || {{sigfigs|{{VT | planet=Eve | alt=10000}}|5}} || {{sigfigs|{{VT | planet=Kerbin | alt=10000}}|5}} || {{sigfigs|{{VT | planet=Duna | alt=10000}}|5}} || {{sigfigs|{{VT | planet=Jool | alt=10000}}|5}} || {{sigfigs|{{VT | planet=Laythe | alt=10000}}|5}} | ||
| + | |} | ||
| + | |||
| + | == On-rails de física == | ||
| + | Se uma nave é "on rails" (ou seja, é mais do que 2.25 km a partir do navio-controlado ativamente) e sua órbita passa através da atmosfera de um planeta, uma das duas coisas vai acontecer com base na pressão atmosférica em altitude do navio: | ||
| + | |||
| + | * Abaixo de 0.01 atm: nenhum arrasto atmosférico ocorrerá e a nave será completamente afetada. | ||
| + | * 0.01 atm ou acima: a nave irá desaparecer. | ||
| + | |||
| + | A tabela a seguir mostra a altitude desta 0,01 atm para cada corpo celeste com uma atmosfera: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Body || Altitude (m) | ||
| + | |- | ||
| + | | [[Eve]] ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Eve}}}} | ||
| + | |- | ||
| + | | [[Kerbin]] ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Kerbin}}}} | ||
| + | |- | ||
| + | | [[Duna]] ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Duna}}}} | ||
| + | |- | ||
| + | | [[Jool]] ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Jool}}}} | ||
| + | |- | ||
| + | | [[Laythe]] ||align="right"| {{Formatnum|{{Body data/alt at pressure|pressure=0.01|body=Laythe}}}} | ||
| + | |} | ||
| + | |||
| + | == Altura atmosférica == | ||
| + | A altura atmosférica depende da altura escala do corpo celestial e é onde 0.000001<sup>th</sup> (0.0001%) de a superfície de pressão está permanecendo assim a pressão atmosférica na fronteira não é constante. Tecnicamente, uma nave em órbita de Jool pode ir mais baixo para a atmosfera (ou a atmosfera começa a partir de uma pressão mais elevada). | ||
| + | :<math>alt_{\text{atmospheric height}} = -ln\left(10^{-6}\right) \cdot \text{scale height}</math> | ||
| + | :<math>p_{\text{atmospheric height}} = p_0 \cdot 10^{-6}</math> | ||
| + | A atmosfera de Kerbin termina em 0.000001 & nbsp; atm e calcular onde os outros corpos celestes devem ter a altura atmosférica: | ||
| + | :<math>alt_{\text{atmospheric height (real)}} = -ln\left(\frac{10^{-6}}{p_0}\right) \cdot \text{scale height}</math> | ||
| + | |||
| + | == Veja também == | ||
| + | * [[Atmospheric entry/pt|Reentrada atmosférica]] | ||
| + | |||
| + | == Notes == | ||
| + | <references /> | ||
Revision as of 18:48, 17 March 2017
| Planetas | Luas | ||||
|---|---|---|---|---|---|
| |
Eve | |
Kerbin | |
Laythe |
| |
Duna | |
Jool | ||
A atmosfera de um corpo celeste retarda o movimento de qualquer objeto que passa por ele, uma força conhecida como arrasto atmosférico (ou simplesmente drag, em inglês). Uma atmosfera também permite a elevação aerodinâmica. Os corpos celestes com atmosferas são os planetas Eve, Kerbin, Duna e Jool, bem como Laythe, uma das luas de Jool. Apenas Kerbin e Laythe têm atmosferas que contêm oxigênio e, portanto, produzem ar de admissão para motores à jato funcionarem.
Atmosferas permitem aerofrenagem, que utiliza a própria atmosfera é mais fácil para pouso. No entanto, uma atmosfera faz decolar de um planeta mais difícil e aumenta a altitude mínima de uma órbita estável.
Contents
Arrasto
No jogo, a força de arrasto atmosférico (FD) é modelado como se segue:[1]
onde ρ é a densidade atmosférica (kg/m3), V é a velocidade do navio (m/s), d é o coeficiente de arrasto (adimensional), e A é a cross-sectional area (m2).
Note-se que a área de secção transversal não é realmente calculado no jogo. Em vez disso é Supõe-se que é directamente proporcional à massa, que é uma simplificação irrealista feita por KSP. o parâmetro FlightGlobals.Múltiplo arrastro indica que a relação de proporcionalidade é 0.008 m2/kg, assim:
onde M é a massa do navio (kg).
A densidade atmosférica ρ é diretamente proporcional à pressão atmosférica (p da unidade atm), que é uma função da altitude, a pressão da atmosfera em altitude 0 (p0), e altura escala (H):
em que p é aqui em unidades atm, e ρ em kg/m3. O fator de conversão de 1.2230948554874 kg/(m3·atm) é dado pela FlightGlobals.getAtmDensity(1.0), que retorna a densidade a 1 atmosfera (do nível do mar em Kerbin) de pressão.
O coeficiente de arrasto ( d ) é calculada como a média ponderada de massa dos valores max_drag de todas as partes na nave. Para a maioria das naves sem pára-quedas implantados, d será muito próximo de 0,2, uma vez que este é o valor max_drag da grande maioria das peças. Além disso, um grupo da mesma parte tem sempre o mesmo coeficiente de arrasto.
Como um exemplo, o coeficiente de arrasto para uma embarcação que consiste simplesmente de um Mk1-2 comando Pod (massa 4, arraste 0,2) e um implantado Mk16-XL Parachute (massa 0.3 arraste 500) é:
A velocidade terminal
A velocidade terminal de um objeto que cai através de uma atmosfera, é a velocidade a que a força da gravidade é igual à força de arrasto. Mudanças velocidade terminal em função da altitude. Com tempo suficiente, um objeto caindo na atmosfera vai desacelerar a velocidade terminal e, em seguida, permanecer em velocidade terminal para o resto de sua queda.
Velocidade terminal é importante porque é ela que descreve a quantidade de velocidade que uma nave espacial deve queimar quando estiver perto do chão, e também representa a velocidade com que uma nave deve estar viajando para cima durante uma subida de combustível ideal.
A força da gravidade (FG) é:
onde M ainda é a massa do navio, G é o constante gravitacional, M é a massa do planeta, e R é o distância do centro do planeta para o objeto em queda.
Para encontrar a velocidade terminal, montamos FG equal to FD:
Partindo do princípio de d é de 0,2 (o que é uma boa aproximação, pára-quedas previstas não estão em uso), isso simplifica a:
Para o pod Mk1-2 e exemplo de pára-quedas Mk16XL foto acima, o coeficiente de arrasto é 35,07, pelo que a sua velocidade terminal ao nível do mar em Kerbin (que é 600 & nbsp; km do centro de Kerbin) é:
Exemplos
| Altitude (m) | vT (m/s) | |||||
|---|---|---|---|---|---|---|
| Eve | Kerbin | Duna | Jool | Laythe | ||
| 0 | 58,385 | 100,13 | 212,41 | 23,124 | 115,62 | |
| 100 | 58,783 | 101,01 | 214,21 | 23,162 | 116,32 | |
| 1000 | 62,494 | 109,30 | 231,16 | 23,508 | 122,83 | |
| 10000 | 115,27 | 240,52 | 495,18 | 27,272 | 211,77 | |
On-rails de física
Se uma nave é "on rails" (ou seja, é mais do que 2.25 km a partir do navio-controlado ativamente) e sua órbita passa através da atmosfera de um planeta, uma das duas coisas vai acontecer com base na pressão atmosférica em altitude do navio:
- Abaixo de 0.01 atm: nenhum arrasto atmosférico ocorrerá e a nave será completamente afetada.
- 0.01 atm ou acima: a nave irá desaparecer.
A tabela a seguir mostra a altitude desta 0,01 atm para cada corpo celeste com uma atmosfera:
| Body | Altitude (m) |
|---|---|
| Eve | 44 745 |
| Kerbin | 25 789 |
| Duna | 10 814 |
| Jool | 219 397 |
| Laythe | 32 755 |
Altura atmosférica
A altura atmosférica depende da altura escala do corpo celestial e é onde 0.000001th (0.0001%) de a superfície de pressão está permanecendo assim a pressão atmosférica na fronteira não é constante. Tecnicamente, uma nave em órbita de Jool pode ir mais baixo para a atmosfera (ou a atmosfera começa a partir de uma pressão mais elevada).
A atmosfera de Kerbin termina em 0.000001 & nbsp; atm e calcular onde os outros corpos celestes devem ter a altura atmosférica: