Difference between revisions of "Atmosphere/fr"

Latest revision as of 10:58, 15 May 2021

La pression de toutes les atmosphères.

Planètes				Lunes
	Eve		Kerbin		Laythe
	Duna		Jool

L'atmosphère d'un corps céleste ralentit le mouvement de tout objet le traversant, par une force nommée frottements atmosphériques, ou simplement frottements. Une atmosphère permet également la portance aérodynamique. Les corps célestes du jeu avec une atmosphère sont Eve, Kerbin, Duna et Jool, ainsi que Laythe, une Lune de Jool. Seuls Kerbin et Laythe possèdent une atmosphère contenant de l'oxygène et permettant donc l'utilisation d'entrées d'air pour les réacteurs d'avion.

Les atmosphères permettent l'aérofreinage et un atterrissage plus facile. Toutefois, une atmosphère rend le décollage depuis une planète plus difficile et augmente l'altitude minimale d'orbite stable.

Données physiques

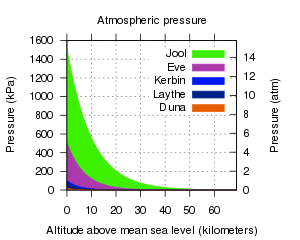
Les atmosphères ont une pression qui varie exponentiellement avec l'altitude.

${\displaystyle p=p_{0}\cdot e^{\frac {-altitude}{H}}}$

où p₀ est la pression à l'altitude 0, et H la hauteur d'échelle (m).

La hauteur d'échelle d'une atmosphère définit à quelle vitesse celle-ci diminue en pression. Dans le cas de l'atmosphère de Kerbin, elle vaut environ 5600m, c'est-à-dire que la pression est divisée par 2,718 à chaque fois que l'on monte de 5600m.

Les atmosphères varient également en température. Bien que cela ait peu d'impact sur le gameplay, cela affecte la densité atmosphérique et la vitesse du son, données utilisées dans le calcul des frottements. Avec la loi des gaz parfaits, la densité en kg/m³ se calcule comme cela:

où R est la constante spécifique du gaz, qui vaut 287.053 J/kg-K. La vitesse du son (c) est calculée par:

Notez que pour l'atmosphère de Kerbin, la température et la pression sont modélisés pour correspondre aux données terrestres en utilisant les équations de l'USSA (Atmosphère Standard US). Voir Atmosphère de Kerbin.

Frottements

Une capsule Mk1-2 avec un parachute Mk16-XL ralentie par frottements dans l'atmosphère de Kerbin.

Dans le jeu, la force des frottements atmosphériques dépend de la forme de la pièce et de quels points d'attache de la pièce sont utilisés. Par exemple, les cônes de nez réduisent les frottements de la pièce à laquelle ils sont attachés. Une option de debug permet de connaitre la valeur de la force sur une pièce en faisant un clic-droit dessus.

En général, les frottements fonctionnent avec l'équation suivante:

${\displaystyle F_{D}=0.5\,\rho \,v^{2}\,d\,A}$

où ρ est la densité atmosphérique, v est la vitesse du vaisseau (m/s), d est le coefficient de frottement (sans unité), et A est la surface frontale (m²).

Hauteur de l'atmosphère

La hauteur de l'atmosphère est l'altitude à laquelle il reste 0.0001% de la pression de surface. Ainsi, la pression à la limite de l'atmosphère est relative: un vaisseau en orbite autour de Jool peut avoir une orbite plus basse (par rapport à la surface) car la pression de surface est plus importante.

${\displaystyle alt_{\text{hauteur atmosphérique}}=-ln\left(10^{-6}\right)\cdot {\text{échelle de hauteur}}}$

${\displaystyle p_{\text{hauteur atmosphérique}}=p_{0}\cdot 10^{-6}}$

Pour calculer la hauteur de l'atmosphère d'autres corps célestes:

${\displaystyle alt_{\text{hauteur atmosphérique (vraie)}}=-ln\left({\frac {10^{-6}}{p_{0}}}\right)\cdot {\text{échelle de hauteur}}}$

Vitesse terminale

• Voir aussi: Vitesse terminale sur Wikipédia.

La vitesse terminale d'un objet en chute dans une atmosphère est la vitesse à laquelle les forces de frottements compensent le poids. La vitesse terminale dépend de l'altitude. Avec suffisamment de temps, un objet en chute dans l'atmosphère va ralentir jusqu'à la vitesse terminale puis y rester pour le reste de la chute. La vitesse terminale est importante car:

• Elle décrit la vitesse qu'un vaisseau devra freiner avec des propulseurs proche du sol.
• Elle représente la vitesse à laquelle un vaisseau devrait monter lors d'une montée économe en carburant.

Le poids (P) peut être calculé comme:

${\displaystyle P=m\cdot g=m\cdot {\frac {GM}{r^{2}}}}$

où m est la masse du vaisseau, G est la constante gravitationnelle, M est la masse de la planète, et r est la distance du centre de la planète au vaisseau. La vitesse terminale peut être trouvée en déterminant pour quelle vitesse les frottements F sont égaux au poids P.

Exemples

La vitesse terminale de pour un corps donné dépend de l'altitude dans l'atmosphère.

Physique "on-rails"

Un vaisseau est considéré "on rails" lorsqu'il n'est plus le focus premier de la simulation, c'est à dire qu'il est à plus de 2,25km du vaisseau contrôlé par le joueur. Si un tel vaisseau est dans une atmosphère, l'une de ces deux choses se passera:

• Si la pression atmosphérique est de moins de 0.01 atm, le vaisseau ne subira aucun frottement.
• Si la pression atmosphérique est supérieure à 0.01 atm, le vaisseau disparaîtra.

Ce tableau donne l'altitude limite de 0.01 atm pour chaque corps possédant une atmosphère.

Voir aussi

• Rentrée atmosphérique (en)

Notes