Difference between revisions of "Terminology/hu"
(→Manőverezés az ürben [Space Maneuvers]) |
m |
||
| (43 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
Ez a lap egy tömör szószedete a szükséges kifejezéseknek, mely segedelmével elindulhattok azon az úton amelyen zöldfülűekből képzett asztronautákká vagy rakétatudósokká válhattok! Mivel ez egy szószedet ezért a magyar kifejezés mellet megtalálhatjátok szögletes zárójelben a KSP világában található angol kifejezést is. | Ez a lap egy tömör szószedete a szükséges kifejezéseknek, mely segedelmével elindulhattok azon az úton amelyen zöldfülűekből képzett asztronautákká vagy rakétatudósokká válhattok! Mivel ez egy szószedet ezért a magyar kifejezés mellet megtalálhatjátok szögletes zárójelben a KSP világában található angol kifejezést is. | ||
| − | == Matematika == | + | == <span id="Mathematics"> Matematika </span> == |
<div style="float:right;">[[File:cartesian.svg|thumb|upright|left|Descartes-féle derékszögű koordináta-rendszer - derékszögű koordinátákat használ]][[File:polar.svg|thumb|upright|Gömbi koordináta rendszer - csak szögeket és egy hosszt használ]]</div> | <div style="float:right;">[[File:cartesian.svg|thumb|upright|left|Descartes-féle derékszögű koordináta-rendszer - derékszögű koordinátákat használ]][[File:polar.svg|thumb|upright|Gömbi koordináta rendszer - csak szögeket és egy hosszt használ]]</div> | ||
| Line 9: | Line 9: | ||
:Ovális-jellegű zárt pályagörbe, gyakran utalnak rá a pályák leírásakor. A keringő testek tipikus pályagörbéje. | :Ovális-jellegű zárt pályagörbe, gyakran utalnak rá a pályák leírásakor. A keringő testek tipikus pályagörbéje. | ||
;Hiperbolikus [Hyperbolic] | ;Hiperbolikus [Hyperbolic] | ||
| − | :Nyílt pályagörbe, a befogatlan testek tipikus | + | :Nyílt pályagörbe, a befogatlan testek tipikus pályagörbéje. |
;Normális avagy normál vektor [Normal vector] | ;Normális avagy normál vektor [Normal vector] | ||
:Egy az adott síkra merőleges egységvektor. | :Egy az adott síkra merőleges egységvektor. | ||
;Skalár [Scalar] | ;Skalár [Scalar] | ||
| − | :Egy egyszerű érték irány nélkül. A skalárokat rendszerint a mértékegység követi, mely elárulja annak dimenzióját. Például 3 m/s, 3 m,3 s a "3" a skalár az utánuk következő mértékegységek elárulják, hogy sebesség, hossz/távolság vagy idő, de mindezt irány nélkül. | + | :Egy egyszerű érték irány nélkül. A skalárokat rendszerint a mértékegység követi, mely elárulja annak dimenzióját. Például 3 m/s, 3 m, 3 s a "3" a skalár az utánuk következő mértékegységek elárulják, hogy sebesség, hossz/távolság vagy idő, de mindezt irány nélkül. |
;Vektor [Vector] | ;Vektor [Vector] | ||
:Irányok és értékek készlete. Például adott irányok és az arra mutató sebességkomponensek együtt megadják a sebességet. A vektor kifejezés függ a koordináta-rendszer fajtájától, valamint hogy mennyi dimenziót vettünk figyelembe. A <35°, 12> egy két dimenziós polár-vektor, míg a <14, 9, -20> egy háromdimenziós Descartes-féle derékszögű koordináta rendszerben értelmezhető vektor. 3 dimenzióban az előbb említett Descartes-féle derékszögű koordináta rendszer mellett gyakran alkalmazott - főleg egy bolygóhoz viszonyított helyzet megadására - a gömbi koordináta rendszer melyben két szög(szélesség, hosszúság) és a magasság adja meg a helyzetet amely egy 3 dimenziós polár koordináta-rendszer. Természetesen léteznek egyéb koordináta rendszerek, de ezek most számunkra lényegtelenek... | :Irányok és értékek készlete. Például adott irányok és az arra mutató sebességkomponensek együtt megadják a sebességet. A vektor kifejezés függ a koordináta-rendszer fajtájától, valamint hogy mennyi dimenziót vettünk figyelembe. A <35°, 12> egy két dimenziós polár-vektor, míg a <14, 9, -20> egy háromdimenziós Descartes-féle derékszögű koordináta rendszerben értelmezhető vektor. 3 dimenzióban az előbb említett Descartes-féle derékszögű koordináta rendszer mellett gyakran alkalmazott - főleg egy bolygóhoz viszonyított helyzet megadására - a gömbi koordináta rendszer melyben két szög(szélesség, hosszúság) és a magasság adja meg a helyzetet amely egy 3 dimenziós polár koordináta-rendszer. Természetesen léteznek egyéb koordináta rendszerek, de ezek most számunkra lényegtelenek... | ||
| Line 30: | Line 30: | ||
* Egy skalár hármas, amik lehetnek hosszak illetve szögek melyek meghatároznak egy helyet a koordináta rendszerben. | * Egy skalár hármas, amik lehetnek hosszak illetve szögek melyek meghatároznak egy helyet a koordináta rendszerben. | ||
| − | == Keringés kifejezései == | + | == <span id="Orbital terms"> Keringés kifejezései </span> [Orbital terms]== |
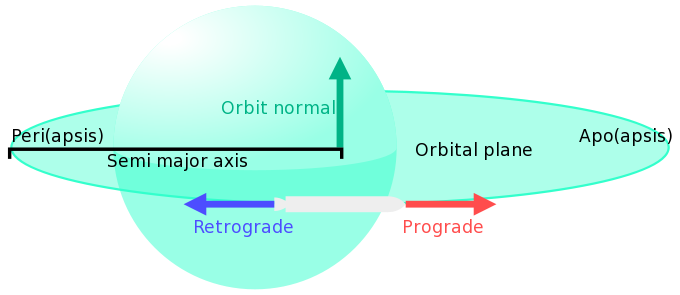
[[File:Orbit.svg|thumb|upright=2.25|A leggyakoribb pályaparaméterek szemléltetése]] | [[File:Orbit.svg|thumb|upright=2.25|A leggyakoribb pályaparaméterek szemléltetése]] | ||
| − | ;<span id="ap">Apoapszis | + | ;<span id="ap">Apoapszis</span> avagy távolpont [Apoapsis] |
| − | ;<span id="pe">Periapszis | + | ;<span id="pe">Periapszis</span> avagy közelpont [Periapsis] |
| − | ; | + | ;Apszispontok [Apsis] |
| − | {{See also|Orbit|section= | + | {{See also|Orbit/hu|section=Apoapszis és periapszis|Keringési pálya}} |
| − | :Minden elliptikus pályának két | + | :Minden elliptikus pályának két apszispontja van. A '''periapszis''' (<tt>q</tt>) (közelpont) a legközelebbi pontja a pályának (a legalacsonyabban ilyenkor van a keringő test) és az '''apoapszis''' (<tt>Q</tt>) (távolpont) amely a pálya túloldalán van és a legtávolabbi pont is egyben (a keringő test ilyenkor van a legmagasabban). Az apszisok értékeit gyakran az adott égitest felszínétől adják meg, miközben a legtöbb egyenlet számára a tömegközépponttól számított távolsággal dolgozik, így ilyenkor a felszíntől számított értékekhez hozzá kell adni a test sugarát. |
;<span id="appe">Peri-* és Apo-*</span> | ;<span id="appe">Peri-* és Apo-*</span> | ||
:Mikor pályákról beszélünk, gyakran a "periapszis" és "apoapszis" módosulnak a pálya közepén lévő égitest nevével. Például, -kee és -kerb mind gyakran használtak a Kerbin körüli pályák leírásakor, minek folytán Perikee/Perikerb és Apokee/Apokerb kifejezésekkel is találkozhatunk. | :Mikor pályákról beszélünk, gyakran a "periapszis" és "apoapszis" módosulnak a pálya közepén lévő égitest nevével. Például, -kee és -kerb mind gyakran használtak a Kerbin körüli pályák leírásakor, minek folytán Perikee/Perikerb és Apokee/Apokerb kifejezésekkel is találkozhatunk. | ||
| − | ;<span id="an">Felszálló csomó [Ascending node] | + | ;<span id="an">Felszálló csomó</span> [Ascending node] |
| − | :Az a pont amelynél a pálya észak felé haladva metszi a referenciasíkot. Itt, "észak" a referenciasík normálisát jelenti. | + | :Az a pont ([[#on|pályacsomó]]) amelynél a pálya észak felé haladva metszi a referenciasíkot. Itt, "észak" a referenciasík normálisát jelenti. |
| − | ;<span id="dn">Leszálló csomó [Descending node] | + | ;<span id="dn">Leszálló csomó</span> [Descending node] |
| − | :Az a pont ahol a a pálya délfelé haladva metszi a referencia síkot. | + | :Az a pont ([[#on|pályacsomó]]) ahol a a pálya délfelé haladva metszi a referencia síkot. |
| − | ;<span id="ecc">Excentricitás | + | ;<span id="ecc">Excentricitás avagy a pálya elnyújtottsága</span> [Eccentricity] |
:Egy skalár amely kifejezi a pálya körtől való eltérését . | :Egy skalár amely kifejezi a pálya körtől való eltérését . | ||
<math style="float:center;padding:0.5em;">\text{ecc} = 1 - \frac{2}{\frac{Q}{q}+1}</math> | <math style="float:center;padding:0.5em;">\text{ecc} = 1 - \frac{2}{\frac{Q}{q}+1}</math> | ||
| Line 50: | Line 50: | ||
:* ecc = 1 → parabolikus pálya - ez szökési pálya. | :* ecc = 1 → parabolikus pálya - ez szökési pálya. | ||
:* ecc > 1 → hiperbolikus pálya - ez is szökési pálya. | :* ecc > 1 → hiperbolikus pálya - ez is szökési pálya. | ||
| − | ;<span id="inc"> | + | ;<span id="inc"> Inklináció avagy pályahajlás</span> [Inclination] |
:A pályasík és a referenciasík által bezárt szög. (megjegyzés az egyenlítő síkjával 90°-ot bezáró pályát poláris-nak nevezik) | :A pályasík és a referenciasík által bezárt szög. (megjegyzés az egyenlítő síkjával 90°-ot bezáró pályát poláris-nak nevezik) | ||
;<span id="lo">Alacsony pálya [Low orbit]</span> | ;<span id="lo">Alacsony pálya [Low orbit]</span> | ||
| − | : Egy stabil és biztonságos pálya amely csak éppen annyira magas, hogy elkerülje a veszélyeket, mint a légkörben való lefékeződést vagy éppen a hegyeknek való ütközést. Az alacsony pálya egy lépcsőfok amely a felemelkedés után várakozhatunk, hogy egy gyorsítással találkozhassunk egy másik járművel vagy égitesttel, vagy éppen az ellenkező irányban a legkevesebb üzemanyag felhasználásával szállhassunk le. A légkörrel rendelkező égitestek esetén, mint amilyen a [[Kerbin]] ez a közvetlenül a légkör feletti részt jelenti(70km-100km). A légkör nélküli égitesteknél ez elméletileg bármely felszín feletti magasság lehetne, de egy magasság alatt már a hegyek és magaslatok veszélyeztetik a pályát. Ilyenkor nem árt tudni a magaslatokról! Az | + | : Egy stabil és biztonságos [[orbit/hu|keringési pálya]] amely csak éppen annyira magas, hogy elkerülje a veszélyeket, mint a légkörben való lefékeződést vagy éppen a hegyeknek való ütközést. Az alacsony pálya egy lépcsőfok amely a felemelkedés után várakozhatunk, hogy egy gyorsítással találkozhassunk egy másik járművel vagy égitesttel, vagy éppen az ellenkező irányban a legkevesebb üzemanyag felhasználásával szállhassunk le. A légkörrel rendelkező égitestek esetén, mint amilyen a [[Kerbin/hu|Kerbin]] ez a közvetlenül a légkör feletti részt jelenti (70km-100km). A légkör nélküli égitesteknél ez elméletileg bármely felszín feletti magasság lehetne, de egy magasság alatt már a hegyek és magaslatok veszélyeztetik a pályát. Ilyenkor nem árt tudni a magaslatokról! Az [[time warp/hu|időgyorsítás]] [time warp] korlátozva van az alacsony pályán, és lehetetlen az alatt. |
| − | ;<span id="node">Pályacsomók [Orbital nodes] | + | ;<span id="on">Pályacsomó</span> ''(csillagászati definíció)'' |
| − | :Bármely pályán lévő specifikus referenciapontok mint az Apoapszis, Periapszis, vagy a más pályákkal való metszéspontok[intersect points]. | + | :Egy pont ahol a pálya keresztezi a referenciasíkot. A felszálló csomó esetében a test a referenciasík pályanormálisának irányában halad. A felszálló irány "észak", míg a leszálló irány "dél" felé mutat. |
| − | ;<span id="orbnorm">Pályanormális [Orbit normal] | + | ;<span id="node">Pályacsomók</span> [Orbital nodes] ''(a játékban)'' |
| − | :A pályasík normálisa. Ezt a hajó | + | :Bármely pályán lévő specifikus referenciapontok mint az Apoapszis, Periapszis, vagy a más pályákkal való metszéspontok [intersect points]. |
| − | ;<span id="orbplane">Pályasík [Orbital plane] | + | ;<span id="orbnorm">Pályanormális</span> [Orbit normal] |
| + | :A pályasík normálisa. Ezt a hajó sebességének és az égitest gravitációjának a vektoriális szorzata adja. Mivel ez a jobb-kéz szabályt követi, olyan nézőpontból, ahonnan a hajó pozitív(az órajárással ellentétes) irányba kering felfelé(a szemlélő felé), ellenkező esetben pedig lefelé(a szélélőtől el) fog mutatni. A "Fel" ["Up"] gyakran mint "észak" [North] or "N+", és a párja mint "Le" ["Down"] másként "Anti-Normál" ["Anti-Normal"] avagy "Dél" ["South"] vagy "N-" van jelölve. | ||
| + | ;<span id="orbplane">Pályasík</span> [Orbital plane] | ||
:Egy sík, melyet a keringés pályája feszít ki. | :Egy sík, melyet a keringés pályája feszít ki. | ||
| − | ;<span id="prograde">Prográd | + | ;<span id="orbspeed">Pályasebesség</span> [Orbital speed] |
| − | :Az az irány amely felé a test halad a pályája mentén. Elliptikus pálya esetén ez mindig a test tartózkodási helyén vett érintő iránya. | + | :Egy test pályasebessége az a sebesség amellyel a vizsgált rendszer középpontja körül kering, általában egyszerűen nézve a nagyobb test körül. A pályasebességet lehet értelmezni mint átlag-pályasebességet, amellyel megteszi a körülkeringést, vagy a sebesség a pálya egy adott pontján. |
| − | ;<span id="retrograde">Retrográd | + | ;<span id="prograde">Prográd</span> [Prograde] |
| − | :A prográd ellentetje, | + | :Az az irány amely felé a test halad a pályája mentén. Elliptikus pálya esetén ez mindig a test tartózkodási helyén vett érintő iránya. Menetirányt. |
| − | ;<span id="refplane">Referenciasík [Reference plane] | + | ;<span id="retrograde">Retrográd</span> [Retrograde] |
| − | :Bármely sík, amelyet az aktuális pálya leírásakor viszonyítási alapként felhasználunk. A bolygók körüli pályák esetén ez többnyire az egyenlítő síkja. Több test esetén az ellipszis síkját használhatják. Egy másik keringő test befogása esetén a befogandó test pályasíkját használják. Egy pályasíkot teljesen leír egy referenciasíkhoz viszonyított pályahajlás és a felszálló csomó hosszúsági szöge[longitude]. | + | :A prográd ellentetje, a pályán haladási iránnyal szemben. Menetiránnyal szemben. |
| − | ;<span id="sma">Fél nagytengely [Semi-major axis] | + | ;<span id="refplane">Referenciasík</span> [Reference plane] |
| − | <math class="float | + | :Bármely sík, amelyet az aktuális pálya leírásakor viszonyítási alapként felhasználunk. A bolygók körüli pályák esetén ez többnyire az egyenlítő síkja. Több test esetén az ellipszis síkját használhatják. Egy másik keringő test befogása esetén a befogandó test pályasíkját használják. Egy pályasíkot teljesen leír egy referenciasíkhoz viszonyított pályahajlás és a felszálló csomó hosszúsági szöge [longitude]. |
| − | + | ;<span id="sma">Fél nagytengely</span> [Semi-major axis] | |
| − | :A nagy | + | {{See also|Orbit/hu|section=Fél nagytengely|Keringési pálya}} |
| − | ;<span id="suborb">Szuborbitális [Sub-orbital] | + | <math class="float">\text{a} = \text{R} + \frac{Q+q}{2}</math> |
| + | :A nagy tengely a hosszú tengelye az ellipszisnek a fél nagytengely (<tt>a</tt>) ennek a fele. Az apoapszis (<tt>Q</tt>) és a periapszis (<tt>q</tt>) átlagját középponthoz viszonyítva számítjuk. Mivel mindkettő a felszínhez viszonyított érték, egyszerűen hozzáadjuk az égitest sugarát (<tt>R</tt>). Egy égitest körül minden azonos fél nagytengellyel rendelkező pályának azonos keringési ideje van, függetlenül az excentricitástól. | ||
| + | ;<span id="sidereal period">Csillagászati keringési idő</span> [Sidereal period] | ||
| + | :A csillagászati keringési idő (gyakran csak mint keringési idő, de ismert mint sziderikus keringési idő is) az az időciklus amely alatt a keringő test megtesz egy teljes körülkeringést a csillagokhoz viszonyítva. Ezt a keringési ciklust egy inerciarendszerhez (amely nem forog) viszonyítjuk. | ||
| + | ;<span id="suborb">Szuborbitális</span> [Sub-orbital] | ||
:Olyan pálya, amelynél a periapszis az égitest felszíne alatt található. A szuborbitális pályát követve a keringő test szükségszerűen beleütközik az égitestbe. | :Olyan pálya, amelynél a periapszis az égitest felszíne alatt található. A szuborbitális pályát követve a keringő test szükségszerűen beleütközik az égitestbe. | ||
| + | ;<span id="synodic period">Szinodikus keringési idő</span> [Synodic period] | ||
| + | :A szinodikus keringési idő az az időtartam, amennyi ideig tart, hogy egy test újra megjelenjen egy két vagy több testhez viszonyított ugyanazon ponton, pl. a [[Mun/hu|Mün]] helyzete a [[Kerbol/hu|Kerbol]]hoz képest ahogy a [[Kerbin/hu|Kerbin]]-ről figyelve visszatér ugyanarra a megvilágítási helyzetbe (holdtölték közti idő). A szinodikus keringési idő az az idő amely eltelik két egymást követő Kerbol–Kerbin vonallal azonos sorrendben történő találkozás (együttállás) között. A szinodikus keringési periódus különbözik a csillagászati keringési periódustól, mivel maga a Kerbin is kering a Kerbol körül. | ||
| − | == Hajó irányultsága [Ship Orientation] == | + | <span id="Ship Orientation"></span> |
| + | |||
| + | == <span id="Hajó irányultsága"> Hajó irányultsága </span> [Ship Orientation] == | ||
A hajó irányultsága mindig egy kiválasztott testhez kötődik. Ez többnyire a kabin. | A hajó irányultsága mindig egy kiválasztott testhez kötődik. Ez többnyire a kabin. | ||
;Zenit [Zenith] | ;Zenit [Zenith] | ||
| Line 88: | Line 98: | ||
:Hátsó oldala a hajónak, mely többnyire a főrakéták otthona és retrogád mutat. Az eleje ellentettje. | :Hátsó oldala a hajónak, mely többnyire a főrakéták otthona és retrogád mutat. Az eleje ellentettje. | ||
| − | + | <span id="Space Maneuvers"></span> | |
| − | + | == <span id="Pályamódosítások"> Pályamódosítások</span> [Space Maneuvers] == | |
| − | + | ||
| − | + | ;Levegőfékezés avagy légköri fékezés [Atmospheric braking] [Aerobraking] | |
| − | ;Levegőfékezés [Atmospheric braking][Aerobraking] | + | {{Main article|Aerobraking/hu|Levegőfékezés}} |
| − | {{Main article|Aerobraking}} | + | :Egy égitest felső-[[Atmosphere/hu|légkörébe]] lépve a légellenállás segítségével az űreszköz veszít a mozgási energiájából, aminek következtében a sebességcsökkenés mellett a hiperbolikus pályagörbén érkező eszköz elliptikus pályára állhat, illetve az elliptikus pályán keringő test apoapszisa is csökken - kisebb értékben a periapszisa is. Okosan alkalmazva a pályamódosítások során ezzel a manőverrel jelentős mértékben csökkenthető az üzemanyag-felhasználás. Viszont ez az alsóbb légkörbe való belépéshez is vezethet, amely során a jelentős lassulás végül az égitestre kényszeríti az eszközt. Ügyelni kell a manőver során, hogy a légellenállás során a súrlódás miatt keletkező hő és erőhatások ne károsítsák az eszközt (A KSP-ben Jelenleg csak DRE mod esetén)! |
| − | :Egy égitest felső-légkörébe lépve a légellenállás segítségével az űreszköz veszít a mozgási energiájából, aminek következtében a sebességcsökkenés mellett a hiperbolikus pályagörbén érkező eszköz elliptikus pályára állhat, illetve az elliptikus pályán | + | ;<span id="atmospheric entry">Belépés a légkörbe</span> [Atmospheric entry] |
| − | ;<span id="atmospheric entry">Belépés a légkörbe [Atmospheric entry] | + | {{Main article|Atmospheric entry/hu|Belépés a légkörbe}} |
| − | {{Main article|Atmospheric entry}} | + | :A légkörbe való belépéskor a légellenállást felhasználva felszínt keresztező pályára lassítjuk az eszközt. Ez jelentős mechanikai- és hőterhelést jelent az eszköz számára, amely az eszköz szétszakadásához, vagy [[Overheating/hu|túlhevüléséhez]] [overheat] vezethet. Túl kis belépési szög esetén az eszköz visszapattan a légkörről a világűrbe (nincs megvalósítva, nincs mod). A légkörbe való belépést gyakran gyakran mint visszatérés a légkörbe vagy egyszerűbben visszatérés [re-entry/reentry] említik, de ez elméletben csak Kerbin atmoszférájába való visszatérésnél igaz (és feltéve, ha nem idegenek lépnek a kis zöld barátaink légkörébe); A légörbe való belépés általánosabb kifejezés. |
| − | :A légkörbe való belépéskor a légellenállást felhasználva felszínt keresztező pályára lassítjuk az eszközt. Ez jelentős mechanikai- és hőterhelést jelent az eszköz számára | + | ;Gyorsítás avagy égetés [Burn] |
| − | ;Gyorsítás avagy | ||
:A hajtóművek használata, általában a pályamódosítás céljából. | :A hajtóművek használata, általában a pályamódosítás céljából. | ||
;Körpályára állás [Circularizing] | ;Körpályára állás [Circularizing] | ||
:Egy manőver, melynek során az elliptikus pályát kör alakúra módosítjuk, azaz a pálya excentricitását 0, vagy legalábbis közel 0 szintre csökkentjük. Ezt általában az apszisoknál történő gyorsítással lehet elérni. | :Egy manőver, melynek során az elliptikus pályát kör alakúra módosítjuk, azaz a pálya excentricitását 0, vagy legalábbis közel 0 szintre csökkentjük. Ezt általában az apszisoknál történő gyorsítással lehet elérni. | ||
| − | ; | + | ;Hintamanőver, gravitációs parittya [Gravity assist] |
| − | {{Main article|Maneuver node}} | + | {{Main article|Gravity assist/hu|Hintamanőver}} |
| + | :Olyan manőver, amelynél a keringő égitest tömegvonzását használjuk ki a pályamódosításhoz vagy az űrjárművünk sebességének üzemanyag-takarékos megváltoztatására, ezzel jelentős (több száz m/s-nyi [[Delta-v/hu|Δv]]) megtakarítást érve el. Az elve szerint gyorsításnál a keringő test mögé, lassításkor a keringő test elé kell célozni. | ||
| + | ;;<span id="Lithobraking">Földfékezés</span> [Lithobraking] | ||
| + | :→ Lásd még: ''[[w:hu:Földfékezés|Földfékezés]]'' | ||
| + | :Olyan leszállási manőver, amelyben a leszállás kis szögben történik és légzsákkal védve a leszálló eszközt az kigurulva veszti el a sebességét. Bizonyos estekben a kifejezést az eszköz felszínhez csapódásával történő szándékos megsemmisítésére is használják. Az angol nyelvű elnevezés ''aerobraking''-ből lett ferdítve, ahol ''areo'' lecserélték a görög ''lithos'' szóra amely követ jelent. | ||
| + | ;<span id="Maneuver node">Manővercsomó</span> [Maneuver node] | ||
| + | {{Main article|Maneuver node/hu|Manővercsomó}} | ||
:A manőver csomók kellemes eszközei a pályamódosítások megtervezésének és végrehajtásának, mivel a manőver megkezdése előtt láthatóvá válik az adott gyorsítással létrejövő pályamódosulás. | :A manőver csomók kellemes eszközei a pályamódosítások megtervezésének és végrehajtásának, mivel a manőver megkezdése előtt láthatóvá válik az adott gyorsítással létrejövő pályamódosulás. | ||
| + | ;Sugárirányú gyorsítás [Radial burn] | ||
| + | {{See also|#Maneuver node|Manővercsomó}} | ||
| + | ;Sugárirányú befelé gyorsítás [Radial-in burn] | ||
| + | :Az égitest középpontja felé történő gyorsítás. Elfogatja a pályát a keringés irányába amíg a periapszis nem éri el az égitest tömegközéppontját. A sugárirányú kifelé gyorsítás ellentettje. | ||
| + | ;Sugárirányú kifelé gyorsítás [Radial-out burn] | ||
| + | :Az égitest középpontjától kifelé történő gyorsítás. Elfogatja a pályát a keringés iránnyal ellentétesen amíg a periapszis át nem halad tömegközéppontján. A sugárirányú befelé gyorsítás ellentettje. | ||
;Visszatérés [Re-entry] | ;Visszatérés [Re-entry] | ||
| − | {{See also|#atmospheric entry| | + | {{See also|#atmospheric entry|Belépés a légkörbe}} |
;Lassítás avagy ellenégetés [Retroburn] | ;Lassítás avagy ellenégetés [Retroburn] | ||
:Olyan gyorsítás amelyet "visszafelé"[backwards] hajtanak végre, azaz a hajtóművek prográd az orr pedig retrográd néznek. Ez az egyszerű manőver a csökkenti pálya magasságát, miközben a pálya egyéb paramétereit nem befolyásolja. | :Olyan gyorsítás amelyet "visszafelé"[backwards] hajtanak végre, azaz a hajtóművek prográd az orr pedig retrográd néznek. Ez az egyszerű manőver a csökkenti pálya magasságát, miközben a pálya egyéb paramétereit nem befolyásolja. | ||
| − | == Fizika == | + | == <span id="Physics"> Fizika </span> == |
;Gyorsulás [Acceleration] | ;Gyorsulás [Acceleration] | ||
| − | :A sebességváltozás gyorsasága. A gyorsulás vektor jellegű mennyiség, mértékegysége | + | :A sebességváltozás gyorsasága. A gyorsulás vektor jellegű mennyiség, mértékegysége: m/s<sup>2</sup>. |
;Ballisztikus pálya [Ballistic trajectory] | ;Ballisztikus pálya [Ballistic trajectory] | ||
| − | :Egy zuhanó test pályagörbéje ballisztikus. | + | :Egy zuhanó test pályagörbéje ballisztikus. Ez lényegében annyit tesz, hogy az adott testre lényegében csak a gravitáció ereje hat és nincs kitéve egyéb erőknek, mint amilyen a saját hajtómű vagy fékernyő jelentenének. |
| − | ;Delta-v (Δv) | + | ;<span id="Delta-v">Delta-v</span> (Δv) |
| − | : | + | :A sebességváltozás mértéke amelyet a saját készletéből egy impulzus elven működő jármű képes végrehajtani. Ez sebesség jellegű mennyiség, amely mértékegysége: m/s. A több teher csökkenti a delta-v-t, míg a több üzemanyag növeli. Ez hasznos, mikor egy jármű hatékonyságát akarjuk számolni és jellemezni. Például egy [[Kerbal Space Center/hu|Kerbál Ürközpont]] [[Launch pad/hu|kilövőállásáról]] [Launch pad] indított járműnek mintegy 4500 m/s-nyi delta-v-re van szüksége ahhoz, hogy biztonságosan kilépjen a [[Kerbin/hu|Kerbin]] légköréből és stabil pályára álljon a bolygó körül. |
| − | ;Energy | + | :definíciószerűen: <math>\Delta{v} = \int_{t_0}^{t_1} {\frac {|T|} {m}}\, dt</math> |
| + | :ahol ''T'' az aktuális tolóerő [thrust] ''m'' az aktuális tömeg [mass] | ||
| + | Ha feltételezzük, hogy nincs külső erő, és nem váltunk irányt, akkor sebességkülönbséget kapunk: | ||
| + | : <math>\Delta{v} = \int_{t_0}^{t_1} {\frac {|T|} {m}}\ dt = \int_{t_0}^{t_1} {|a|}\ dt = | {v}_1 - {v}_0 |\,</math> | ||
| + | Ha ezt a fajlagos impulzussal fejtjük ki akkor az eredmény: | ||
| + | : <math>\Delta{v} = | {v}_1 - {v}_0 |_{max}\ = -\int_{t_0}^{t_1} {I_{sp} \cdot g\ \cdot \frac{\dot{m}} {m}}\ dt = {I_{sp} \cdot g \cdot ln( \frac {m_0} {m_1})}\,</math> | ||
| + | |||
| + | ;<span id="Energy">Energia</span> [Energy] | ||
{{See also||{{Wikipedia|Specific orbital energy}}}} | {{See also||{{Wikipedia|Specific orbital energy}}}} | ||
| − | : | + | :A keringő test energiája a helyzeti(potenciális) és mozgási(kinetikus) energiájának az összege. |
| − | : | + | |
| − | : | + | A helyzeti energia: <math>E_p = -\frac{G M m}{R}</math> és a mozgási energia: <math>E_k = \frac{1}{2} m v^2</math> |
| − | ;Escape Velocity | + | |
| − | : | + | ahol a ''G'' a [[w:hu:Gravitációs állandó|gravitációs állandó]] [gravitational constant], ''M'' a [[celestial body/hu|égitest]] [celestial body] tömege, ''m'' a keringő [[craft/hu|űrjármű]] [craft] tömege, ''R'' a tömegközéppontjaik közötti távolság és is ''v'' a sebesség. |
| − | ;g-force ( | + | |
| − | :A | + | Ez szerint a teljes energia: <math>E = E_k + E_p = \frac{1}{2} m v^2 - \frac{G M m}{R}</math> |
| − | ;Gravity | + | |
| − | : | + | Ez az összeg nem változik, ha nincs légellenállás vagy nem működnek a hajtóművek: A periapszis felé haladva helyzeti energia mozgási energiává alakul át, a periapszison áthaladva pedig mozgási energia alakul vissza helyzeti energiává. Ha az energia vagy a fajlagos pályaenergia pozitív, akkor a test szökési pályagörbén van. |
| − | ;Gravity Well | + | :Ez az alaptézise a Kepler-féle bolygómozgás törvénynek, amely alapja a KSP közelítő módszerének. Egy ellipszis olyan pontok halmaza amelyeknek két adott ponttól - a fókuszoktól - vett távolságok összege állandó. Az egyik fókusza a Kepler-pályának a körülkeringett test tömegközéppontja, ahogy egy test megközelíti, az a helyzeti energiáját mozgási energiára váltja. Ahogy a test távolodik a körülkeringett testtől, mivel elliptikus pályáról van szó, ugyanilyen mértékben közelíti meg a másik fókuszt, ezzel a mozgási energiáját helyzeti energiára váltja. Ha a jármű egyenesen az égitest felé vagy felől halad, a fókuszok egybeesnek az apszispontokkal, ahol a mozgási (apoapszis) vagy helyzeti (periapszis) energia nulla. Ha a pálya tökéletes kör (mint a [[Mun/hu|Mün]] pályája a [[Kerbin/hu|Kerbin]] körül), a két fókusz egybeesik és a tengelyek helye határozatlan, mivel a pálya minden pontja apszisnak vehető. |
| − | : | + | |
| − | ;Orbit | + | :Van a fajlagos pályaenergia (<math>\epsilon</math>) mely nem igényli a jármú tömegének ismeretét: |
| − | {{Main article|Orbit}} | + | |
| − | : | + | <math>E_p = \epsilon_p m</math>, <math>E_k = \epsilon_k m</math>, <math>E = \epsilon \, m = (\epsilon_k + \epsilon_p) m = -\frac{G M}{2 a}</math> |
| − | ;<span id="isp">Specific Impulse (I<sub>sp</sub>)</span> | + | |
| − | {{Main article|Specific impulse}} | + | Minden azonos fél nagytengellyel(''a'') rendelkező pályának azonos a fajlagos pályaenergiája. |
| − | :<math style="float: | + | |
| − | : | + | ;<span id="Escape Velocity">Szökési sebesség</span> [Escape Velocity] |
| − | ;<span id="soi">Sphere of influence</span> | + | :Az a sebesség, mely egy adott égitest felszínéről indulva a gravitációs hatásának legyőzéséhez szükséges. |
| − | {{Main article|Sphere of influence}} | + | |
| − | : | + | Meghatározható: <math>v_e = \sqrt{\frac{2GM}{r}}</math> |
| − | ;Tangential velocity | + | |
| − | : | + | ahol a G is the [[w:hu:Gravitációs állandó|gravitációs állandó]], M az égitest tömege, r az adott égitest sugara. |
| − | ;Trajectory | + | ;g-erő avagy g-hatás [g-force] (g) |
| − | :A | + | :A gyorsulás értékét a Föld tengerszinten vett nehézségi gyorsulásának értékével kifejezve. 1 g hozzávetőleg 9,81 m/s². Egy test a Föld felszínén 1 g gyorsulásnak megfelelő hatást szenved el. A test súlya duplája 2 g gyorsulásnál és súlytalan 0 g gyorsulás esetén. Szabad esésben, mint mint amilyen a keringési pályán van légellenállás és hajtómű használata nélkül nem tapasztalható gyorsulás, amit úgy fejezhetünk ki, hogy 0 g. |
| − | ;Velocity | + | ;Gravitáció avagy tömegvonzás [Gravity] |
| − | : | + | :Minden egyes test tömegéből származó erőhatás. Roppant gyenge. Többnyire csak nagyon nagy tömegű testek mint csillagok, bolygók és holdak fejtenek ki érezhető hatást vele. Az erőhatás nagysága a tömegközéppontól számított távolság négyzetével arányosan csökken. Azaz egy kétszer távolabbi testre 1/2<sup>2</sup> = 1/4 gravitációs erő hat. |
| + | ;Gravitációs mező [Gravity Well] | ||
| + | :Az égitest körüli annak gravitációs hatása alatt álló tér. Lényegében a végtelenségig tart, de a gravitáció a távolsággal négyzetesen csökken (kétszeres távolságra a gravitáció csak negyede), így csak a hatásgömbön belül jelentős. Valójában a KSP nem szimulálja a gravitációt az égitestek hatásgömbjén kívül, mivel "foltozott kúpos közelítés"-t használ. | ||
| + | ;Keringési pálya avagy pálya [Orbit] | ||
| + | {{Main article|Orbit/hu|Pálya}} | ||
| + | :Ha egy testnek elégséges tangenciális sebessége van (és a légkörön kívül, hogy a légellenállás nem fékezheti le), akkor az a folytonosan a bolygó "mellé" esik és így sose ér földet akkor ezt a pályagörbét orbitális pályának, vagy röviden pályának nevezzük. A stabil keringési pályák elliptikusak (a kör egy nulla excentricitású ellipszis). Ha a test tangenciális sebessége meghaladja a szökési sebességet a pálya hiperbolikus lesz (határértéken parabolikus). | ||
| + | ;<span id="isp">Fajlagos impulzus [Specific Impulse] (I<sub>sp</sub>)</span> | ||
| + | {{Main article|Specific impulse/hu|Fajlagos impulzus}} | ||
| + | :<math style="float:center">I_{sp}= \frac{T}{\dot m}</math><span style="padding:1em;"></span><math style="float:center">[I_{sp}] = \frac{m}{s}</math> | ||
| + | :Az I<sub>sp</sub> kifejezi egy impulzus elven működő hatómű hatékonyságát. A magasabb I<sub>sp</sub> nagyobb fajlagos lendületváltozást azaz sebességváltozást ér el azonos tömegű üzemanyag felhasználásával. A I<sub>sp</sub> mértékét többnyire másodpercben adják meg ("s"), de fizikailag helyes mértéke a "távolság/idő" amely mértékegysége a m/s. A sebesség mértékéből származó zavart elkerülendő a fizikailag helyes I<sub>sp</sub> ("távolság/idő")-t elosztották a Föld felszíni nehézségi gyorsulásával (9,81 m/s²). Az eredmény "másodperc" ["second"] mértékegységű. Hogy használhassuk ezt a I<sub>sp</sub> az egyenletekben, vissza kell alakítanunk "távolság/idő" mértékegységűvé a Földi felszíni gyorsulással való beszorzással. Mivel itt a felszíni gyorsulással való szorzás csak a két mértékegység közti átváltásra szolgál a fajlagos impulzus független a gravitáció aktuális nagyságától. | ||
| + | :Mivel a fajlagos impulzus a tolóerő és a fajlagos üzemanyagfelhasználás hányadosa néha a következő mértékegységben adják meg: <math>\frac{Ns}{kg}</math> | ||
| + | Ez matematikailag egy másik formája a <math>\frac{m}{s} = kg \cdot \frac{m}{s^2} \cdot \frac{s}{kg}</math>-nak mivel az erő a tömeg és a gyorsulás szorzata <math>N = kg \cdot \frac{m}{s^2}</math> <span style="padding:.5em;"></span>Így valójában <math>1 \frac{Ns}{kg} = 1 \frac{m}{s}</math> egyszerű az SI alapegységekkel kifejezve. | ||
| + | ;<span id="soi">Hatásgömb, hatássugár, vonzáskör [Sphere of influence]</span> | ||
| + | {{Main article|Sphere of influence/hu|Hatásgömb}} | ||
| + | :Az a tér illetve sugár az égitest körül, amelyen belül az adott égitest gravitációs hatása a meghatározó. Jelölése: SoI/SOI. | ||
| + | ;Érintőirányú sebesség [Tangential velocity] | ||
| + | :A sebesség azon komponense, amelyik érintőirányú a pályagörbére. Pillanatnyi sebesség - az a sebesség amikor a mérési idő a nullához közelít - Ez mindig érintőleges a pályagörbére. | ||
| + | ;<span id="TWR">Tolóerő–súly arány [Thrust-to-weight ratio]</span> | ||
| + | {{Main article|Thrust-to-weight ratio/hu|Tolóerő-súly arány}} | ||
| + | :<math style="float:center;padding:.5em;">\text{TWR} = \frac{T}{W} = \frac{T}{m \cdot g}</math> | ||
| + | A jármű/fokozat aktuális tömegének és a rendelkezésre álló tolóerő aránya. Ha a tolóerő–súly arány (TWR) nagyobb mint 1, akkor a járműnek elég tolóereje van hogy felfelé gyorsulva növelje a magasságát. Az 1 alatti tolóerő–súly arány (TWR) a jármű nem tud a gravitáció ellenében haladni alacsony magasságnál, viszont az űrben mindössze hosszabb ideig tartó manővereket jelent. Mivel a súly(W) függ az égitest gravitációjától (g) a tolóerő–súly arány (TWR) függ az adott égitesttől. A felszíni gyorsulás a [[Mun/hu|Mün]] felszínén mindössze 16,6%-a [[Kerbin/hu|Kerbin]]ének, így a felszínen a tolóerő–súly arány: TWR<sub>Kerbin</sub> = 1-ről TWR<sub>Mün</sub> = 6-ra változik. | ||
| + | ;Pályagörbe [Trajectory] | ||
| + | :A pályagörbe az az útvonal, amelyet a mozgó test az idő függvényében bejár. | ||
| + | ;Sebesség [Velocity] | ||
| + | :A helyzetváltozás gyorsasága. A sebesség vektor jellegű mennyiség, azaz van mértéke és iránya. Mértékegysége: m/s. | ||
| − | == | + | ==Lásd még== |
| − | * [[Tutorials]] | + | <references /> |
| − | * [[ | + | * [[Tutorials/hu|Oktatás]] |
| + | * [[Abbreviations and acronyms/hu|Rövidítések és Jelölések]] | ||
Latest revision as of 11:29, 25 October 2015
A KSP-ben sok fizikára és pályák leírására vonatkozó kifejezés található, melyek zavaróak lehetnek a hozzá nem értőek számára, valamint egyéb változatos tudományos kifejezések és rövidítések melyekkel leírják a közkifejezéseket.
Ez a lap egy tömör szószedete a szükséges kifejezéseknek, mely segedelmével elindulhattok azon az úton amelyen zöldfülűekből képzett asztronautákká vagy rakétatudósokká válhattok! Mivel ez egy szószedet ezért a magyar kifejezés mellet megtalálhatjátok szögletes zárójelben a KSP világában található angol kifejezést is.
Contents
Matematika
- Elliptikus [Elliptical]
- Ovális-jellegű zárt pályagörbe, gyakran utalnak rá a pályák leírásakor. A keringő testek tipikus pályagörbéje.
- Hiperbolikus [Hyperbolic]
- Nyílt pályagörbe, a befogatlan testek tipikus pályagörbéje.
- Normális avagy normál vektor [Normal vector]
- Egy az adott síkra merőleges egységvektor.
- Skalár [Scalar]
- Egy egyszerű érték irány nélkül. A skalárokat rendszerint a mértékegység követi, mely elárulja annak dimenzióját. Például 3 m/s, 3 m, 3 s a "3" a skalár az utánuk következő mértékegységek elárulják, hogy sebesség, hossz/távolság vagy idő, de mindezt irány nélkül.
- Vektor [Vector]
- Irányok és értékek készlete. Például adott irányok és az arra mutató sebességkomponensek együtt megadják a sebességet. A vektor kifejezés függ a koordináta-rendszer fajtájától, valamint hogy mennyi dimenziót vettünk figyelembe. A <35°, 12> egy két dimenziós polár-vektor, míg a <14, 9, -20> egy háromdimenziós Descartes-féle derékszögű koordináta rendszerben értelmezhető vektor. 3 dimenzióban az előbb említett Descartes-féle derékszögű koordináta rendszer mellett gyakran alkalmazott - főleg egy bolygóhoz viszonyított helyzet megadására - a gömbi koordináta rendszer melyben két szög(szélesség, hosszúság) és a magasság adja meg a helyzetet amely egy 3 dimenziós polár koordináta-rendszer. Természetesen léteznek egyéb koordináta rendszerek, de ezek most számunkra lényegtelenek...
- <35°, 12> olyan mint egy 12 egység hosszú nyíl, amely az origóból indul ki és az alapvonallal bezáró 35°-os szög irányába mutat. Az alapvonal tipikusan az x-tengely és a szögeltolás az óramutatóval ellentétes irányba mutat.
- <14, 9, -20> olyan mint egy nyíl amelyik a kiindulási pontból(origóból)(<0,0,0>) kiindulva egy olyan pontban végződik amelynek az x koordinátája 14, az y koordinátája 9 és a z koordinátája -20.
- Descartes-féle derékszögű koordináta rendszer előnye, hogy pontosan megmutatja a végpont helyét, de nem ad közvetlen információt a vektor hosszáról, a polár koordináta rendszerben magától adódik a vektor hossza, de a végpont helyének meghatározása már nem olyan egyszerű.
- A következő fizikai mennyiségek mind vektorok: sebesség, gyorsulás, erő
Egy 3D koordináta rendszerhez az alábbiak kellenek:
- Egy referencia pont. Ez a kiindulási pont.
- 3 bázisvektorok. Ezek meghatározzák az alapértékét a tengelyirányú viszonyításnak és magát az adott tengelyt.
- Egy skalár hármas, amik lehetnek hosszak illetve szögek melyek meghatároznak egy helyet a koordináta rendszerben.
Keringés kifejezései [Orbital terms]
- Apoapszis avagy távolpont [Apoapsis]
- Periapszis avagy közelpont [Periapsis]
- Apszispontok [Apsis]
- → Lásd még: “Apoapszis és periapszis” bekezdést a következő cikkből: Keringési pálya
- Minden elliptikus pályának két apszispontja van. A periapszis (q) (közelpont) a legközelebbi pontja a pályának (a legalacsonyabban ilyenkor van a keringő test) és az apoapszis (Q) (távolpont) amely a pálya túloldalán van és a legtávolabbi pont is egyben (a keringő test ilyenkor van a legmagasabban). Az apszisok értékeit gyakran az adott égitest felszínétől adják meg, miközben a legtöbb egyenlet számára a tömegközépponttól számított távolsággal dolgozik, így ilyenkor a felszíntől számított értékekhez hozzá kell adni a test sugarát.
- Peri-* és Apo-*
- Mikor pályákról beszélünk, gyakran a "periapszis" és "apoapszis" módosulnak a pálya közepén lévő égitest nevével. Például, -kee és -kerb mind gyakran használtak a Kerbin körüli pályák leírásakor, minek folytán Perikee/Perikerb és Apokee/Apokerb kifejezésekkel is találkozhatunk.
- Felszálló csomó [Ascending node]
- Az a pont (pályacsomó) amelynél a pálya észak felé haladva metszi a referenciasíkot. Itt, "észak" a referenciasík normálisát jelenti.
- Leszálló csomó [Descending node]
- Az a pont (pályacsomó) ahol a a pálya délfelé haladva metszi a referencia síkot.
- Excentricitás avagy a pálya elnyújtottsága [Eccentricity]
- Egy skalár amely kifejezi a pálya körtől való eltérését .
- ecc = 0 → kör pálya.
- 0 < ecc < 1 → elliptikus pálya.
- ecc = 1 → parabolikus pálya - ez szökési pálya.
- ecc > 1 → hiperbolikus pálya - ez is szökési pálya.
- Inklináció avagy pályahajlás [Inclination]
- A pályasík és a referenciasík által bezárt szög. (megjegyzés az egyenlítő síkjával 90°-ot bezáró pályát poláris-nak nevezik)
- Alacsony pálya [Low orbit]
- Egy stabil és biztonságos keringési pálya amely csak éppen annyira magas, hogy elkerülje a veszélyeket, mint a légkörben való lefékeződést vagy éppen a hegyeknek való ütközést. Az alacsony pálya egy lépcsőfok amely a felemelkedés után várakozhatunk, hogy egy gyorsítással találkozhassunk egy másik járművel vagy égitesttel, vagy éppen az ellenkező irányban a legkevesebb üzemanyag felhasználásával szállhassunk le. A légkörrel rendelkező égitestek esetén, mint amilyen a Kerbin ez a közvetlenül a légkör feletti részt jelenti (70km-100km). A légkör nélküli égitesteknél ez elméletileg bármely felszín feletti magasság lehetne, de egy magasság alatt már a hegyek és magaslatok veszélyeztetik a pályát. Ilyenkor nem árt tudni a magaslatokról! Az időgyorsítás [time warp] korlátozva van az alacsony pályán, és lehetetlen az alatt.
- Pályacsomó (csillagászati definíció)
- Egy pont ahol a pálya keresztezi a referenciasíkot. A felszálló csomó esetében a test a referenciasík pályanormálisának irányában halad. A felszálló irány "észak", míg a leszálló irány "dél" felé mutat.
- Pályacsomók [Orbital nodes] (a játékban)
- Bármely pályán lévő specifikus referenciapontok mint az Apoapszis, Periapszis, vagy a más pályákkal való metszéspontok [intersect points].
- Pályanormális [Orbit normal]
- A pályasík normálisa. Ezt a hajó sebességének és az égitest gravitációjának a vektoriális szorzata adja. Mivel ez a jobb-kéz szabályt követi, olyan nézőpontból, ahonnan a hajó pozitív(az órajárással ellentétes) irányba kering felfelé(a szemlélő felé), ellenkező esetben pedig lefelé(a szélélőtől el) fog mutatni. A "Fel" ["Up"] gyakran mint "észak" [North] or "N+", és a párja mint "Le" ["Down"] másként "Anti-Normál" ["Anti-Normal"] avagy "Dél" ["South"] vagy "N-" van jelölve.
- Pályasík [Orbital plane]
- Egy sík, melyet a keringés pályája feszít ki.
- Pályasebesség [Orbital speed]
- Egy test pályasebessége az a sebesség amellyel a vizsgált rendszer középpontja körül kering, általában egyszerűen nézve a nagyobb test körül. A pályasebességet lehet értelmezni mint átlag-pályasebességet, amellyel megteszi a körülkeringést, vagy a sebesség a pálya egy adott pontján.
- Prográd [Prograde]
- Az az irány amely felé a test halad a pályája mentén. Elliptikus pálya esetén ez mindig a test tartózkodási helyén vett érintő iránya. Menetirányt.
- Retrográd [Retrograde]
- A prográd ellentetje, a pályán haladási iránnyal szemben. Menetiránnyal szemben.
- Referenciasík [Reference plane]
- Bármely sík, amelyet az aktuális pálya leírásakor viszonyítási alapként felhasználunk. A bolygók körüli pályák esetén ez többnyire az egyenlítő síkja. Több test esetén az ellipszis síkját használhatják. Egy másik keringő test befogása esetén a befogandó test pályasíkját használják. Egy pályasíkot teljesen leír egy referenciasíkhoz viszonyított pályahajlás és a felszálló csomó hosszúsági szöge [longitude].
- Fél nagytengely [Semi-major axis]
- → Lásd még: “Fél nagytengely” bekezdést a következő cikkből: Keringési pálya
- A nagy tengely a hosszú tengelye az ellipszisnek a fél nagytengely (a) ennek a fele. Az apoapszis (Q) és a periapszis (q) átlagját középponthoz viszonyítva számítjuk. Mivel mindkettő a felszínhez viszonyított érték, egyszerűen hozzáadjuk az égitest sugarát (R). Egy égitest körül minden azonos fél nagytengellyel rendelkező pályának azonos keringési ideje van, függetlenül az excentricitástól.
- Csillagászati keringési idő [Sidereal period]
- A csillagászati keringési idő (gyakran csak mint keringési idő, de ismert mint sziderikus keringési idő is) az az időciklus amely alatt a keringő test megtesz egy teljes körülkeringést a csillagokhoz viszonyítva. Ezt a keringési ciklust egy inerciarendszerhez (amely nem forog) viszonyítjuk.
- Szuborbitális [Sub-orbital]
- Olyan pálya, amelynél a periapszis az égitest felszíne alatt található. A szuborbitális pályát követve a keringő test szükségszerűen beleütközik az égitestbe.
- Szinodikus keringési idő [Synodic period]
- A szinodikus keringési idő az az időtartam, amennyi ideig tart, hogy egy test újra megjelenjen egy két vagy több testhez viszonyított ugyanazon ponton, pl. a Mün helyzete a Kerbolhoz képest ahogy a Kerbin-ről figyelve visszatér ugyanarra a megvilágítási helyzetbe (holdtölték közti idő). A szinodikus keringési idő az az idő amely eltelik két egymást követő Kerbol–Kerbin vonallal azonos sorrendben történő találkozás (együttállás) között. A szinodikus keringési periódus különbözik a csillagászati keringési periódustól, mivel maga a Kerbin is kering a Kerbol körül.
Hajó irányultsága [Ship Orientation]
A hajó irányultsága mindig egy kiválasztott testhez kötődik. Ez többnyire a kabin.
- Zenit [Zenith]
- A teteje a hajónak többnyire az égitesttől elfelé mutat. A nadír ellentettje.
- Nadír [Nadir]
- Alja a hajónak, általában az égitest felé mutat. A zenit ellentettje.
- Baloldal [Port(side)]
- Bal oldala a hajónak. A jobboldal ellentettje .
- Jobboldal [Starboard]
- Jobb oldala a hajónak. A baloldal ellentettje.
- Eleje [Front]
- Elülső oldala a hajónak, amely többnyire az orr iránya és prográd mutat. A hátulja ellentettje.
- Hátulja [Aft]
- Hátsó oldala a hajónak, mely többnyire a főrakéták otthona és retrogád mutat. Az eleje ellentettje.
Pályamódosítások [Space Maneuvers]
- Levegőfékezés avagy légköri fékezés [Atmospheric braking] [Aerobraking]
- → Főcikk: Levegőfékezés
- Egy égitest felső-légkörébe lépve a légellenállás segítségével az űreszköz veszít a mozgási energiájából, aminek következtében a sebességcsökkenés mellett a hiperbolikus pályagörbén érkező eszköz elliptikus pályára állhat, illetve az elliptikus pályán keringő test apoapszisa is csökken - kisebb értékben a periapszisa is. Okosan alkalmazva a pályamódosítások során ezzel a manőverrel jelentős mértékben csökkenthető az üzemanyag-felhasználás. Viszont ez az alsóbb légkörbe való belépéshez is vezethet, amely során a jelentős lassulás végül az égitestre kényszeríti az eszközt. Ügyelni kell a manőver során, hogy a légellenállás során a súrlódás miatt keletkező hő és erőhatások ne károsítsák az eszközt (A KSP-ben Jelenleg csak DRE mod esetén)!
- Belépés a légkörbe [Atmospheric entry]
- → Főcikk: Belépés a légkörbe
- A légkörbe való belépéskor a légellenállást felhasználva felszínt keresztező pályára lassítjuk az eszközt. Ez jelentős mechanikai- és hőterhelést jelent az eszköz számára, amely az eszköz szétszakadásához, vagy túlhevüléséhez [overheat] vezethet. Túl kis belépési szög esetén az eszköz visszapattan a légkörről a világűrbe (nincs megvalósítva, nincs mod). A légkörbe való belépést gyakran gyakran mint visszatérés a légkörbe vagy egyszerűbben visszatérés [re-entry/reentry] említik, de ez elméletben csak Kerbin atmoszférájába való visszatérésnél igaz (és feltéve, ha nem idegenek lépnek a kis zöld barátaink légkörébe); A légörbe való belépés általánosabb kifejezés.
- Gyorsítás avagy égetés [Burn]
- A hajtóművek használata, általában a pályamódosítás céljából.
- Körpályára állás [Circularizing]
- Egy manőver, melynek során az elliptikus pályát kör alakúra módosítjuk, azaz a pálya excentricitását 0, vagy legalábbis közel 0 szintre csökkentjük. Ezt általában az apszisoknál történő gyorsítással lehet elérni.
- Hintamanőver, gravitációs parittya [Gravity assist]
- → Főcikk: Hintamanőver
- Olyan manőver, amelynél a keringő égitest tömegvonzását használjuk ki a pályamódosításhoz vagy az űrjárművünk sebességének üzemanyag-takarékos megváltoztatására, ezzel jelentős (több száz m/s-nyi Δv) megtakarítást érve el. Az elve szerint gyorsításnál a keringő test mögé, lassításkor a keringő test elé kell célozni.
- Földfékezés [Lithobraking]
- → Lásd még: Földfékezés
- Olyan leszállási manőver, amelyben a leszállás kis szögben történik és légzsákkal védve a leszálló eszközt az kigurulva veszti el a sebességét. Bizonyos estekben a kifejezést az eszköz felszínhez csapódásával történő szándékos megsemmisítésére is használják. Az angol nyelvű elnevezés aerobraking-ből lett ferdítve, ahol areo lecserélték a görög lithos szóra amely követ jelent.
- Manővercsomó [Maneuver node]
- → Főcikk: Manővercsomó
- A manőver csomók kellemes eszközei a pályamódosítások megtervezésének és végrehajtásának, mivel a manőver megkezdése előtt láthatóvá válik az adott gyorsítással létrejövő pályamódosulás.
- Sugárirányú gyorsítás [Radial burn]
- → Lásd még: Manővercsomó
- Sugárirányú befelé gyorsítás [Radial-in burn]
- Az égitest középpontja felé történő gyorsítás. Elfogatja a pályát a keringés irányába amíg a periapszis nem éri el az égitest tömegközéppontját. A sugárirányú kifelé gyorsítás ellentettje.
- Sugárirányú kifelé gyorsítás [Radial-out burn]
- Az égitest középpontjától kifelé történő gyorsítás. Elfogatja a pályát a keringés iránnyal ellentétesen amíg a periapszis át nem halad tömegközéppontján. A sugárirányú befelé gyorsítás ellentettje.
- Visszatérés [Re-entry]
- → Lásd még: Belépés a légkörbe
- Lassítás avagy ellenégetés [Retroburn]
- Olyan gyorsítás amelyet "visszafelé"[backwards] hajtanak végre, azaz a hajtóművek prográd az orr pedig retrográd néznek. Ez az egyszerű manőver a csökkenti pálya magasságát, miközben a pálya egyéb paramétereit nem befolyásolja.
Fizika
- Gyorsulás [Acceleration]
- A sebességváltozás gyorsasága. A gyorsulás vektor jellegű mennyiség, mértékegysége: m/s2.
- Ballisztikus pálya [Ballistic trajectory]
- Egy zuhanó test pályagörbéje ballisztikus. Ez lényegében annyit tesz, hogy az adott testre lényegében csak a gravitáció ereje hat és nincs kitéve egyéb erőknek, mint amilyen a saját hajtómű vagy fékernyő jelentenének.
- Delta-v (Δv)
- A sebességváltozás mértéke amelyet a saját készletéből egy impulzus elven működő jármű képes végrehajtani. Ez sebesség jellegű mennyiség, amely mértékegysége: m/s. A több teher csökkenti a delta-v-t, míg a több üzemanyag növeli. Ez hasznos, mikor egy jármű hatékonyságát akarjuk számolni és jellemezni. Például egy Kerbál Ürközpont kilövőállásáról [Launch pad] indított járműnek mintegy 4500 m/s-nyi delta-v-re van szüksége ahhoz, hogy biztonságosan kilépjen a Kerbin légköréből és stabil pályára álljon a bolygó körül.
- definíciószerűen:
- ahol T az aktuális tolóerő [thrust] m az aktuális tömeg [mass]
Ha feltételezzük, hogy nincs külső erő, és nem váltunk irányt, akkor sebességkülönbséget kapunk:
Ha ezt a fajlagos impulzussal fejtjük ki akkor az eredmény:
- Energia [Energy]
- → Lásd még: Specific orbital energy on Wikipedia
- A keringő test energiája a helyzeti(potenciális) és mozgási(kinetikus) energiájának az összege.
A helyzeti energia: és a mozgási energia:
ahol a G a gravitációs állandó [gravitational constant], M a égitest [celestial body] tömege, m a keringő űrjármű [craft] tömege, R a tömegközéppontjaik közötti távolság és is v a sebesség.
Ez szerint a teljes energia:
Ez az összeg nem változik, ha nincs légellenállás vagy nem működnek a hajtóművek: A periapszis felé haladva helyzeti energia mozgási energiává alakul át, a periapszison áthaladva pedig mozgási energia alakul vissza helyzeti energiává. Ha az energia vagy a fajlagos pályaenergia pozitív, akkor a test szökési pályagörbén van.
- Ez az alaptézise a Kepler-féle bolygómozgás törvénynek, amely alapja a KSP közelítő módszerének. Egy ellipszis olyan pontok halmaza amelyeknek két adott ponttól - a fókuszoktól - vett távolságok összege állandó. Az egyik fókusza a Kepler-pályának a körülkeringett test tömegközéppontja, ahogy egy test megközelíti, az a helyzeti energiáját mozgási energiára váltja. Ahogy a test távolodik a körülkeringett testtől, mivel elliptikus pályáról van szó, ugyanilyen mértékben közelíti meg a másik fókuszt, ezzel a mozgási energiáját helyzeti energiára váltja. Ha a jármű egyenesen az égitest felé vagy felől halad, a fókuszok egybeesnek az apszispontokkal, ahol a mozgási (apoapszis) vagy helyzeti (periapszis) energia nulla. Ha a pálya tökéletes kör (mint a Mün pályája a Kerbin körül), a két fókusz egybeesik és a tengelyek helye határozatlan, mivel a pálya minden pontja apszisnak vehető.
- Van a fajlagos pályaenergia () mely nem igényli a jármú tömegének ismeretét:
, ,
Minden azonos fél nagytengellyel(a) rendelkező pályának azonos a fajlagos pályaenergiája.
- Szökési sebesség [Escape Velocity]
- Az a sebesség, mely egy adott égitest felszínéről indulva a gravitációs hatásának legyőzéséhez szükséges.
Meghatározható:
ahol a G is the gravitációs állandó, M az égitest tömege, r az adott égitest sugara.
- g-erő avagy g-hatás [g-force] (g)
- A gyorsulás értékét a Föld tengerszinten vett nehézségi gyorsulásának értékével kifejezve. 1 g hozzávetőleg 9,81 m/s². Egy test a Föld felszínén 1 g gyorsulásnak megfelelő hatást szenved el. A test súlya duplája 2 g gyorsulásnál és súlytalan 0 g gyorsulás esetén. Szabad esésben, mint mint amilyen a keringési pályán van légellenállás és hajtómű használata nélkül nem tapasztalható gyorsulás, amit úgy fejezhetünk ki, hogy 0 g.
- Gravitáció avagy tömegvonzás [Gravity]
- Minden egyes test tömegéből származó erőhatás. Roppant gyenge. Többnyire csak nagyon nagy tömegű testek mint csillagok, bolygók és holdak fejtenek ki érezhető hatást vele. Az erőhatás nagysága a tömegközéppontól számított távolság négyzetével arányosan csökken. Azaz egy kétszer távolabbi testre 1/22 = 1/4 gravitációs erő hat.
- Gravitációs mező [Gravity Well]
- Az égitest körüli annak gravitációs hatása alatt álló tér. Lényegében a végtelenségig tart, de a gravitáció a távolsággal négyzetesen csökken (kétszeres távolságra a gravitáció csak negyede), így csak a hatásgömbön belül jelentős. Valójában a KSP nem szimulálja a gravitációt az égitestek hatásgömbjén kívül, mivel "foltozott kúpos közelítés"-t használ.
- Keringési pálya avagy pálya [Orbit]
- → Főcikk: Pálya
- Ha egy testnek elégséges tangenciális sebessége van (és a légkörön kívül, hogy a légellenállás nem fékezheti le), akkor az a folytonosan a bolygó "mellé" esik és így sose ér földet akkor ezt a pályagörbét orbitális pályának, vagy röviden pályának nevezzük. A stabil keringési pályák elliptikusak (a kör egy nulla excentricitású ellipszis). Ha a test tangenciális sebessége meghaladja a szökési sebességet a pálya hiperbolikus lesz (határértéken parabolikus).
- Fajlagos impulzus [Specific Impulse] (Isp)
- → Főcikk: Fajlagos impulzus
- Az Isp kifejezi egy impulzus elven működő hatómű hatékonyságát. A magasabb Isp nagyobb fajlagos lendületváltozást azaz sebességváltozást ér el azonos tömegű üzemanyag felhasználásával. A Isp mértékét többnyire másodpercben adják meg ("s"), de fizikailag helyes mértéke a "távolság/idő" amely mértékegysége a m/s. A sebesség mértékéből származó zavart elkerülendő a fizikailag helyes Isp ("távolság/idő")-t elosztották a Föld felszíni nehézségi gyorsulásával (9,81 m/s²). Az eredmény "másodperc" ["second"] mértékegységű. Hogy használhassuk ezt a Isp az egyenletekben, vissza kell alakítanunk "távolság/idő" mértékegységűvé a Földi felszíni gyorsulással való beszorzással. Mivel itt a felszíni gyorsulással való szorzás csak a két mértékegység közti átváltásra szolgál a fajlagos impulzus független a gravitáció aktuális nagyságától.
- Mivel a fajlagos impulzus a tolóerő és a fajlagos üzemanyagfelhasználás hányadosa néha a következő mértékegységben adják meg:
Ez matematikailag egy másik formája a -nak mivel az erő a tömeg és a gyorsulás szorzata Így valójában egyszerű az SI alapegységekkel kifejezve.
- Hatásgömb, hatássugár, vonzáskör [Sphere of influence]
- → Főcikk: Hatásgömb
- Az a tér illetve sugár az égitest körül, amelyen belül az adott égitest gravitációs hatása a meghatározó. Jelölése: SoI/SOI.
- Érintőirányú sebesség [Tangential velocity]
- A sebesség azon komponense, amelyik érintőirányú a pályagörbére. Pillanatnyi sebesség - az a sebesség amikor a mérési idő a nullához közelít - Ez mindig érintőleges a pályagörbére.
- Tolóerő–súly arány [Thrust-to-weight ratio]
- → Főcikk: Tolóerő-súly arány
A jármű/fokozat aktuális tömegének és a rendelkezésre álló tolóerő aránya. Ha a tolóerő–súly arány (TWR) nagyobb mint 1, akkor a járműnek elég tolóereje van hogy felfelé gyorsulva növelje a magasságát. Az 1 alatti tolóerő–súly arány (TWR) a jármű nem tud a gravitáció ellenében haladni alacsony magasságnál, viszont az űrben mindössze hosszabb ideig tartó manővereket jelent. Mivel a súly(W) függ az égitest gravitációjától (g) a tolóerő–súly arány (TWR) függ az adott égitesttől. A felszíni gyorsulás a Mün felszínén mindössze 16,6%-a Kerbinének, így a felszínen a tolóerő–súly arány: TWRKerbin = 1-ről TWRMün = 6-ra változik.
- Pályagörbe [Trajectory]
- A pályagörbe az az útvonal, amelyet a mozgó test az idő függvényében bejár.
- Sebesség [Velocity]
- A helyzetváltozás gyorsasága. A sebesség vektor jellegű mennyiség, azaz van mértéke és iránya. Mértékegysége: m/s.
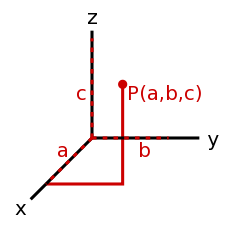
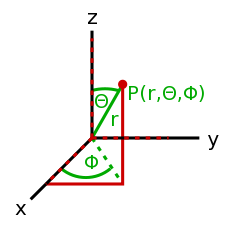














![{\displaystyle [I_{sp}]={\frac {m}{s}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/072515563895cdf8f2d19f1dab433618230ce14f)




