Atmosphere/hu

A légköri nyomások összevetése

Bolygók				Holdak
	Eve		Kerbin		Laythe
	Duna		Jool

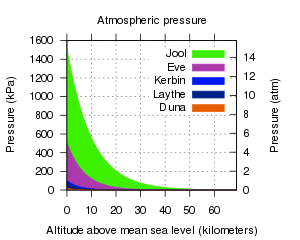
Az égitestek légköre [atmoshpere] fékez minden egyes testet, amely benne halad, az ellenállási erőt amely ilyenkor keletkezik légellenállásnak[atmospheric drag] nevezzük. A légkör lehetővé teszi az aerodinamikus emelést is. A légkörrel rendelkező égitestek rendszerint bolygók, mint az Eve, Kerbin, Duna vagy a gázóriás Jool, de a Laythe, a Jool holdja. Csak a Kerbin és a Laythe légköre tartalmaz számottevő mennyiségben oxigént.

A légnyomás exponenciálisan csökken a magasság függvényében. Egy légkör léptékmagassága az a magasságkülönbség, amelyen a légnyomás a e, avagy 2,718-ed részére csökken. Például a Kerbinnél ez az érték 5 000 m, ez azt jelenti, hogy egy adott magasságon a légnyomás 2,718-szor nagyobb, mint 5 000 m-rel magasabban. Mivel az exponenciális függvény értelmezési tartománya végtelen, a játékban a légkör magassága egy vágási szintet jelent, amely felett a légnyomás teljesen 0, azaz ez a világűr határa. A valós világunkban ezt lényegében a Kármán-vonaltól számítják.

A légkörben a magasság függvényében változik a hőmérséklet is.

A légkör megengedi az üzemanyag-takarékos levegőfékezést és könnyen végrehajtható ejtőernyős leszállást. Ha a légkör elegendő oxigént tartalmaz, akkor akár sugárhajtóműveket is használhatunk. Ellenben a légkör megnehezíti a felszállást, mivel légellenállást generál, rontja a rakétahajtóművek hatékonyságát és lényegesen megnöveli a stabil keringési pálya magasságát.

Légellenállás [Drag]

A Mk1-2 kabin egy Mk16-XL ejtőernyő által keltett légellenállás segítségével fékeződik a Kerbin légkörében.

A légellenállást [Drag] (F_D) a következőképpen írhatjuk le:

$F_{D}=0,5\,\cdot \rho \,\cdot v^{2}\,\cdot C_{w}\,\cdot A$

Ahol ρ a levegő sűrűsége (kg/m³), v a közegben haladó test sebessége (m/s), C_w a légellenállási tényező (dimenziótlan), és az A a homlokfelület (m²).

Az egyenlet első része a dinamikus nyomás [dynamic pressure], jelölése nagybetűs "Q", ami megadja az aerodinamikai hatások nagyságát:

$Q=0,5\,\cdot \rho \,\cdot v^{2}\,$

A levegő sűrűsége ρ állandó összetételt és hőmérsékletet feltételezve arányos a légnyomással (p mértékegysége atm), amely a "tengerszint" feletti magasság [altitude] függvénye. Ha a légnyomás a tengerszinten (0 méteren) (p₀), és a léptékmagasság (H) a Kerbin estében:

${\begin{aligned}p&=p_{0}\cdot e^{\frac {-altitude}{H}}\\\rho &=1,2230948554874{\frac {\text{kg}}{{\text{m}}^{3}\cdot {\text{atm}}}}\cdot p\end{aligned}}$

Ahol a p mértékegysége atm, and ρ pedig kg/m³. Az átváltási tényez ekkor 1,2230948554874 kg/(m³·atm).

Megjegyzés: a régi (1.0 előtti) kiadásokban a FAR kiegészítő segítségével lehetett a valósághű aerodinamikát elérni, az alapjátékban a légellenállási tényező az alkatrészek veleszületett légellenállási tényezőinek tömeggel súlyozott átlaga, ami FlightGlobals API sajátossága volt!
A homlokfelület esetén a játék a következő egyszerűsítéssel élt:

$A=0,008\cdot m$

ahol m a tömeg (kg).

Esési sebesség [Terminal velocity]

A légkörben eső testek esési sebessége az a végsebesség, amelynél a légellenállás és a tömegvonzás kiegyenlíti egymást. A végsebesség egy adott égitesten belül is változik, mivel a légköri jellemzők a szintmagasság függvényei. Elég idő elteltével az adott zuhanó test felveszik a magassághoz tartozó végsebességet, és azzal a sebességgel folytatják az esést.

A végsebesség fontos, mivel:

1. Leírja a talajtérési sebességet, azaz tervezni lehet az ejtőernyős vagy a fékezőrakétás leszállást.
2. Megmutatja az optimális emelkedési sebességet, melynek segítségével üzemanyag-hatékonyan érhetjük el az alacsony keringési pályát.

A tömegvonzás ereje (F_G):

$F_{G}=m\cdot a=m\cdot {\frac {GM}{r^{2}}}$

Ahol az m a jármű tömege, G is the gravitációs állandó, M az égitest tömege, és az r a középpontól vett távolsága az eső testnek.

A végsebességek meghatározásához fel kell írnunk, ahol a F_G = F_D:

${\begin{aligned}m\cdot {\frac {GM}{r^{2}}}&=0,5\,\cdot \rho \,\cdot v^{2}\,\cdot C_{w}\,\cdot A\end{aligned}}$

Ez a KSP világában a következőképpen egyszerűsödött az 1.0-ás kiadás előtt:

${\begin{aligned}m\cdot {\frac {GM}{r^{2}}}&=0,5\cdot \rho \cdot v^{2}\cdot d\cdot \left(0,008{\frac {{\text{m}}^{2}}{\text{kg}}}\cdot m\right)\\{\frac {GM}{r^{2}}}&=0,004{\frac {{\text{m}}^{2}}{\text{kg}}}\cdot \rho \cdot v^{2}\cdot d\\v&=v_{T}={\sqrt {\frac {250{\frac {\text{kg}}{{\text{m}}^{2}}}\cdot GM}{r^{2}\cdot \rho \cdot d}}}\end{aligned}}$

Feltéve d=0,2, mely közelítőleg az ejtőernyő nélküli alapeset:

$v_{T}={\sqrt {\frac {1250{\frac {\text{kg}}{{\text{m}}^{2}}}\cdot GM}{r^{2}\,\rho }}}$

Lássunk egy példát a régi kiadásokra: A mellékelt képen látható földet érő Mk1-2 kapszula (tömeg 4, légellenállás 0,2) esetében Mk16 nyitott ernyővel (tömeg 0,3, légellenállás 500):

Először számoljuk ki a teljes ellenállást, ami ugye a tömeggel súlyozott átlag:

${\frac {4\cdot 0,2+0,3\cdot 500}{4+0,3}}=35,07$

a d=35.07, azaz a tengerszinten így alakul az eső test végsebessége:

$v_{T}={\sqrt {\frac {250{\frac {\text{kg}}{{\text{m}}^{2}}}\cdot GM}{r^{2}\,\rho \cdot 35,07}}}$

$\rho =1,2230948554874{\frac {\text{kg}}{{\text{m}}^{3}\cdot {\text{atm}}}}\cdot 1{\text{atm}}\cdot e^{\frac {-0{\text{m}}}{5000{\text{m}}}}$

$v_{T}={\sqrt {\frac {250{\frac {\text{kg}}{{\text{m}}^{2}}}\cdot 6,674\cdot 10^{-11}{\frac {{\text{m}}^{3}}{{\text{kg}}\cdot {\text{s}}^{2}}}\cdot 5,2915793\cdot 10^{22}\operatorname {kg} }{(600000\operatorname {m} )^{2}\cdot 1,2230948554874{\frac {\text{kg}}{{\text{m}}^{3}}}\cdot 35,07}}}=7,56{\frac {\text{m}}{\text{s}}}$

Példák [Examples]

Magasság (m)	vT (m/s)
	Eve	Kerbin	Duna	Jool	Laythe
0	58,385	100,13	212,41	23,124	115,62
100	58,783	101,01	214,21	23,162	116,32
1000	62,494	109,30	231,16	23,508	122,83
10000	115,27	240,52	495,18	27,272	211,77

Megvezetett fizika [On-rails physics]

A megvezetett fizika szerint a magára hagyott eszközzel (a régi kiadásokban 2,25 km-nél, jelenleg 18 km-nél nagyobb távolságban az irányított eszköztől) a következő történik:

• 0,01 atm alatt: nincs légellenállás — a hajó mintha az űrben közlekedne
• 0,01 atm határ felett: az eszköz eltűnik

Az alábbi táblázat mutatja 0,01 atm-ás határt minden légkörrel rendelkező égitest esetén:

Égitest	Magasság (m)
Eve	44 745
Kerbin	25 789
Duna	10 814
Jool	219 397
Laythe	32 755

Légkörmagasság [Atmospheric height]

A légkör magassága az a tengerszint feletti magasságot, ahol a nyomás 1/1 000 000-od (0,0001%) része a tengerszinti(0 m) nyomásnak. Mivel ez függvénye az égitest léptékmagasságának, ezért ez azt jelenti, hogy ez a magassághatár és a határon a nyomás égitestenként változik. Technikailag a Jool légköre alacsonyabban kezdődik, vagy ahogy vesszük magasabb nyomással...

$alt_{\text{légkörmagasság}}=-ln\left(10^{-6}\right)\cdot {\text{léptékmagasság}}$

$p_{\text{légkörmagasság}}=p_{0}\cdot 10^{-6}$

A Kerbin légköre 0,000001 atm végződik és hasonlóan a következőképpen számíthatjuk a többi égitest légkörének magasságát:

$alt_{\text{légkörmagasság (valós)}}=-ln\left({\frac {10^{-6}}{p_{0}}}\right)\cdot {\text{léptékmagasság}}$

Lásd még

• Belépés a légkörbe
• Esési sebesség a wikin (angol)