Atmosphere/hu

A légköri nyomások összevetése

Bolygók				Holdak
	Eve		Kerbin		Laythe
	Duna		Jool

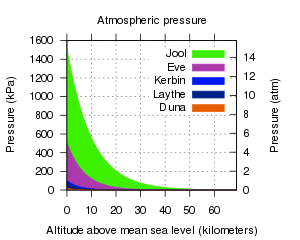
Az égitestek "légköre" lefékez minden egyes testet, amely benne halad, az ellenállási erőt amely ilyenkor keletkezik légellenállásnak[atmospheric drag] nevezzük. A légkör lehetővé teszi az aerodinamikus emelést is. A légkörrel rendelkező égitestek rendszerint bolygók, mint az Eve, Kerbin, Duna vagy a gázóriás Jool, de a Laythe, a Jool holdja. Csak a Kerbin és a Laythe légköre tartalmaz számottevő mennyiségben oxigént.

A légnyomás exponenciálisan csökken a magasság függvényében. Egy légkör "léptékmagassága" az a magasságkülönbség, amelyen a légnyomás a e, avagy 2.718-ed részére csökken. Például a Kerbinnél ez az érték 5000 m, ez azt jelenti, hogy egy adott magasságon a légnyomás 2,718-szor nagyobb, mint 5000m-rel magasabban. Mivel az exponenciális függvény értelmezési tartománya végtelen, a játékban a légkör magassága egy vágási szintet jelent, amely felett a légnyomás teljesen 0, azaz ez a világűr határa. A valós világunkban ezt lényegében a Kármán-vonaltól számítják.

A légkörben változik a hőmérséklet is, bár ez nem számít a játékban

A légkör megengedi az üzemanyag-takarékos levegőfékezést és könnyű ejtőernyős leszállást. Ha a légkör elegendő oxigént tartalmaz, akkor gázturbinás sugárhajtóműveket is használhatunk. Ellenben a légkör megnehezíti a felszállást, mivel légellenállást generál, rontja a rakétahajtóművek hatékonyságát és lényegesen megnöveli a stabil keringési pálya magasságát.

Légellenállás [Drag]

A Mk1-2 kabin egy Mk16-XL ejtőernyő által keltett légellenállás segítségével fékeződik a Kerbin légkörében.

In the game, the force of atmospheric drag (F_D) is modeled as follows:

$F_{D}=0.5\,\rho \,v^{2}\,d\,A$

where ρ is the atmospheric density (kg/m³), v is the ship's velocity (m/s), d is the coefficient of drag (dimensionless), and A is the cross-sectional area (m²).

Note that the cross-sectional area is not actually calculated in the game. It is instead assumed that it is directly proportional to the mass, which is an unrealistic simplification made by KSP. The parameter FlightGlobals.DragMultiplier indicates that the proportionality ratio is 0.008 m²/kg, so:

$A=0.008\cdot m$

where m is the ship's mass (kg).

The atmospheric density ρ is directly proportional to atmospheric pressure (p of unit atm), which is a function of altitude, the atmosphere's pressure at altitude 0 (p₀), and scale height (H):

${\begin{aligned}p&=p_{0}\cdot e^{\frac {-altitude}{H}}\\\rho &=1.2230948554874{\frac {\text{kg}}{{\text{m}}^{3}\cdot {\text{atm}}}}\cdot p\end{aligned}}$

where p here is in units atm, and ρ in kg/m³. The conversion factor of 1.2230948554874 kg/(m³·atm) is given by FlightGlobals.getAtmDensity(1.0), which returns the density at 1 atmosphere (sea level on Kerbin) pressure.

The coefficient of drag (d) is calculated as the mass-weighted average of the max_drag values of all parts on the ship. For most ships without deployed parachutes, d will be very near 0.2, since this is the max_drag value of the vast majority of parts. Also a group of the same part have always the same drag coefficient.

As an example, the coefficient of drag for a craft consisting simply of a Mk1-2 Command Pod (mass 4, drag 0.2) and a deployed Mk16-XL Parachute (mass 0.3, drag 500) is:

${\frac {4\cdot 0.2+0.3\cdot 500}{4+0.3}}=35.07$

Terminal velocity

The terminal velocity of an object falling through an atmosphere is the velocity at which the force of gravity is equal to the force of drag. Terminal velocity changes as a function of altitude. Given enough time, an object falling into the atmosphere will slow to terminal velocity and then remain at terminal velocity for the rest of its fall.

Terminal velocity is important because:

1. It describes the amount of velocity which a spacecraft must burn away when it is close to the ground.
2. It represents the speed at which a ship should be traveling upward during a fuel-optimal ascent.

The force of gravity (F_G) is:

$F_{G}=m\cdot a=m\cdot {\frac {GM}{r^{2}}}$

where m is still the ship's mass, G is the gravitational constant, M is the mass of the planet, and r is the distance from the center of the planet to the falling object.

To find terminal velocity, we set F_G equal to F_D:

${\begin{aligned}m\cdot {\frac {GM}{r^{2}}}&=0.5\cdot \rho \cdot v^{2}\cdot d\cdot \left(0.008{\frac {{\text{m}}^{2}}{\text{kg}}}\cdot m\right)\\{\frac {GM}{r^{2}}}&=0.004{\frac {{\text{m}}^{2}}{\text{kg}}}\cdot \rho \cdot v^{2}\cdot d\\v&=v_{T}={\sqrt {\frac {250{\frac {\text{kg}}{{\text{m}}^{2}}}\cdot GM}{r^{2}\cdot \rho \cdot d}}}\end{aligned}}$

Assuming d is 0.2 (which is a good approximation, provided parachutes are not in use), this simplifies to:

$v_{T}={\sqrt {\frac {1250{\frac {\text{kg}}{{\text{m}}^{2}}}\cdot GM}{r^{2}\,\rho }}}$

For the Mk16 pod and parachute example pictured above, the drag coefficient is 35.07, so its terminal velocity at sea level on Kerbin (which is 600 km from Kerbin's center) is:

$v_{T}={\sqrt {\frac {250{\frac {\text{kg}}{{\text{m}}^{2}}}\cdot GM}{r^{2}\,\rho \cdot 35.07}}}$

$\rho =1.2230948554874{\frac {\text{kg}}{{\text{m}}^{3}\cdot {\text{atm}}}}\cdot 1{\text{atm}}\cdot e^{\frac {-0{\text{m}}}{5000{\text{m}}}}$

$v_{T}={\sqrt {\frac {250{\frac {\text{kg}}{{\text{m}}^{2}}}\cdot 6.674\cdot 10^{-11}{\frac {{\text{m}}^{3}}{{\text{kg}}\cdot {\text{s}}^{2}}}\cdot 5.2915793\cdot 10^{22}\operatorname {kg} }{(600000\operatorname {m} )^{2}\cdot 1.2230948554874{\frac {\text{kg}}{{\text{m}}^{3}}}\cdot 35.07}}}=7.56{\frac {\text{m}}{\text{s}}}$

Examples

Altitude (m)	vT (m/s)
	Eve	Kerbin	Duna	Jool	Laythe
0	58,385	100,13	212,41	23,124	115,62
100	58,783	101,01	214,21	23,162	116,32
1000	62,494	109,30	231,16	23,508	122,83
10000	115,27	240,52	495,18	27,272	211,77

On-rails physics

If a ship is "on rails" (meaning it's further than 2.25 km from the actively-controlled ship) and its orbit passes through a planet's atmosphere, one of two things will happen based on atmospheric pressure at the ship's altitude:

• below 0.01 atm: no atmospheric drag will occur — the ship will be completely unaffected
• 0.01 atm or above: the ship will disappear

The following table gives the altitude of this 0.01 atm threshold for each celestial body with an atmosphere:

Body	Altitude (m)
Eve	0
Kerbin	0
Duna	0
Jool	0
Laythe	0

Légkörmagasság [Atmospheric height]

A légkör magassága függ az égitest léptékmagasságtól, ahol a nyomás 0.000001^th (0.0001 %) része a felszíni nyomásnak, így a határon a nyomás égitestenként változik. Technikailag a Jool légköre alacsonyabban kezdődik, vagy ahogy vesszük magasabb nyomással...

$alt_{\text{légkörmagasság}}=-ln\left(10^{-6}\right)\cdot {\text{léptékmagasság}}$

$p_{\text{légkörmagasság}}=p_{0}\cdot 10^{-6}$

A Kerbin légköre 0.000001 atm végződik és hasonlóan a következőképpen számíthatjuk a többi égitest légkörének magasságát:

$alt_{\text{légkörmagasság (valós)}}=-ln\left({\frac {10^{-6}}{p_{0}}}\right)\cdot {\text{léptékmagasság}}$

Lásd még

• Belépés a légkörbe