Difference between revisions of "Orbit/es"
(Created page with "thumb|right|Una astronave en órbita alrededor de [[Moho/es|Moho.]] Una '''órbita''' es un paso elíptico alrededor de un celestial...") |
|||
| Line 78: | Line 78: | ||
=== Suborbita === | === Suborbita === | ||
| − | Una órbita es una suborbita si el periapsis esta debajo de la superficie, entonces esta no podrá completar una órbita completa sin estrellarse en la superficie o aterrizar. Superficies sustentadoras como las [[wing|alas]] | + | Una órbita es una suborbita si el periapsis esta debajo de la superficie, entonces esta no podrá completar una órbita completa sin estrellarse en la superficie o aterrizar. Superficies sustentadoras como las [[wing|alas]] deberían ralentizar esto. |
| + | |||
| + | == Órbitas en el archivo de guardado == | ||
| + | El archivo de guardado (y escenarios) en KSP son texto plano que los humanos pueden leer con información de la órbita de cada vehículo en el juego. Muchos editores de texto permiten buscar <code>name = [Nombre del vehiculo]</code> via {{Key press|Ctrl|F}} ({{Key press|⌘Cmnd|F}} para Mac). Esto ubica rápidamente el vehículo en el archivo. La sección órbitas de persistent.sfs muestra algo como esto: | ||
| + | |||
| + | ORBIT | ||
| + | { | ||
| + | SMA = 76875.4600066045 | ||
| + | ECC = 0.136808532664149 | ||
| + | INC = 32.6082297441138 | ||
| + | LPE = 91.4665699628126 | ||
| + | LAN = 305.802690796769 | ||
| + | MNA = 0.556028537338098 | ||
| + | EPH = 19189976.1161395 | ||
| + | REF = 3 | ||
| + | OBJ = 0 | ||
| + | } | ||
| + | |||
| + | Cada uno de estos términos tiene un significado físico y juntos definen una órbita. Cambiándolos (y recargando el juego salvado) cambiara la órbita del vehículo en cuestión. | ||
| + | |||
| + | Los primeros cinco parámetros son únicamente para definir una trayectoria Kepleriana: | ||
| + | * '''Excentricidad''' (ECC) and '''Semieje Mayor''' (SMA) especifican, respectivamente, la forma de la trayectoria (0 = circular, < 1 = elíptica, 1 = parabólica, > 1 = hiperbólica) y su tamaño (La mitad de la distancia entre el periapsis y el apoapsis, o equivalentemente el promedio de estos medidos desde el centro del cuerpo). Las órbitas hiperbólicas tienen un “semieje mayor” negativo que esta relacionado con la definición matemática de una hipérbola como un par de curvas simétricas, de las cuales la órbita es una rama. Sin embargo, debido a el sistema de esferas de influencia de KSP, un objeto puede tener una órbita elíptica (semieje mayor positivo y excentricidad debajo de 1) y aun puede estar escapando. | ||
| + | * '''Inclinación''' (INC) y '''longitud del Nodo Ascendente''' (LAN) especifican la inclinación del plano orbital (En sentido anti-horario desde la eclíptica en el nodo ascendente) y su orientación (En sentido anti-horario desde el punto vernal hasta el nodo ascendente). En la Tierra, el punto vernal es el punto donde el Sol esta en el equinoccio de verano en el hemisferio norte (El nodo ascendente de la eclíptica al ecuador celeste). Como Kerbin no tiene inclinación axial, el punto vernal es arbitrario. | ||
| + | * '''Longitud del Periapsis''' (LPE) especifica la orientación de la órbita con su plano (En sentido anti-horario desde el nodo ascendente al periapsis). | ||
| + | Entonces la posicion del objeto en la orbita en cierto tiempo es extrapolada de: | ||
| + | * '''Epoca''' (EPH), una referencia de tiempo, y | ||
| + | * '''Anomalia Media a la epoca''' (MNA), un pseudo-angulo (hasta 2π) expresando la proporción de periodo orbital que ha pasado desde el ultimo periapsis. Este es el angulo de la correspondiente posición en una órbita circular. Para las órbitas hiperbólicas este es negativo acercandoce al periapsis y positivo alejándose de el. | ||
| + | Estos números son para ponerse en contexto: | ||
| + | * REF : un numero de referencia que se da al cuerpo al cual se esta orbitando. Ver abajo por la tabla. | ||
| + | * OBJ : algún tipo de referencia de objeto (Yo no he cambiado este numero). Posiblemente un código para el icono mostrado - parece que 0 corresponde a satélites, y 1 corresponde a escombros. | ||
| + | |||
| + | Los ángulos están algunos en radianes (MNA) y otros en cegesimales (INC), las distancias esta en metros. | ||
| + | |||
| + | Alterando estos valores en el archivo de guardado es fácil colocar los vehículos en cualquier posición deseada. Esto es muy útil para armar escenarios. | ||
| + | |||
| + | === Reference code === | ||
| + | Esta tabla contiene los códigos de referencia para todos los cuerpos en el [[Kerbol System|Sistema Kerbol]]: | ||
| + | {| class="wikitable" | ||
| + | ! colspan="2" | Planetas/Estrellas | ||
| + | ! colspan="2" | Lunas | ||
| + | |- | ||
| + | ! Código | ||
| + | ! Nombre | ||
| + | ! Código | ||
| + | ! Nombre | ||
| + | |- | ||
| + | | 0 | ||
| + | | [[Kerbol]] | ||
| + | |- | ||
| + | | 4 | ||
| + | | [[Moho]] | ||
| + | |- | ||
| + | | 5 | ||
| + | | [[Eve]] | ||
| + | | 13 | ||
| + | | [[Gilly]] | ||
| + | |- | ||
| + | | rowspan="2" valign="top" | 1 | ||
| + | | rowspan="2" valign="top" | [[Kerbin]] | ||
| + | | 2 | ||
| + | | [[Mun]] | ||
| + | |- | ||
| + | | 3 | ||
| + | | [[Minmus]] | ||
| + | |- | ||
| + | | 6 | ||
| + | | [[Duna]] | ||
| + | | 7 | ||
| + | | [[Ike]] | ||
| + | |- | ||
| + | | 15 | ||
| + | | [[Dres]] | ||
| + | |- | ||
| + | | rowspan="5" valign="top" | 8 | ||
| + | | rowspan="5" valign="top" | [[Jool]] | ||
| + | | 9 | ||
| + | | [[Laythe]] | ||
| + | |- | ||
| + | | 10 | ||
| + | | [[Vall]] | ||
| + | |- | ||
| + | | 12 | ||
| + | | [[Tylo]] | ||
| + | |- | ||
| + | | 11 | ||
| + | | [[Bop]] | ||
| + | |- | ||
| + | | 14 | ||
| + | | [[Pol]] | ||
| + | |- | ||
| + | | 16 | ||
| + | | [[Eeloo]] | ||
| + | |} | ||
| + | |||
| + | == Referencias == | ||
| + | <references /> | ||
| + | |||
| + | == Enlaces externos == | ||
| + | * {{Wikipedia}} | ||
| + | * {{Wikipedia|Apsis}} | ||
| + | * {{Wikipedia|Low Earth orbit}} | ||
| + | * Kraft, D and Townsend, G. (1963). ''NASA Orbital Flight Handbook, Part 1 - Basic Techniques and Data''. Space Flight Handbooks, Vol. 1. http://ntrs.nasa.gov/search.jsp?R=19630011221 | ||
| + | ** Para una enorme tabla de ecuaciones Keplerianas, ve el pdf en la pagina 126/III-16. | ||
Latest revision as of 03:39, 6 January 2017
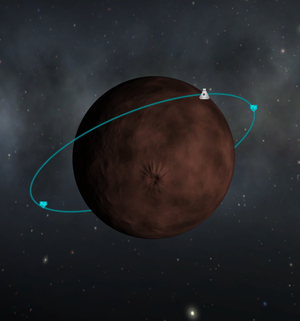
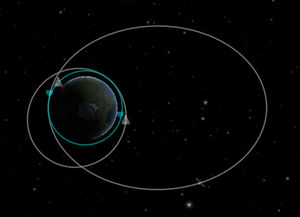
Una órbita es un paso elíptico alrededor de un cuerpo celeste. El punto de la órbita que se encuentra mas cerca del cuerpo orbitado se llama periapsis y el punto más lejano se llama apoapsis. Estos puntos son indicados en el mapa como "Pe" y "Ap", respectivamente.
Una órbita es considerada “estable” si todos los puntos de la órbita están sobre el terreno y la atmósfera del cuerpo orbitado, esto aplica si el periapsis esta ubicado fuera del terreno y la atmósfera del cuerpo orbitado al ser este el punto mas bajo de la órbita. Una astronave en estas órbitas no perderá velocidad por el roce atmosférico y no colisionara con el terreno.
Para alcanzar una órbita, una astronave debe conseguir suficiente velocidad orbital y altitud. Durante el ascenso, una asistencia gravitatoria ayuda a conseguir estos objetivos en una manera eficiente y con poco uso de combustible. Con maniobras básicas es posible cambiar la forma de la órbita.
Contents
Propiedades
Cada órbita posee propiedades básicas que la caracterizan. Esta lista contiene múltiples elementos que pueden ser calculados usando otras propiedades de la lista.
Apoapsis y periapsis
- → Ver también: Apsis on Wikipedia en ingles
El periapsis y el apoapsis son el punto mas cercano y mas lejano de la órbita respectivamente. El periapsis es el punto mas bajo de la órbita y ayuda bastante para determinar si la órbita es suficientemente alta para evitar colisiones con la superficie o interactuar con la atmósfera. El apoapsis esta al otro lado de la órbita y es el punto mas lejano del cuerpo orbitado. El periapsis no es mostrado si este esta por debajo de la superficie. Hay una gran confusión sobre desde donde el apoapsis y el periapsis son medidos. En el juego son medidos desde la superficie, mientras que para la mecánica de las órbitas los valores desde el centro del cuerpo son relevantes.
Para las trayectorias parabólicas e hiperbólicas, no existe el apoapsis y la curva que describe es abierta. El apoapsis y el periapsis en otras esferas de influencia son posibles. El periapsis de tal trayectoria solamente es mostrado si existe en el futuro, y tan pronto como la nave pases por el periapsis y comience a elevarse, este desaparecerá.
En una órbita circular perfecta es imposible determinar el periapsis y el apoapsis. La altura, que es igual en toda la órbita, es requerida para ello. Estos son idénticos al semieje mayor cuando son medidas desde el centro. Las órbitas elípticas tienen usualmente periapsis y apoasis, aunque algunas veces no tienen periapsis ya que este se esconde debajo de la superficie. Si una órbita es casi circular esta es tratada como perfectamente circular donde el semieje mayor, el periapsis y el apoapsis son idénticos medidos desde el centro del cuerpo.
Algunas veces palabras especiales son usadas para diferentes cuerpos. Apokee o apokerb se usan para el apoapsis de una órbita alrededor de Kerbin e igualmente perikee o perikerb para el periapsis alrededor de Kerbin.
En Kerbal Space Program, el periapsis y el apoapsis son usualmente abreviados como “Pe” y “Ap” respectivamente. En el mundo científico real una Q mayúscula se usa para el apoapsis y una q minúscula para el periapsis porque las variables usualmente contienen solo una letra. Usar a para el apoapsis no es recomendable ya que podría generar confusión con el semieje mayor que usualmente tiene esta variable.
Excentricidad
- → Ver también: Excentricidad en Wikipedia
La excentricidad dice que tan circular es una órbita. Existen diferentes excentricidades, aunque usualmente la excentricidad orbital is usada para mecánica orbital. Esta puede ser separada en cuatro categorías:
- En una órbita circular la excentricidad es exactamente 0
- En una órbita elíptica la excentricidad esta entre 0 y 1
- En una órbita parabólica la excentricidad es exactamente 1
- En una órbita hiperbólica la excentricidad es mayor que 1
Si la excentricidad es igual o mas grande que 1 la órbita es una órbita de escape del cuerpo. Las órbitas circulares y parabólicas no son comunes sino imposibles, puesto que las maniobras tienen que ser extremadamente precisas. Es posible, sin embargo, obtener una excentricidad muy cercana a 0 o 1 que puede ser considerada como circular o parabólica respectivamente. Algunos planetas y lunas en Kerbal Space Program tienen una órbita circular perfecta porque ellos se mueven por "rieles"; ninguna interacción física puede cambiar sus propiedades.
No obstante, una órbita con una excentricidad menor que 1 puede escapar esfera de influencia Porque la excentricidad esta basada en el periapsis y en el apoapsis; esta no toma en cuenta la distancia restante entre el apoapsis y la esfera de influencia del cuerpo. Una órbita circular cerca de la esfera de influencia tiene una excentricidad 0, pero tan pronto como el apoapsis sea incrementado, la órbita dejara la esfera de influencia, aunque de hecho la excentricidad aun este cerca del 0.
La excentricidad es usualmente abreviada con una e minúscula. Esta puede ser calculada en el juego con (Ap-Pe)/(2R+Ap+Pe), donde Ap is el apoapsis, Pe es el periapsis, y R el radio del cuerpo orbitado.
Inclinación
- → Artículo principal: Inclinación Orbital en Wikipedia
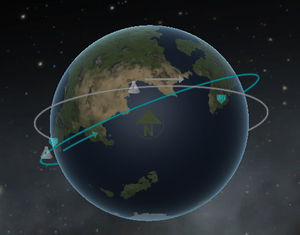
La inclinación esta dada usualmente en grados donde el valor esta dado entre -90° y 270°. Una inclinación de 0° o 180°es ecuatorial, entonces la nave estará siempre sobre el ecuador. Una inclinación de 90° is característica de las órbitas polares. Cuando la inclinación esta debajo de los 90° la órbita es progrado, significa que la rotación alrededor del cuerpo va en el mismo sentido que la rotación del cuerpo. Una inclinación sobre los 90° y debajo de 270° determina una órbita retrogrado, significa que la rotación es en el sentido opuesto. Como todos los cuerpos en el Sistema Kerbol están rotando en sentido anti-horario, visto desde el polo Norte, todas las órbitas progrado van en sentido anti-horario y las órbitas retrogado van en sentido horario.
Dependiendo de la posición inicial la órbita directamente disponible de mas baja inclinación esta limitada por la latitud. Una órbita polar es siempre posible, mientras que para órbitas ecuatoriales la nave tiene que empezar en el ecuador. Como el Centro Espacial Kerbal esta cerca del ecuador es posible lanzarse en todas las inclinaciones sin muchas maniobras orbitales.
Mientras que una órbita polar, dependiendo de la altitud y cobertura cerca de las inclinaciones polares, cubre todo el cuerpo, encontrarse con un objeto en una órbita ecuatorial es mucho más fácil. La inclinación es exactamente el rango de latitudes que una nave puede pasar en ambas direcciones(Norte y Sur).
Actualmente no existe forma directa de determinar la inclinación sin usar mods. para algunos planetas es posible determinar a inclinación si el planeta es orbitado por una luna sin inclinación. La luna puede ser elegida como blanco y el angulo dado por el nodo ascendente y descendente es la inclinación. Esto es posible alrededor de Kerbol. La “luna” sin inclinacion seria Kerbin.
La inclinación esta dada en muchos casos relativa al ecuador del cuerpo orbitado, pero en especial la inclinación del planeta puede ser dada relativa a la eclíptica. La eclíptica es el plano orbital de Kerbin porque la inclinación relativa al ecuador de Kerbol es 0°, es decir no hay diferencia entre la ubicación relativa al ecuador de Kerbol y la eclíptica.
Semieje mayor
- → Ver también: semieje mayor en Wikipedia
El semieje mayor es el promedio entre el periapsis y el apoapsis, usualmente medido desde el centro del cuerpo. El semieje mayor no puede ser medido directamente en el juego sin mods, pero puede ser fácilmente calculado dividiendo la suma de el periapsis y el apoapsis entre dos. El semieje mayor define el periodo orbital, entonces no importa que tan elongada sea una órbita, si el semieje mayor es el mismo el periodo orbital no cambia. Esto hace que las órbitas sincrónica sean mas fáciles de alcanzar, ya que una órbita circular solo es importante para órbitas estacionarias.
Si el apoapsis y el periapsis son dados desde la superficie del cuerpo la misma formula puede ser usada pero al resultado final tiene que añadirse el radio del cuerpo. El semieje mayor puede ser usado como una distancia promedio, pero depende de la definición de lo que distancia promedio significa. En formulas el semieje mayor es usualmente abreviado con una a minúscula, que no debe ser confundida con apoapsis.
Tipos de órbitas
Órbita Baja Kerbin (LKO)
En análogo a la órbita baja terrestre (LEO) en el mundo real, una LKO describe una órbita baja estable alrededor de Kerbin que puede ser alcanzada con un costo relativamente bajo de Delta-V. El punto mas bajo de una LKO no debe ser menor que 70 km para evitar la fricción atmosférica. La altura de una LKO no excede los 200 km.
Toneladas de carga son enviadas a LKO para comparar el rendimiento y el tamaño de los vehiculos de lanzamiento.
En circunstancias optimas una LKO Puede ser alcanzada con 4450–4700 m/s de Delta-V.[1]
Debido al efecto Oberth una órbita baja es un buen punto para realizar una transferencia a otro cuerpo celeste.[citation needed]
Stationary orbit and synchronous orbit
- → Artículo principal: Stationary orbit en ingles
Una órbita con el mismo periodo orbital que el periodo rotacional del cuerpo orbitado es llamada órbita sincrónica. si la inclinación es también 0° y no hay excentricidad es llamada órbita estacionaria. Un satélite en esta órbita parece no moverse cuando es visto desde la superficie del cuerpo.
Orbita Ecuatorial Kerbisincronizada (KEO)
- → Artículo principal: KEO en ingles
La órbita estacionaria alrededor de Kerbin, donde la nave orbitando parece quedarse quieta en un punto sobre el ecuador de Kerbin. El nombre fue escogido para abreviarse de manera similar que GEO la abreviación de Órbita Geoestacionaria, que es el equivalente real en la Tierra.
Otros
Otras órbitas pueden ser definidas. La lista de órbitas (Wikipedia en ingles) Contiene muchos de las mas comunes en la vida real. Estas pueden ser recreadas modificando los fundamentos para encajar en un universo mas pequeño. Alguna clases de órbitas, como la órbita heliosincrona alrededor de la Tierra no son posibles, porque ella requeriría que la gravedad de Kerbin no fuera perfecta. Como los puntos de Lagrange no existen, entonces las órbitas alrededor/cerca de un punto de Lagrange son imposibles. Pero es posible imitar L4 y L5, Aunque cada orbita con el mismo semieje mayor tiene el mismo periodo orbital L4 y L5 no tienen posiciones especiales.
Suborbita
Una órbita es una suborbita si el periapsis esta debajo de la superficie, entonces esta no podrá completar una órbita completa sin estrellarse en la superficie o aterrizar. Superficies sustentadoras como las alas deberían ralentizar esto.
Órbitas en el archivo de guardado
El archivo de guardado (y escenarios) en KSP son texto plano que los humanos pueden leer con información de la órbita de cada vehículo en el juego. Muchos editores de texto permiten buscar name = [Nombre del vehiculo] via ^ Ctrl+F (⌘Cmnd+F para Mac). Esto ubica rápidamente el vehículo en el archivo. La sección órbitas de persistent.sfs muestra algo como esto:
ORBIT
{
SMA = 76875.4600066045
ECC = 0.136808532664149
INC = 32.6082297441138
LPE = 91.4665699628126
LAN = 305.802690796769
MNA = 0.556028537338098
EPH = 19189976.1161395
REF = 3
OBJ = 0
}
Cada uno de estos términos tiene un significado físico y juntos definen una órbita. Cambiándolos (y recargando el juego salvado) cambiara la órbita del vehículo en cuestión.
Los primeros cinco parámetros son únicamente para definir una trayectoria Kepleriana:
- Excentricidad (ECC) and Semieje Mayor (SMA) especifican, respectivamente, la forma de la trayectoria (0 = circular, < 1 = elíptica, 1 = parabólica, > 1 = hiperbólica) y su tamaño (La mitad de la distancia entre el periapsis y el apoapsis, o equivalentemente el promedio de estos medidos desde el centro del cuerpo). Las órbitas hiperbólicas tienen un “semieje mayor” negativo que esta relacionado con la definición matemática de una hipérbola como un par de curvas simétricas, de las cuales la órbita es una rama. Sin embargo, debido a el sistema de esferas de influencia de KSP, un objeto puede tener una órbita elíptica (semieje mayor positivo y excentricidad debajo de 1) y aun puede estar escapando.
- Inclinación (INC) y longitud del Nodo Ascendente (LAN) especifican la inclinación del plano orbital (En sentido anti-horario desde la eclíptica en el nodo ascendente) y su orientación (En sentido anti-horario desde el punto vernal hasta el nodo ascendente). En la Tierra, el punto vernal es el punto donde el Sol esta en el equinoccio de verano en el hemisferio norte (El nodo ascendente de la eclíptica al ecuador celeste). Como Kerbin no tiene inclinación axial, el punto vernal es arbitrario.
- Longitud del Periapsis (LPE) especifica la orientación de la órbita con su plano (En sentido anti-horario desde el nodo ascendente al periapsis).
Entonces la posicion del objeto en la orbita en cierto tiempo es extrapolada de:
- Epoca (EPH), una referencia de tiempo, y
- Anomalia Media a la epoca (MNA), un pseudo-angulo (hasta 2π) expresando la proporción de periodo orbital que ha pasado desde el ultimo periapsis. Este es el angulo de la correspondiente posición en una órbita circular. Para las órbitas hiperbólicas este es negativo acercandoce al periapsis y positivo alejándose de el.
Estos números son para ponerse en contexto:
- REF : un numero de referencia que se da al cuerpo al cual se esta orbitando. Ver abajo por la tabla.
- OBJ : algún tipo de referencia de objeto (Yo no he cambiado este numero). Posiblemente un código para el icono mostrado - parece que 0 corresponde a satélites, y 1 corresponde a escombros.
Los ángulos están algunos en radianes (MNA) y otros en cegesimales (INC), las distancias esta en metros.
Alterando estos valores en el archivo de guardado es fácil colocar los vehículos en cualquier posición deseada. Esto es muy útil para armar escenarios.
Reference code
Esta tabla contiene los códigos de referencia para todos los cuerpos en el Sistema Kerbol:
| Planetas/Estrellas | Lunas | ||
|---|---|---|---|
| Código | Nombre | Código | Nombre |
| 0 | Kerbol | ||
| 4 | Moho | ||
| 5 | Eve | 13 | Gilly |
| 1 | Kerbin | 2 | Mun |
| 3 | Minmus | ||
| 6 | Duna | 7 | Ike |
| 15 | Dres | ||
| 8 | Jool | 9 | Laythe |
| 10 | Vall | ||
| 12 | Tylo | ||
| 11 | Bop | ||
| 14 | Pol | ||
| 16 | Eeloo | ||
Referencias
Enlaces externos
- Orbit on Wikipedia
- Apsis on Wikipedia
- Low Earth orbit on Wikipedia
- Kraft, D and Townsend, G. (1963). NASA Orbital Flight Handbook, Part 1 - Basic Techniques and Data. Space Flight Handbooks, Vol. 1. http://ntrs.nasa.gov/search.jsp?R=19630011221
- Para una enorme tabla de ecuaciones Keplerianas, ve el pdf en la pagina 126/III-16.